序言
在数值计算与优化理论的广阔天地里,梯度作为一阶导数的向量表示,是理解函数局部变化率及进行最优化求解的基础工具。然而,当问题的复杂度提升,单一梯度信息往往不足以全面刻画函数的多变量间相互作用及更高阶的变化特性。此时, Jacobian \text{Jacobian} Jacobian矩阵与 Hessian \text{Hessian} Hessian矩阵便成为不可或缺的数学利器,它们分别扩展了梯度概念至向量值函数与二阶导数领域,为深入探索函数性质、设计高效算法提供了坚实的理论基础。
概述
Jacobian矩阵
- Jacobian \text{Jacobian} Jacobian矩阵是函数值从向量空间到向量空间的线性映射的一阶偏导矩阵,它在多变量向量值函数的微分学中占据核心地位。
- 该矩阵的每一行代表函数输出向量中某一分量对所有输入变量的一阶偏导数,从而全面揭示了输入向量变化时,输出向量如何线性地变化。
- 在机器学习的神经网络中, Jacobian \text{Jacobian} Jacobian矩阵常用于反向传播算法中,帮助计算梯度。
Hessian矩阵
- Hessian \text{Hessian} Hessian矩阵则是函数二阶偏导数的方阵,反映了函数在某一点上的局部曲率信息。
- 它不仅告诉我们函数值如何随单个变量的二阶变化,还揭示了变量间相互作用的二阶效应。
- Hessian \text{Hessian} Hessian矩阵在优化算法中尤为重要,其正定性可用于判断局部极小值点,负定性则指向局部极大值,而零特征值则暗示了可能存在的鞍点或平坦区域。
- 此外, Hessian \text{Hessian} Hessian矩阵还应用于牛顿法等二阶优化算法中,通过直接利用二阶信息加速收敛过程。
数值计算之梯度之上Jacobian和Hessian矩阵
- Jacobian矩阵
-
有时我们需要计算输入和输出都为向量的函数的所有偏导数。包含所有这样的偏导数的矩阵被称为Jacobian矩阵。
-
具体来说,如果我们有一个函数: f : R m → R n \boldsymbol{f}:\mathbb{R}^m\to\mathbb{R}^n f:Rm→Rn, f \boldsymbol{f} f的 Jacobian \text{Jacobian} Jacobian矩阵 J ∈ R n × m \boldsymbol{J}\in\mathbb{R}^{n\times m} J∈Rn×m定义为: J i , j = ∂ ∂ x j f ( x ) i J_{i,j}=\displaystyle\frac{\partial}{\partial x_j}f(\boldsymbol{x})_i Ji,j=∂xj∂f(x)i。
-
Hessian矩阵
-
有时,我们也对导数的导数高兴去,即二阶导数(second derivative)。
-
例如,有一个函数 f : R m → R n f:\mathbb{R}^m\to\mathbb{R}^n f:Rm→Rn, f f f的一阶导数(关于 x j x_j xj)关于 x i x_i xi的导数记为: ∂ 2 ∂ x i ∂ x j f \displaystyle\frac{\partial^2}{\partial x_i\partial x_j}f ∂xi∂xj∂2f。
-
在一维情况下,我们可以将二阶导数: ∂ 2 ∂ x i 2 f \displaystyle\frac{\partial^2}{\partial x_i^2}f ∂xi2∂2f,记为 f ′ ′ ( x ) f''(x) f′′(x)。
-
二阶导数告诉我们的一阶导数将如何随着输入的变化而改变。
- 它表示只基于梯度信息的梯度下降步骤是否会产生如我们预期的那样大的改善,因此是重要的。
- 我们可以认为,二阶导数是对曲率的衡量。假设我们有一个二次函数(虽然很多实践中的函数都不是二次,但至少在局部可以很好地用二次近似)。
- 如果这样的函数具有零二阶导数,那就没有曲率。也就是一条完全平坦的线,仅用梯度就可以预测它的值。
- 我们使用沿负梯度方向大小为 ϵ \epsilon ϵ的下降步,当该梯度是 1 1 1时,代价函数将下降 ϵ \epsilon ϵ。
- 如果二阶导数是负的,函数曲线向下凹陷 (向上凸出),因此代价函数将下降的比 ϵ \epsilon ϵ多。
- 如果二阶导数是正的,函数曲线是向上凹陷(向下凸出),因此代价函数将下降的比 ϵ \epsilon ϵ少。
- 从图例1可以看出不同形式的曲率如何影响基于梯度的预测值与真实的代价函数值的关系。
-
当我们的函数具有多维输入时,二阶导数也有很多。可以这些导数合并成一个矩阵,称为Hessian矩阵。Hessian矩阵 H ( f ) ( x ) \boldsymbol{H}(f)(\boldsymbol{x}) H(f)(x)定义为:
H ( f ) ( x ) i j = ∂ 2 ∂ x i ∂ x j f ( x ) \boldsymbol{H}(f)(\boldsymbol{x})_{ij}=\displaystyle\frac{\partial^2}{\partial x_i\partial x_j}f(\boldsymbol{x}) H(f)(x)ij=∂xi∂xj∂2f(x) — 公式1 \quad\textbf{---\footnotesize{公式1}} —公式1。
Hessian \text{Hessian} Hessian等价于梯度的 Jacobian \text{Jacobian} Jacobian矩阵。 -
微分算子在任何二阶偏导连续的点处可交换,也就是它们的顺序可以互换: ∂ 2 ∂ x i ∂ x j f ( x ) = ∂ 2 ∂ x j ∂ x i f ( x ) \displaystyle\frac{\partial^2}{\partial x_i\partial x_j}f(\boldsymbol{x})=\displaystyle\frac{\partial^2}{\partial x_j\partial x_i}f(\boldsymbol{x}) ∂xi∂xj∂2f(x)=∂xj∂xi∂2f(x) — 公式2 \quad\textbf{---\footnotesize{公式2}} —公式2
- 这意味着 H i , j = H j , i H_{i,j}=H_{j,i} Hi,j=Hj,i,因此 Hessian \text{Hessian} Hessian矩阵在这些点上是对称的。
- 在深度学习背景下,我们遇到的大多数函数的 Hessian \text{Hessian} Hessian几乎处处都是对称的。
- 因为 Hessian \text{Hessian} Hessian矩阵是实对称的,我们可以将其分解成一组实特征值和特征向量的正交。
- 在特定方向 d \boldsymbol{d} d上的二阶导数可以写成 d ⊤ H d \boldsymbol{d}^\top\boldsymbol{Hd} d⊤Hd。
- 当 d \boldsymbol{d} d是 H \boldsymbol{H} H的一个特征向量时,这个方向的二阶导数就是对应的特征值。
- 对于其他的方向 d \boldsymbol{d} d,方向二阶导数是所有特征值的加权平均,权重在 0 0 0和 1 1 1之间,且与 d \boldsymbol{d} d夹角越小的特征向量有更大的权重。
- 最大特征值确定最大二阶导数,最小特征值确定最小二阶导数。
-
我们可以通过(方向)二阶导数预期一个梯度下降步骤能表现得多好。我们在当前点 x ( 0 ) \boldsymbol{x}^{(0)} x(0)处作函数 f ( x ) f(\boldsymbol{x}) f(x)的近似二阶泰勒级数:
f ( x ) ≈ f ( x ( 0 ) ) + ( x − x ( 0 ) ) ⊤ g + 1 2 ( x − x ( 0 ) ) ⊤ H ( x − x ( 0 ) ) f(\boldsymbol{x})\approx f(\boldsymbol{x}^{(0)})+(\boldsymbol{x}-\boldsymbol{x}^{(0)})^\top\boldsymbol{g}+\displaystyle\frac{1}{2}(\boldsymbol{x}-\boldsymbol{x}^{(0)})^\top\boldsymbol{H}(\boldsymbol{x}-\boldsymbol{x}^{(0)}) f(x)≈f(x(0))+(x−x(0))⊤g+21(x−x(0))⊤H(x−x(0)) — 公式3 \quad\textbf{---\footnotesize{公式3}} —公式3- 其中 g \boldsymbol{g} g是梯度。
- H \boldsymbol{H} H是 x ( 0 ) \boldsymbol{x}^{(0)} x(0)点的 Hessian \text{Hessian} Hessian矩阵。
-
如果我们使用学习速率 ϵ \epsilon ϵ,那么新的点 x \boldsymbol{x} x将会是 x ( 0 ) − ϵ g \boldsymbol{x}^{(0)}-\epsilon\boldsymbol{g} x(0)−ϵg。代入公式3的,我们可以得到:
f ( x ( 0 ) − ϵ g ) ≈ f ( x ( 0 ) ) − ϵ g ⊤ g + 1 2 ϵ 2 g ⊤ H g f(\boldsymbol{x}^{(0)}-\epsilon\boldsymbol{g})\approx f(\boldsymbol{x}^{(0)})-\epsilon\boldsymbol{g}^\top\boldsymbol{g}+\displaystyle\frac{1}{2}\epsilon^2\boldsymbol{g}^\top\boldsymbol{Hg} f(x(0)−ϵg)≈f(x(0))−ϵg⊤g+21ϵ2g⊤Hg — 公式4 \quad\textbf{---\footnotesize{公式4}} —公式4- 其中有 3 3 3项:函数的原始值、函数斜率导致的预期改善、函数曲率导致的校正。
- 当这最后一项太大时, 梯度下降实际上是可能向上移动的。
- 当 g ⊤ H g \boldsymbol{g}^\top\boldsymbol{Hg} g⊤Hg为零或负时,近似的泰勒级数表明增加 ϵ \epsilon ϵ将永远导致 f f f的下降。
- 在实践中,泰勒级数不会在 ϵ \epsilon ϵ大的时候也保持准确,因此在这种情况下我们必须采取更启发式的选择。
- 当 g ⊤ H g \boldsymbol{g}^\top\boldsymbol{Hg} g⊤Hg为正时,通过计算可得,使近似泰勒级数下降最多的最优步长为: ϵ ∗ = g ⊤ g g ⊤ H g \epsilon^\ast=\displaystyle\frac{\boldsymbol{g}^\top\boldsymbol{g}}{\boldsymbol{g}^\top\boldsymbol{Hg}} ϵ∗=g⊤Hgg⊤g — 公式5 \quad\textbf{---\footnotesize{公式5}} —公式5
- 最坏的情况下, g \boldsymbol{g} g与 H \boldsymbol{H} H最大特征值 λ max \lambda_{\text{max}} λmax对应的特征向量对齐,则最优步长是 1 λ max \displaystyle\frac{1}{\lambda_{\text{max}}} λmax1。
- 我们要最小化的函数能用二次函数很好地近似的情况下, Hessian \text{Hessian} Hessian的特征值决定了学习速率的量级。
-
二阶导数测试(second derivative test)
-
二阶导数还可以被用于确定一个临界点是否是局部极大点、局部极小点或鞍点。
- 回想一下,在临界点处 f ′ ( x ) = 0 f'(x)=0 f′(x)=0。
- 而 f ′ ′ ( x ) > 0 f''(x) > 0 f′′(x)>0 意味着 f ′ ( x ) f'(x) f′(x)会随着我们移向右边而增加,移向左边而减小,也就是 f ( x − ϵ ) < 0 f(x-\epsilon)<0 f(x−ϵ)<0和 f ( x + ϵ ) > 0 f(x+\epsilon)>0 f(x+ϵ)>0对足够小的 ϵ \epsilon ϵ成立。
- 换句话说,当我们移向右边,斜率开始指向右边的上坡,当我们移向左边,斜率开始指向左边的上坡。
- 因此我们得出结论,当 f ′ ( x ) = 0 f'(x)=0 f′(x)=0且 f ′ ′ ( x ) > 0 f''(x)>0 f′′(x)>0时, x \boldsymbol{x} x是一个局部极小点。
- 同样,当 f ′ ( x ) = 0 f'(x)=0 f′(x)=0且 f ′ ′ ( x ) < 0 f''(x)<0 f′′(x)<0时, x \boldsymbol{x} x是一个局部极大点。这就是所谓的二阶导数测试(second derivative test)。
- 不幸的是,当 f ′ ′ ( x ) = 0 f''(x)=0 f′′(x)=0时测试是不确定的。在这种情况下, x \boldsymbol{x} x可以是一个鞍点或平坦区域的一部分。
- 在多维情况下,我们需要检测函数的所有二阶导数。
- 利用 Hessian \text{Hessian} Hessian的特征值分解,我们可以将二阶导数测试扩展到多维情况。
- 在临界点处( ∇ x f ( x ) = 0 \nabla_xf(\boldsymbol{x})=0 ∇xf(x)=0),我们通过检测 Hessian \text{Hessian} Hessian的特征值来判断该临界点是一个局部极大点、局部极小点还是鞍点。
- 当
Hessian
\text{Hessian}
Hessian是正定的(所有特征值都是正的),则该临界点是局部极小点。
- 因为方向二阶导数在任意方向都是正的,参考单变量的二阶导数测试就能得出此结论。
- 同样的,当 Hessian \text{Hessian} Hessian是负定的(所有特征值都是负的),这个点就是局部极大点。
- 在多维情况下,实际上可以找到确定该点是否为鞍点的积极迹象(某些情况下)。
- 如果 Hessian \text{Hessian} Hessian的特征值中至少一个是正的且至少一个是负的,那么 x \boldsymbol{x} x是 f f f某个横截面的局部极大点,却是另一个横截面的局部极小点。见图例2中的例子。
- 最后,多维二阶导数测试可能像单变量版本那样是不确定的。
- 当所有非零特征值是同号的且至少有一个特征值是 0 0 0时,这个检测就是不确定的。
- 这是因为单变量的二阶导数测试在零特征值对应的横截面上是不确定的。
- 多维情况下,单个点处每个方向上的二阶导数是不同。
- Hessian \text{Hessian} Hessian的条件数衡量这些二阶导数的变化范围。
- 当 Hessian \text{Hessian} Hessian的条件数很差时,梯度下降法也会表现得很差。
- 这是因为一个方向上的导数增加得很快,而在另一个方向上增加得很慢。
- 梯度下降不知道导数的这种变化,所以它不知道应该优先探索导数长期为负的方向。
- 病态条件数也导致很难选择合适的步长。
- 步长必须足够小,以免冲过最小而向具有较强的正曲率方向上升。
- 这通常意味着步长太小,以致于在其他较小曲率的方向上进展不明显。见图例3的例子。
-
使用 Hessian \text{Hessian} Hessian矩阵的信息指导搜索可以解决这个问题。其中最简单的方法是牛顿法 (Newton’s method)。 牛顿法基于一个二阶泰勒展开来近似 x ( 0 ) \boldsymbol{x}^{(0)} x(0)附近的 f ( x ) f(\boldsymbol{x}) f(x):
f ( x ) ≈ f ( x ( 0 ) ) + ( x − x ( 0 ) ) ⊤ ∇ x f ( x ( 0 ) ) + 1 2 ( x − x ( 0 ) ) ⊤ H ( f ) ( x ( 0 ) ) ( x − x ( 0 ) ) f(\boldsymbol{x})\approx f(\boldsymbol{x}^{(0)})+(\boldsymbol{x}-\boldsymbol{x}^{(0)})^\top\nabla_xf(\boldsymbol{x}^{(0)})+\frac{1}{2}(\boldsymbol{x}-\boldsymbol{x}^{(0)})^\top\boldsymbol{H}(f)(\boldsymbol{x}^{(0)})(\boldsymbol{x}-\boldsymbol{x}^{(0)}) f(x)≈f(x(0))+(x−x(0))⊤∇xf(x(0))+21(x−x(0))⊤H(f)(x(0))(x−x(0)) — 公式6 \quad\textbf{---\footnotesize{公式6}} —公式6 -
接着通过计算,我们可以得到这个函数的临界点: x ∗ = x ( 0 ) − H ( f ) ( x ( 0 ) ) − 1 ∇ x f ( x ( 0 ) ) \boldsymbol{x}^\ast=\boldsymbol{x}^{(0)}-\boldsymbol{H}(f)(\boldsymbol{x}^{(0)})^{-1}\nabla_xf(\boldsymbol{x}^{(0)}) x∗=x(0)−H(f)(x(0))−1∇xf(x(0)) — 公式7 \quad\textbf{---\footnotesize{公式7}} —公式7
-
仅使用梯度信息的优化算法被称为一阶优化算法(first-order optimization algorithms),如梯度下降。
-
使用 Hessian \text{Hessian} Hessian矩阵的优化算法被称为二阶最优化算法(secondorder optimization algorithms)(Nocedal and Wright, 2006),如牛顿法。
-
在深度学习中大多数上下文中使用的优化算法适用于各种各样的函数,但几乎都没有保证。
- 因为在深度学习中使用的函数族是相当复杂的,所以深度学习算法往往缺乏保证。
- 在许多其他领域,优化的主要方法是为有限的函数族设计优化算法。
-
在深度学习的背景下,限制函数满足Lipschitz连续(Lipschitz continuous)或其导数 Lipschitz \text{Lipschitz} Lipschitz连续可以获得一些保证。
-
Lipschitz
\text{Lipschitz}
Lipschitz连续函数的变化速度以Lipschitz常数(Lipschitz constant)
L
\mathcal{L}
L为界:
∀ x , ∀ y , ∣ f ( x ) − f ( y ) ∣ ≤ L ∥ x − y ∥ 2 \forall\boldsymbol{x},\forall\boldsymbol{y},|f(\boldsymbol{x})-f(\boldsymbol{y})|\leq\mathcal{L}\Vert\boldsymbol{x}-\boldsymbol{y}\Vert_2 ∀x,∀y,∣f(x)−f(y)∣≤L∥x−y∥2 — 公式8 \quad\textbf{---\footnotesize{公式8}} —公式8 - 这个属性允许我们量化我们的假设—梯度下降等算法导致的输入的微小变化将使输出只产生微小变化,因此是很有用的。
- Lipschitz \text{Lipschitz} Lipschitz连续性也是相当弱的约束,并且深度学习中很多优化问题经过相对较小的修改后就能变得 Lipschitz \text{Lipschitz} Lipschitz连续。
-
Lipschitz
\text{Lipschitz}
Lipschitz连续函数的变化速度以Lipschitz常数(Lipschitz constant)
L
\mathcal{L}
L为界:
-
最成功的特定优化领域或许是凸优化(Convex optimization)。
- 凸优化通过更强的限制提供更多的保证。
- 凸优化算法只对凸函数适用——即 Hessian \text{Hessian} Hessian处处半正定的函数。
- 因为这些函数没有鞍点而且其所有局部极小点必然是全局最小点,所以表现很好。
- 然而,深度学习中的大多数问题都难以表示成凸优化的形式。
- 凸优化仅用作的一些深度学习算法的子程序。
- 凸优化中的分析思路对证明深度学习算法的收敛性非常有用,然而一般来说,深度学习背景下的凸优化的重要性大大减少。
- 有关凸优化的详细信息,见Boyd and Vandenberghe (2004) 或Rockafellar (1997)。
-
-
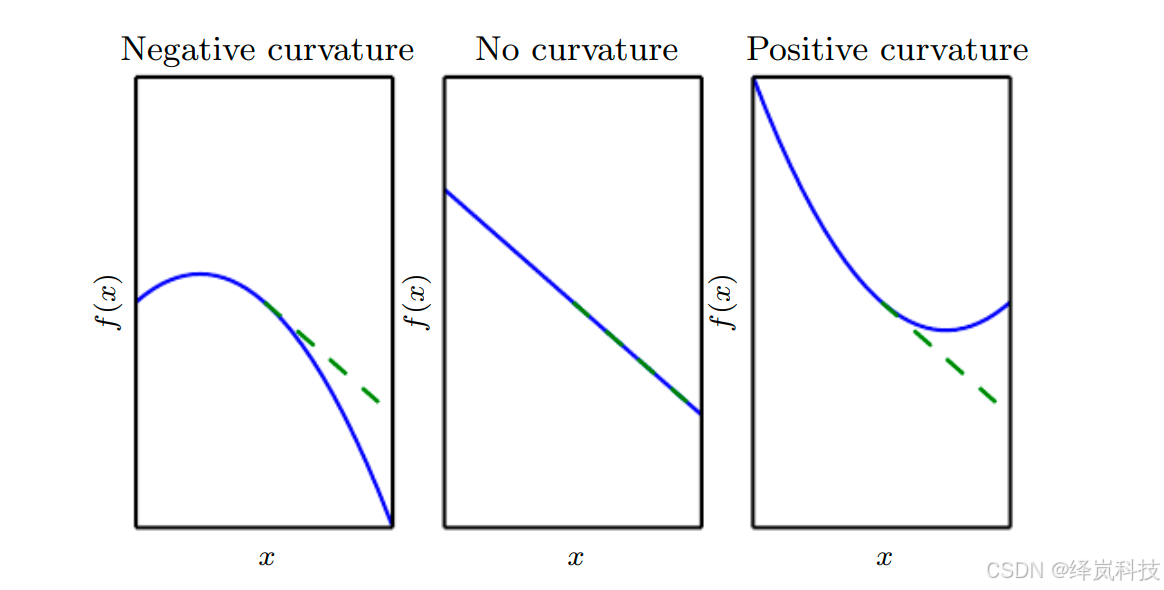
二阶导数确定函数的曲率。
-
说明:
- 这里我们展示具有各种曲率的二次函数。
- 虚线表示我们仅根据梯度信息进行梯度下降后预期的代价函数值。
- 对于负曲率,代价函数实际上比梯度预测下降得更快。
- 没有曲率时,梯度正确预测下降值。
- 对于正曲率,函数比预期下降得更慢,并且最终会开始增加,因此太大的步骤实际上可能会无意地增加函数值。
-
-
-
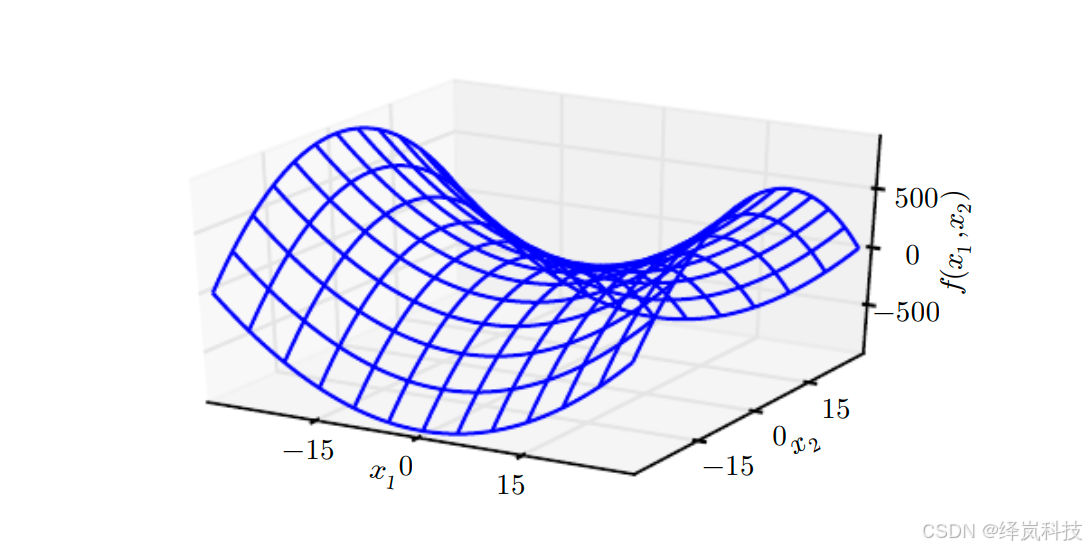
既有正曲率又有负曲率的鞍点。
-
说明:
- 示例中的函数是 f ( x ) = x 1 2 − x 2 2 f(\boldsymbol{x})=x_1^2-x_2^2 f(x)=x12−x22。
- 函数沿 x 1 x_1 x1轴向上弯曲。 x 1 x_1 x1轴是 Hessian \text{Hessian} Hessian的一个特征向量,并且具有正特征值。
- 函数沿 x 2 x_2 x2轴向下弯曲。该方向对应于 Hessian \text{Hessian} Hessian负特征值的特征向量。
- 名称“鞍点“源自该处函数的鞍状形状。这是具有鞍点函数的典型示例。
- 维度多于一个时,鞍点不一定要具有 0 0 0特征值:仅需要同时具有正特征值和负特征值。
- 我们可以想象这样一个鞍点(具有正负特征值)在一个横截面内是局部极大点,另一个横截面内是局部极小点。
-
-
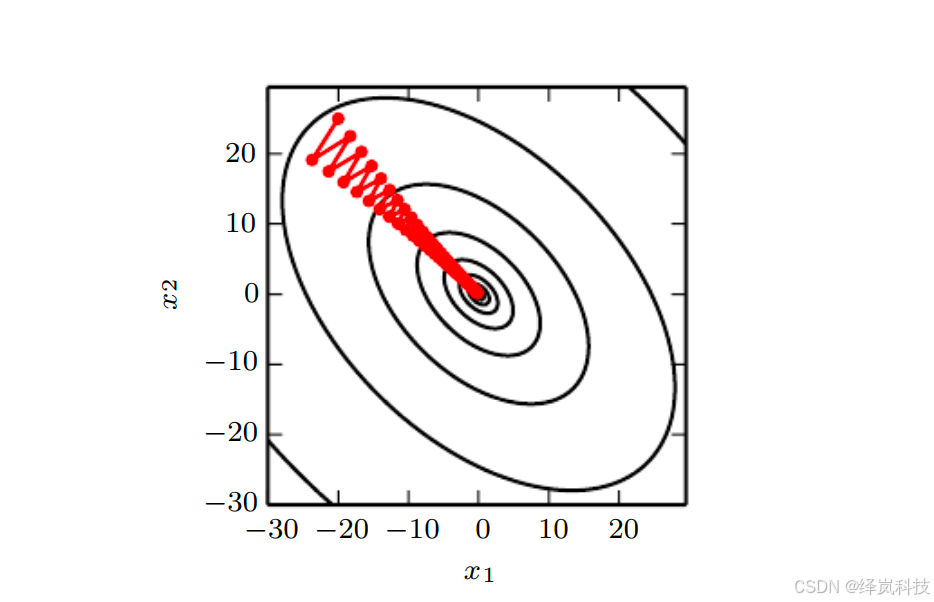
图例3:梯度下降无法利用包含在 Hessian \text{Hessian} Hessian矩阵中的曲率信息。
-
梯度下降无法利用包含在 Hessian \text{Hessian} Hessian矩阵中的曲率信息。
-
说明:
- 梯度下降无法利用包含在 Hessian \text{Hessian} Hessian矩阵中的曲率信息。
- 这里我们使用梯度下降来最小化 Hessian \text{Hessian} Hessian矩阵条件数为 5 5 5的二次函数 f ( x ) f(\boldsymbol{x}) f(x)。
- 这意味着最大曲率方向具有比最小曲率方向多五倍的曲率。
- 在这种情况下,最大曲率在 [ 1 , 1 ] ⊤ [1,1]^\top [1,1]⊤方向上,最小曲率在 [ 1 , 1 ] ⊤ [1,1]^\top [1,1]⊤方向上。
- 红线表示梯度下降的路径。这个非常细长的二次函数类似一个长峡谷。
- 梯度下降把时间浪费于在峡谷壁反复下降,因为它们是最陡峭的特征。
- 由于步长有点大,有超过函数底部的趋势,因此需要在下一次迭代时在对面的峡谷壁下降。
- 与指向该方向的特征向量对应的 Hessian \text{Hessian} Hessian的大的正特征值表示该方向上的导数快速增加,因此基于 Hessian \text{Hessian} Hessian的优化算法可以预测,在此情况下最陡峭方向实际上不是有前途的搜索方向。
-
总结
Jacobian \text{Jacobian} Jacobian矩阵与 Hessian \text{Hessian} Hessian矩阵作为梯度概念的延伸与深化,为我们在处理复杂多变量函数时提供了更为精细的工具。它们不仅拓宽了我们对函数性质的理解,更为设计高效、稳定的数值计算方法与优化算法奠定了坚实基础。在机器学习、科学计算等众多领域,这些矩阵的应用正日益广泛,成为推动技术进步的关键力量。