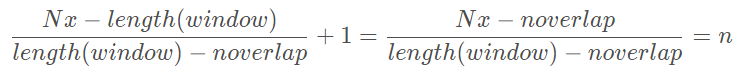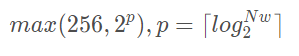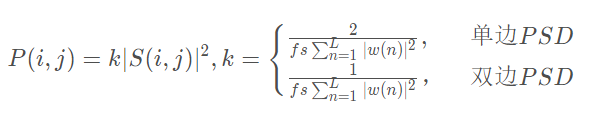目录
2.短时傅里叶变换(Short-time Fourier Transform,STFT)
信号处理基础——傅里叶变换与短时傅里叶变换
1.FT与STFT概述
对于大多数信号而言, 傅立叶分析绝对是非常有用的,因为频率分析在大多数情况下都非常重要。 那么为什么我们还需要研究短时傅里叶变换呢(STFT)?
原因是因为傅立叶分析有一个非常严重的缺点, 在将信号从时间域变换到频率域去的时候,把时间信息丢失了。 当我们在用傅立叶变化去分析一个具体信号的时候, 我们不知道哪个频率是对应在哪个时间点出现的,在哪个时间点消失的。
如果一个信号的频率并不随着时间变化, 那么我们称它为平稳信号。 那么知道哪一个频率的信号在哪一个时间点出现的就不那么重要了。 可是如果现实生活中我们研究的大多数信号都是非平稳信号,他们都许多非常短暂变化的特性, 这些特点对于我们信号分析的特点, 傅立叶分析并不适合去做这种分析,而短时傅里叶变换则可以。
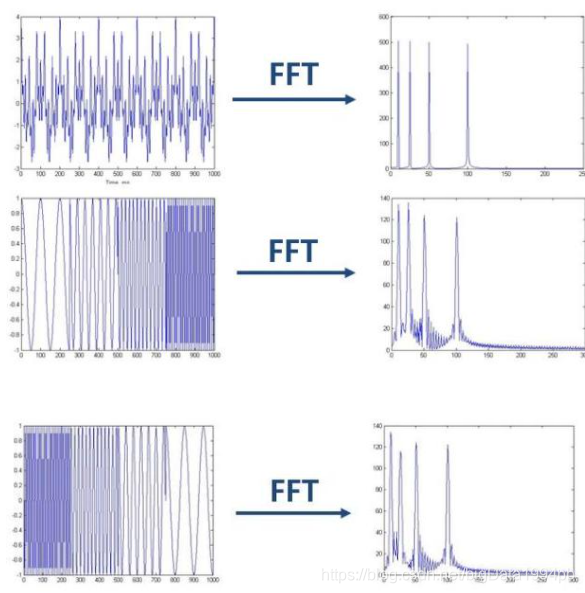
如上图所示,最上边的是频率始终不变的平稳信号。而下边两个则是频率随着时间改变的非平稳信号,它们同样包含和最上信号相同频率的四个成分。做FFT后,我们发现这三个时域上有巨大差异的信号,频谱(幅值谱)却非常一致。尤其是下边两个非平稳信号,我们从频谱上无法区分它们,因为它们包含的四个频率的信号的成分确实是一样的,只是出现的先后顺序不同。
可见,傅里叶变换处理非平稳信号有天生缺陷。它只能获取一段信号总体上包含哪些频率的成分,但是对各成分出现的时刻并无所知。因此时域相差很大的两个信号,可能频谱图一样。
然而平稳信号大多是人为制造出来的,自然界的大量信号几乎都是非平稳的,所以在比如生物医学信号分析等领域的论文中,基本看不到单纯傅里叶变换这样naive的方法。
2.短时傅里叶变换(Short-time Fourier Transform,STFT)
一个简单可行的方法就是——加窗。 “把整个时域过程分解成无数个等长的小过程,每个小过程近似平稳,再傅里叶变换,就知道在哪个时间点上出现了什么频率了。”这就是短时傅里叶变换。
3.spectrogram函数
[S,F,T,P]=spectrogram(x,window,noverlap,nfft,fs) %有返回值
spectrogram(x,window,noverlap,nfft,fs,'yaxis') %无返回值调用,直接输出频谱图
matlab中的spectrogram函数来做短时傅里叶变换,下面是其参数的解释。
语法:
[S,F,T,P]=spectrogram(x,window,noverlap,nfft,fs)
[S,F,T,P]=spectrogram(x,window,noverlap,F,fs)
说明:当使用时无输出参数,会自动绘制频谱图;有输出参数,则会返回输入信号的短时傅里叶变换。当然也可以从函数的返回值S,F,T,P绘制频谱图,具体参见例子。
参数:
x---输入信号的向量。默认情况下,即没有后续输入参数,x将被分成8段分别做变换处理,
如果x不能被平分成8段,则会做截断处理。默认情况下,其他参数的默认值为
window---窗函数,默认为nfft长度的海明窗Hamming
noverlap---每一段的重叠样本数,默认值是在各段之间产生50%的重叠
nfft---做FFT变换的长度,默认为256和大于每段长度的最小2次幂之间的最大值。
fs---采样频率,默认值归一化频率 .
Window---窗函数,如果window为一个整数,x将被分成window段,每段使用Hamming窗函数加窗。
如果window是一个向量,x将被分成length(window)段,每一段使用window向量指定的
窗函数加窗。所以如果想获取specgram函数的功能,只需指定一个256长度的Hann窗.
4.注意事项
nfft越大,频域的分辨率就越高(分辨率=fs/nfft),但离瞬时频率就越远;
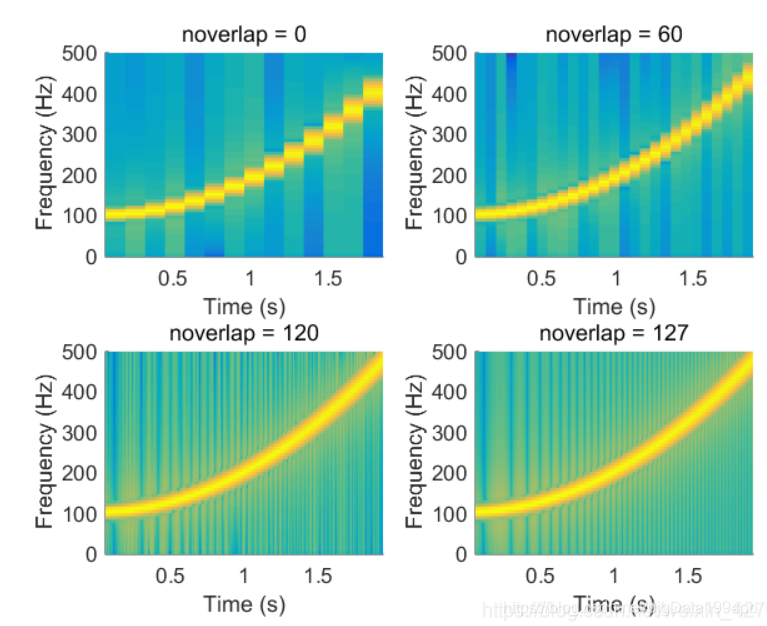
noverlap影响时间轴的分辨率,越接近nfft,分辨率越高,相应的冗余就越多,计算量越大,但计算机只要能承受,问题不大。
[S,F,T,P]=spectrogram(x,window,noverlap,nfft,fs) %有返回值
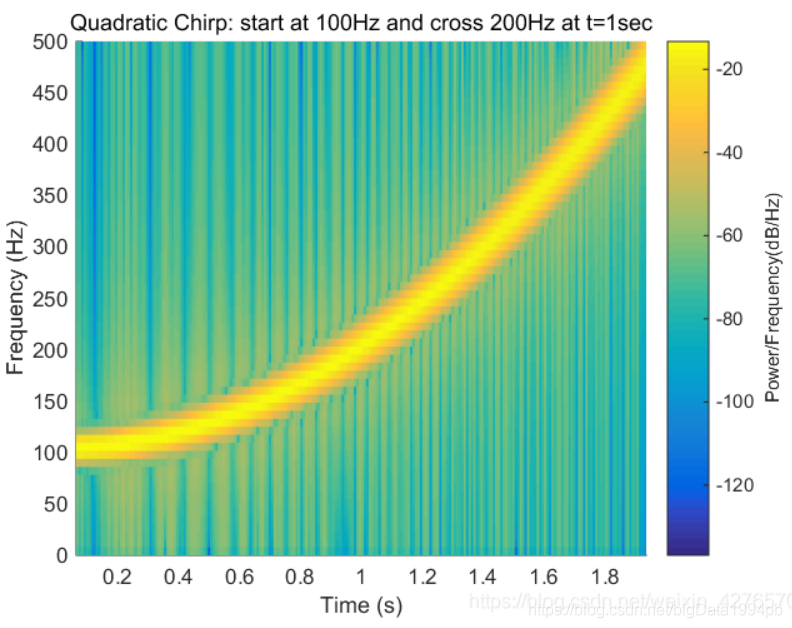
spectrogram(x,window,noverlap,nfft,fs,'yaxis') %无返回值调用,直接输出频谱图需要注意的是,上述调用方式中,若输入参数为缺省值,则会以默认参数(见Note中推荐文档)进行计算。以MATLAB自带的非平稳信号quadratic chirp为例,对其进行时频分析,测试代码如下:
Nw = 128; %窗函数长度 window = hamming(128); % 使用海明窗(默认窗函数) noverlap = 120; %重叠长度 nfft = 2^nextpow2(length(window)); %DFT点数 fs = 1000; %采样率 t=0:1/fs:2; % 2 secs @ 1kHz sample rate y=chirp(t,100,1,200,'q'); % Start @ 100Hz, cross 200Hz at t=1sec spectrogram(y, window, noverlap, nfft,fs, 'yaxis'); % Display the spectrogram h=colorbar; h.Label.String = 'Power/Frequency(dB/Hz)' title('Quadratic Chirp: start at 100Hz and cross 200Hz at t=1sec');
1. 如何分析这个图?
颜色:首先最重要的一点是,该图像不同颜色区域表示的是对应频率下信号功率谱密度的分贝值,即单位为Power/Frequency(dB/Hz);
时间轴: 其次,时间轴表示的是信号时长,其长度n为
该数值表示在这信号时长内进行了多少次快速傅里叶变换,该数值由窗函数的宽度和重叠区域长度共同决定;
频率轴:频率轴以模拟频率表示,其显示范围为采样频率的一半。 为什么呢?由傅里叶变换和采样定理知识我们可以知道,信号经过傅里叶变换后频谱对称,实际信号频率范围其实只有采样频率一半。由于频率轴只显示采样频率一半,故其长度为nfft/2+1或(nfft+1)/2,分别对应nfft为even和odd。频率轴的分辨率受nfft的影响,为1/nfft*fs。
2. DFT点数nfft的选择
这个值的选择与快速傅里叶变换中一致,通常取最接近信号长度的2的整数次幂,即 nfft = 2^nextpow2(length(window)) ,这里的信号长度即窗函数长度,因为是对每个加窗信号的快速傅里叶变换。缺省值为3. noverlap对输出结果的影响
noverlap表示窗函数在移动过程中与前一个窗口位置的重叠区域大小,从前面对时间轴的分析公式可以看到,该参数会影响时间轴的分辨率。当该参数为0时,信号被窗函数进行无间隔无重叠分配,可以想象执行该过程时,时间轴上每一个数据长度(Nw)对应一个持续的fft显示,图像上表现为时间轴上出现明显的“拉伸”。而随着noverlap参数的引入,增大了时间轴分辨率,即每隔(Nw - noverlap)长度进行一次频率轴的更新,随着noverlap逐渐接近Nw,图像上表现为时间轴更加“细腻”,但随之而来的肯定是计算次数的增加。窗口长度Nw对输出结果的影响
窗口长度对短时傅里叶变换的影响不言而喻,窗口大则频域分辨率越高,相应的时间上分辨率下降。该值的正确选择是短时傅里叶算法的一个难题,故引出了小波变换等方法。如何由带返回值的调用形式得到一致的频谱图呢?
[S,F,T,P]=spectrogram(x,window,noverlap,nfft,fs)
1. 参数S和P的关系
S为信号x进行n次快速傅里叶变换后的结果,为一复数矩阵,横向按时间递增,纵向按频率递增。包含nfft/2+1或(nfft+1)/2行、n列,推导见前述。P为信号的功率谱密度,为一实矩阵,维数与S保持一致。
由信号分析的知识可以知道,功率谱密度可以由信号的快速傅里叶变换结果的绝对值平方除以信号长度表示,但是在这里,为了弥补窗函数的影响,还需要添加一个变换系数k。即当函数spectrogram()直接调用时输出的是以分贝值表示的PSD,由上面的讨论,我们可以利用S或者P得到一致的谱图
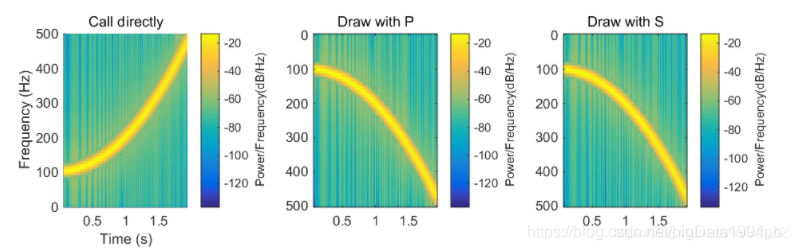
clear Nw = 128; window = hamming(128); noverlap = 120; nfft = 2^nextpow2(length(window)); fs = 1000; t=0:1/fs:2; % 2 secs @ 1kHz sample rate y=chirp(t,100,1,200,'q'); % Start @ 100Hz, cross 200Hz at t=1sec subplot(131) spectrogram(y, window, noverlap, nfft,fs, 'yaxis'); % Display the spectrogram title('Call directly') h=colorbar; h.Label.String = 'Power/Frequency(dB/Hz)' [S, F, T, P] = spectrogram(y, window, noverlap, nfft,fs); subplot(132) imagesc(T,F,10*log10(P)); title('Draw with P') h=colorbar; h.Label.String = 'Power/Frequency(dB/Hz)' subplot(133) k = 2/(fs*(window'*window)) imagesc(T,F,10*log10(abs(S).*abs(S)*k)); title('Draw with S') h=colorbar; h.Label.String = 'Power/Frequency(dB/Hz)'
2.关于参数T的认识
我们已经知道输出的图像时间轴分辨率受制于窗口大小Nw和重叠长度noverlap,其长度为k。T中的数值为每个segment的中间值,什么意思呢?这里的segment理解为加的窗口,以本文中的程序为例,我使用的是采样频率为1000Hz的2s chirp信号,窗口长度Nw为128,noverlap为120。那么T的第一个数据该是多少?即1/1000 * 128/2 = 0.064s,而后每次递增1/1000 *(Nw - noverlap)= 0.008s。
了解了T的含义后,我们便可以根据结果(S、P)分别得到各个时间segment的频谱,例如我想查看信号1秒附近(±Nw/1000/2 s)的功率谱,只需要输入plot(P(:, find(T==1)))。
f = 100:0.05:300; [S, F, T, P] = spectrogram(y, window, noverlap, f,fs); spectrogram(y, window, noverlap, f,fs, 'yaxis'); % [S,F,T] = SPECTROGRAM(X,WINDOW,NOVERLAP,F,Fs) where F is a vector of % frequencies in Hz (with 2 or more elements) computes the spectrogram at % those frequencies using the Goertzel algorithm. The specified % frequencies in F are rounded to the nearest DFT bin commensurate with % the signal's resolution.该调用方式下,nfft由具体的频率范围取代,频率轴显示范围由f上下限决定,频率分辨率由其间隔决定。
5.实例分析
例.计算并显示二次扫频信号的PSD图,扫频信号的频率开始于100Hz,在1s时经过200Hz
T = 0:0.001:2;
X = chirp(T,100,1,200,'q');
spectrogram(X,128,120,128,1E3);
title('Quadratic Chirp');例.计算并显示线性扫频信号的PSD图,扫频信号由直流开始,在1s时经过150Hz,控制频率轴显示在y轴上
T = 0:0.001:2;
X = chirp(T,0,1,150);
[S,F,T,P] = spectrogram(X,256,250,256,1E3);
surf(T,F,10*log10(P),'edgecolor','none'); axis tight;
view(0,90);
xlabel('Time (Seconds)'); ylabel('Hz');6.Chirp信号及其生成
(1)简介
Chirp译名:啁啾(读音:“周纠”),是通信技术有关编码脉冲技术中的一种术语,是指对脉冲进行编码时,其载频在脉冲持续时间内线性地增加,当将脉冲变到音频地,会发出一种声音,听起来像鸟叫的啁啾声,故名“啁啾”。
后来就将脉冲传输时中心波长发生偏移的现象叫做“啁啾”。例如在光纤通信中由于激光二极管本身不稳定而使传输单个脉冲时中心波长瞬时偏移的现象,也叫“啁啾”。
Chirp信号的表达式如下:
-
式中f0称作起始频率。
-
u0为调频率
-
对相位进行求导,得到角频率以及频率随时间的线性变化关系 f = f0+u0*t
(2)matlab生成chirp信号
t=0: 1/44100 :0.05; % 采样率是44100HZ
y=chirp(t, 3000, 0.05, 8000); % 第一个参数表示时间长度,第二个参数表示当t=0s时对应的频率,第三个和第四个参数为当t=0.05s时对应的频率
subplot(2,1,1);
plot(y);
subplot(2,1,2);
spectrogram(y,256,250,256,44100); (3)chirp函数
y = chirp(t,f0,t1,f1,’method’,phi,'shape')
根据指定的方法在时间t上产生余弦扫频信号,f0为第一时刻的瞬时频率,f1为t1时刻的瞬时频率,f0和f1单位都为Hz。如果未指定,f0默认为e-6(对数扫频方法)或0(其他扫频方法),t1为1,f1为100Hz。
扫频方法有linear线性扫频、quadratic二次扫频、logarithmic对数扫频;
phi允许指定一个初始相位(以°为单位),默认为0,如果想忽略此参数,直接设置后面的参数,可以指定为0或[];
shape指定二次扫频方法的抛物线的形状,凹还是凸,值为concave或convex,如果此信号被忽略,则根据f0和f1的相对大小决定是凹还是凸。
(4)例子
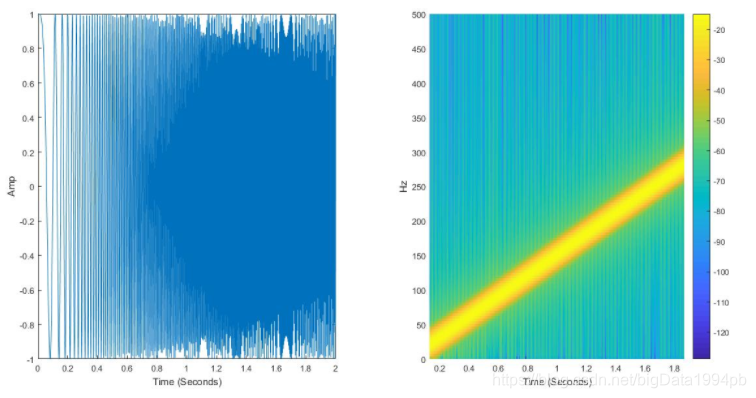
使用短时傅里叶变换对线性扫描频率信号进行谱估计的命令如下:
clear all;clc;close all; %clear all清空工作区,clc清空命令(可能是clear command缩写),close all关闭所有窗口
T=0:0.001:2;
X=chirp(T,0,1,150);
subplot(121);plot(T,X);
xlabel('Time (Seconds)');ylabel('Amp');
subplot(122);[S,F,T,P]=spectrogram(X,256,250,256,1E3);
surf(T,F,10*log10(P),'edgecolor','none');axis tight;
xlabel('Time (Seconds)');ylabel('Hz');
view(0,90);
colorbar;7.时频分析实战代码
%时频分析
clc;
data=load('dataset/opendataset/dataset.mat');
Au=data.x_train(:,1,3);
Fs = 256;
%短时傅里叶
[B, F, T, P] = spectrogram(Au,256,255,500,Fs); % B是F大小行T大小列的频率峰值,P是对应的能量谱密度
figure
imagesc(T,F,abs(B));
set(gca,'YDir','normal')
ylim([0,35]);
colorbar;
xlabel('时间 t/s');
ylabel('频率 f/Hz');
title('短时傅里叶时频图');
% 小波
wavename='cmor3-3';
totalscal=300;
Fc=centfrq(wavename); % 小波的中心频率
c=2*Fc*totalscal;
scals=c./(1:totalscal);
f=scal2frq(scals,wavename,1/Fs); % 尺度转换为频率
coefs=cwt(Au,scals,wavename); % 连续小波系数
t=0:1/Fs:4.5-1/Fs;
figure
imagesc(t,f,abs(coefs));
set(gca,'YDir','normal')
ylim([0,35]);
colorbar;
xlabel('时间 t/s');
ylabel('频率 f/Hz');
title('小波时频图');
%新版cwt
figure
cwt(Au,Fs);
8. 案例分析
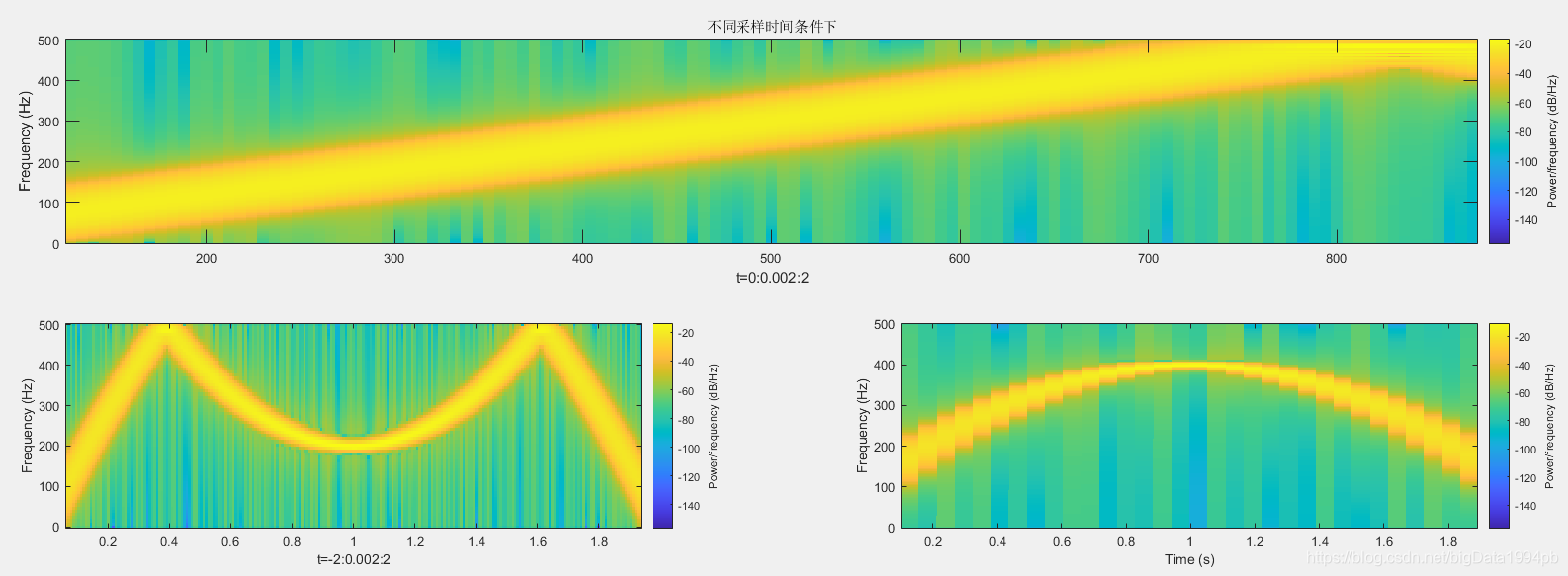
计算谱图与现行调频信号瞬时频率偏差
clear all;
t = 0:0.002:2;
y1 = chirp(t,0,1,150);
subplot(311);
%spectrogram(y,window,noverlop,nfft,fn,'yaxis')无返回值,直接输出时频图
%[S,F,T,P] = spectrogram(y,window,noverlop,nfft,fn)有返回值
spectrogram(y1,256,250,256,1E3,'yaxis');
xlabel('t=0:0.002:2');
title('不同采样时间条件下');
% 产生余弦扫频信号
t = -2:0.002:2;
y2 = chirp(t,100,1,200,'quadratic');
subplot(323);
spectrogram(y2, 128,120,128,1E3,'yaxis');
xlabel('t=-2:0.002:2');
t = -1:0.001:1;
% []表示忽略初始相位的设置也可以设置0或者自己设置
% 指定扫频方法的抛物线的凹凸性,为concave或者convex
y3 = chirp(t,100,1,400,'q',[],'convex');
subplot(324);
spectrogram(y3, 256, 200, 256, 1000, 'yaxis');结果如下:
参考文献
[1]https://ddong7.blog.csdn.net/article/details/108695223
[2]https://blog.csdn.net/weixin_30547797/article/details/99118894