二分法是一种查找效率较高的方法,在编程中十分常见。话不多说,现在,我们来学习一下二分吧 •ࡇ•
1什么是二分
1.1二分查找(Binary Search)
1.1.1基础认知
顾名思义,“二分”就是将数组劈成两半,每一次总是查找中间的数。也叫折半搜索。数字炸弹的游戏大家应该都玩过,如果按顺序猜数,效率肯定没有从中间猜那么高。
下面是二分查找的核心步骤。
①初始状态:数组的首尾各有一个标记,分别记为left和right
(根据不同习惯也可使用low和high)。
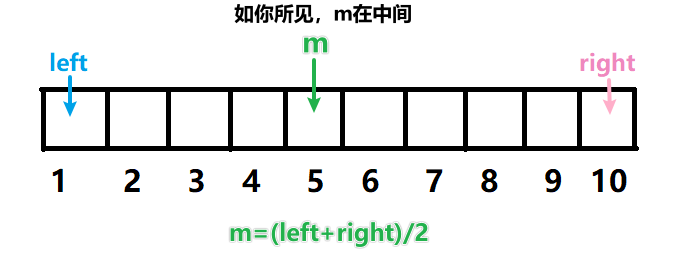
②循环条件:while(left<right)。因为left和right在二分未找到key的过程中总是相互靠近,直至指向同一个位置。所以left==right时循环才停止。
③判断条件:以升序数组的二分查找为例,将a[m]与要查找的数key作比较。
如果a[m]小于key,说明key在a[m]右侧,则将数组从左向右压缩一半,把left用力向右推,推到m的右边,也就是第6位,相当于把左边的数据都屏蔽了,因为key不可能在左半边。
同理,如果a[m]大于key,说明key在a[m]左侧,则将数组从右向左压缩一半,把right用力向左推,推到m的左边,也就是第4位,key不可能在右半边。
本例中,假设key=36,

二分查找有一个大前提:数组必须有序。
很显然,如果数组乱序,那么比较后标记left和right的移动就是混乱的。
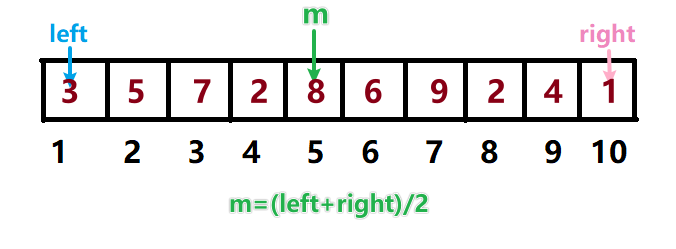
比如在下图这个乱序的数组中查找位于第9位的"4",那么第一次查找后right就会移动到m前面第4位的位置上,下一次就只能在下标1~4的序列中查找,就不可能查找到第9位的正确位置。这样的话,二分查找就没有意义。
1.1.2核心代码
下面是用C++语言描述的最简单的二分查找代码:
int binary_search(int start, int end, int key) {
int ret = -1; // 未搜索到数据返回-1下标
int mid;
while (start <= end) {
//mid = (end - start)/2; 直接平均的一般写法
mid = start + ((end - start) >> 1); // 直接平均可能会溢出,所以用这个算法
if (arr[mid] < key)
start = mid + 1;
else if (arr[mid] > key)
end = mid - 1;
else { // 最后检测相等是因为多数搜索情况不是大于就是小于
ret = mid;
break;
}
}
return ret; // 单一出口
}第5,6行注释:对于n是有符号数的情况,当你可以保证 n>=0时,n >> 1 比 n / 2 指令数更少。
以上就是二分查找的基础内容。
1.2二分答案
解题的时候往往会考虑枚举答案然后检验枚举的值是否正确。若满足单调性,则满足使用二分法的条件。把这里的枚举换成二分,就变成了 「二分答案」。
这里以一个经典的二分答案题目为例(来自洛谷-二分题单)P1873 [COCI 2011/2012 #5] EKO / 砍树
题目理解上并不困难,就是在可能解的范围[0, max]内进行二分,每次假定H = (l + r + 1) / 2为答案,然后根据这个假设的答案H,结合贪心法来验证能否得到相应多的木材。
Q:那么,为什么是H = (l + r + 1) / 2而不是H = (l + r ) / 2呢?
这里其实并不能单独把这个语句拎出来考虑,而要结合下面l和r的移动方式(要不要+1/-1)。这就是二分的偏向和区间移动有机结合的灵活性所在,也是题目能否正确运行出结果的关键。
1. 如果上面H =(l + r) / 2, H偏向l,则l不能等于H,必须为l=H+1,因为可能会出现 l一直小于r的情况,导致死循环。
2. 但改成H = (l + r + 1) / 2, 使H偏向r,则可以使l=H,因为当处于l=r-1的位置时,H偏向r,则l能够跟随H偏向右移动,可以走到最后l=r使循环结束。
以下是AC代码,可以手动模拟一下不同写法下,走到l和r相邻时的情况,能更直观地感受和理解上述的灵活性。(动手动脑噢!ᕙ(`▿´)ᕗ)
using namespace std;
#include <iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
long long n, m;//树木数量n,需要木材m
long long a[1000005];
int main()
{
int i;
long long max = 0; //注意数据范围,int是不够的,会溢出
long long l, r;
long long sum, top, H;
scanf("%lld%lld", &n, &m);
for (i = 1; i <= n; i++) {
scanf("%lld",&a[i]);
if (a[i] > max)max = a[i]; //记录最高的树高为max
}
l = 0; r = max;
while (l < r) {
H = (l + r + 1) / 2;
sum = 0;
for (i = 1; i <= n; i++) {
//每棵树被砍掉的部分长度相加
top = ((a[i] - H) >= 0) ? (a[i] - H) : 0;
sum += top;
}
if (sum < m)r = H - 1;
else if (sum == m) {
printf("%lld", H);
break;
}
else l = H; //如果上面H =(l + r) / 2,则l不能等于H,必须l=H+1,因为可能会出现l一直小于r
//但改成H = (l + r + 1) / 2,使H偏向r,则可以使l=H,因为当处于l=r-1的位置时,H偏向r,则l向右移动可以有l=r使循环结束。
}
if (l == r) printf("%lld", l);
return 0;
}(以下两问答摘录自OI Wiki)
为何搜索区间是左闭右开的?
因为搜到最后,会这样(以合法的最大值为例):
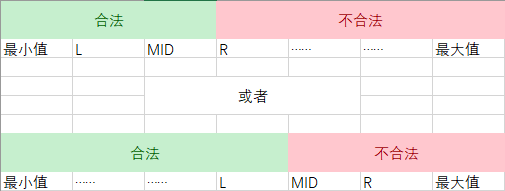
然后会
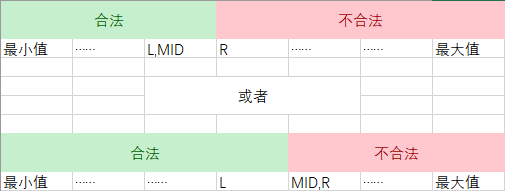
合法的最小值恰恰相反。
为何返回左边值?
同上。L总是最优解
1.3最大值最小化/最小值最大化
这一类题目中我们要求一个二分区间序列,左侧或右侧中的一侧满足某种条件,但另一侧都不满足某种条件。
注意,这里的有序是广义的有序,如果一个数组中的左侧或者右侧都满足某一种条件,而另一侧都不满足这种条件,也可以看作是一种有序(如果把满足条件看做0,不满足看做1,至少对于这个条件的这一维度是有序的)。换言之,二分搜索法可以用来查找满足某种条件的最大(最小)的值。
要求满足某种条件的最大值的最小可能情况(最大值最小化),首先的想法是从小到大枚举这个作为答案的「最大值」,然后去判断是否合法。若答案单调,就可以使用二分搜索法来更快地找到答案。因此,要想使用二分搜索法来解这种「最大值最小化」的题目,需要满足以下三个条件:
答案在一个固定区间内;
可能查找一个符合条件的值不是很容易,但是要求能比较容易地判断某个值是否是符合条件的;
可行解对于区间满足一定的单调性。换言之,如果x是符合条件的,那么有x-1或者x+1也符合条件。(这样下来就满足了上面提到的单调性)
例题
这里有一道题要求我们查找满足条件的最小值的最大值,来自洛谷二分题单的P2678。
一开始写的时候,由于是第一次接触这类最小值最大化的题目,所以误入了歧途,被移动的最大石头数量限制住了思维,试图从提前计算出间隔大小来入手,并且将移动石头的个数严格限制在了M以内,所以思路就变得很乱,很难下手,效率也不高。
后来参考了这一篇题解:题解 P2678 【跳石头】 - ShawnZhou 的博客 - 洛谷博客 (luogu.com.cn)
(写得很好,通俗易懂,很详细)
总结出这一类题的核心:
在可行解的范围[l, r]内进行二分,二分的判断依靠judge函数
保留满足条件的可行解暂时存储为答案ans,然后接着向更可能有可行最优解的方向(条件更苛刻)继续二分。
如果二分到的答案是非法解,就往更可能有可行解的方向(条件更宽松)继续二分。
judge函数的设计根据题意而异,但大体上的思想都是——想办法检测这个解是不是合法。
本题中,我们去判断如果以这个距离为最短跳跃距离需要移走多少块石头,先不必考虑限制移走多少块,等全部拿完再把拿走的数量和限制进行比对,如果超出限制,那么这就是一个非法解,反之就是一个合法解。
main函数的二分部分中,要注意 二分的结束条件(l<=r)和 l,r的移动(l=m+1和r=m-1),这两部分的设计需要考虑极端情况下的处理,例如l和r相邻时或者l==r时,m的左右偏向会不会导致死循环等。最简单的处理办法就是模拟这样的情况,仔细思考哪种写法能够满足题目要求且不会导致死循环。需要自己去思考。
AC代码如下,建议读完题解后配合注释食用。同样请读者们思考偏向和区间移动的关系。◕‿◕
using namespace std;
#include <iostream>
int L, N, M; //L总距离,N岩石数,M至多移走的岩石数
int d[50005]; //每块岩石与起点的距离,升序
/*judge函数,用于判断解是否合法*/
bool judge(int m) { //m:二分出后假定的答案
int move = 0; //move:计数器,记录移走的岩石数
int now = 0; //**now:表示模拟跳石头的人当前所在位置**
for (int i = 1; i <= N + 1; i++) { //i表示下一块石头的编号
//**N不是终点,N+1才是!**
//遍历,模拟跳一趟
if (d[i] - d[now] < m) move++;//如果本次跳跃的间隔小于假设的的结果m
//则移走,不用跳,然后考虑下一块石头。
else now = i; //如果这块石头不用拿走,则跳到下一块石头。
}
if (move > M)return false; //移走的石头个数大于规定值时返回false
else return true; //反之则m是可行解,返回true
}
/*main函数,主要是二分的过程*/
int main()
{
int l, r, m;
int ans = 0; //ans最终输出的结果
cin >> L >> N >> M;
for (int i = 1; i <= N; i++) {
cin >> d[i];
}
d[N + 1] = L;
l = 1;
r = L;
while (l <= r) {
m = (r + l) / 2;
if (judge(m)) {
//如果移动的石头小于等于M,则此解可行。
ans = m;
l = m + 1;//**为什么不是l = m?** 这里又涉及偏向的问题。
}
else {
//如果以m为答案移动的石头数大于限定值M,则此解m太大,非法,向左找
r = m - 1;
}
}
cout << ans;
return 0;
}二分的有关知识和思考就写到这里啦!大家多写题,多思考,多进步!❛‿˂̵✧
欢迎指出错误和友好讨论~