作者丨苏剑林

单位丨追一科技

研究方向丨NLP，神经网络

个人主页丨kexue.fm

前些天刷 arXiv 看到新文章 Self-Orthogonality Module: A Network Architecture Plug-in for Learning Orthogonal Filters（下面简称“原论文”），看上去似乎有点意思，于是阅读了一番，读完确实有些收获，在此记录分享一下。 

给全连接或者卷积模型的核加上带有正交化倾向的正则项，是不少模型的需求，比如大名鼎鼎的 BigGAN 就加入了类似的正则项。而这篇论文则引入了一个新的正则项，笔者认为整个分析过程颇为有趣，可以一读。

为什么希望正交？

在开始之前，我们先约定：本文所出现的所有一维向量都代表列向量。那么，现在假设有一个 d 维的输入样本 ，经过全连接或卷积层时，其核心运算就是：

其中  是一个矩阵，它就被称“核”（全连接核/卷积核），而  是该矩阵的各个列向量。上式也可以写成：

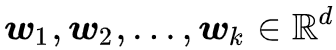
直观来看，可以认为  代表了 k 个不同的视角，而 y 就是 x 在这 k 个视角之下的观测结果。

既然有 k 个视角，那么为了减少视角的冗余（更充分的利用所有视角的参数），我们自然是希望各个视角互不相关（举个极端的例子，如果有两个视角一模一样的话，那这两个视角取其一即可）。而对于线性空间中的向量来说，不相关其实就意味着正交，所以我们希望：

这便是正交化的来源。

常见的正交化方法

矩阵的正交化跟向量的归一化有点类似，但是难度很不一样。对于一个非零向量 w 来说，要将它归一化，只需要 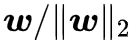 就行了，但矩阵正交化并没有类似手段。读者可能会想到“格拉姆-施密特正交化”，但这个计算成本有点大，而且它的不对称性也是一个明显的缺点。 

当然，一般来说我们也不是非得要严格的正交，所以通常的矩阵正交化的手段其实是添加正交化相关的正则项，比如对于正交矩阵来说我们有 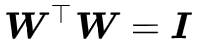，所以我们可以添加正则项：

这里的范数 ||⋅|| 可以用矩阵 2 范数或矩阵 F 范数（关于矩阵范数的概念，可以参考深度学习中的Lipschitz约束：泛化与生成模型）。