分离与联合:一种用于小样本学习的简单元迁移方法
引用:Zheng Y, Zhang X, Tian Z, et al. Detach and unite: A simple meta-transfer for few-shot learning[J]. Knowledge-Based Systems, 2023, 277: 110798.
论文地址:下载地址
论文代码:https://github.com/yaoyz96/a-met
Abstract
小样本学习(Few-shot Learning, FSL)是一个具有挑战性的问题,旨在从有限的示例中学习并进行泛化。最近的研究采用了元学习和迁移学习策略的结合来解决 FSL 任务。这些方法执行预训练,并将学到的知识转移到元学习中。然而,这种迁移模式是否适当尚不明确,且这两种学习策略的目标尚未得到充分探讨。此外,FSL 中元学习的推理依赖于样本关系,而这些关系需要进一步考虑。在本文中,我们揭示了预训练与元学习策略之间一个被忽视的学习目标差异,并提出了一种简单但有效的小样本分类任务学习范式。具体来说,提出的方法包含两个组成部分:(i)分离:我们提出了一种有效的学习范式,称为自适应元迁移(Adaptive Meta-Transfer, A-MET),该方法通过自适应地消除预训练中学到的不期望的表示,来解决这一差异。(ii)联合:我们提出了一种全局相似性兼容性度量(Global Similarity Compatibility Measure, GSCM),以在全局水平上联合考虑样本之间的关联,从而实现更一致的预测。所提出的方法简单易于实现,无需复杂的组件。在四个公共基准数据集上的大量实验表明,面对基类和新类之间存在较大域差异以及支持信息较少的更具挑战性的场景,我们的方法优于其他最新的先进方法。代码可在以下链接获得:https://github.com/yaoyz96/a-met。
1. Introduction
人类能够从少量的示例中学习一个概念,并将其推广到新的情境中。例如,一个孩子可以仅凭一张图片轻松地掌握“斑马”的概念。然而,尽管在许多视觉识别任务中取得了令人瞩目的成果,深度学习方法仍然无法像人类那样进行学习。受到人类学习能力的启发,小样本学习(Few-shot Learning, FSL)1 被提出,旨在模仿这种泛化能力,从极少量的标记样本中学习新概念,这使得深度学习方法更加具有挑战性,并且经常导致过拟合。近年来,许多研究探索了小样本学习在不同领域中的应用,如图像分类2、目标检测3 和语义分割4。这些工作旨在提高深度学习模型在更现实场景中的表现。
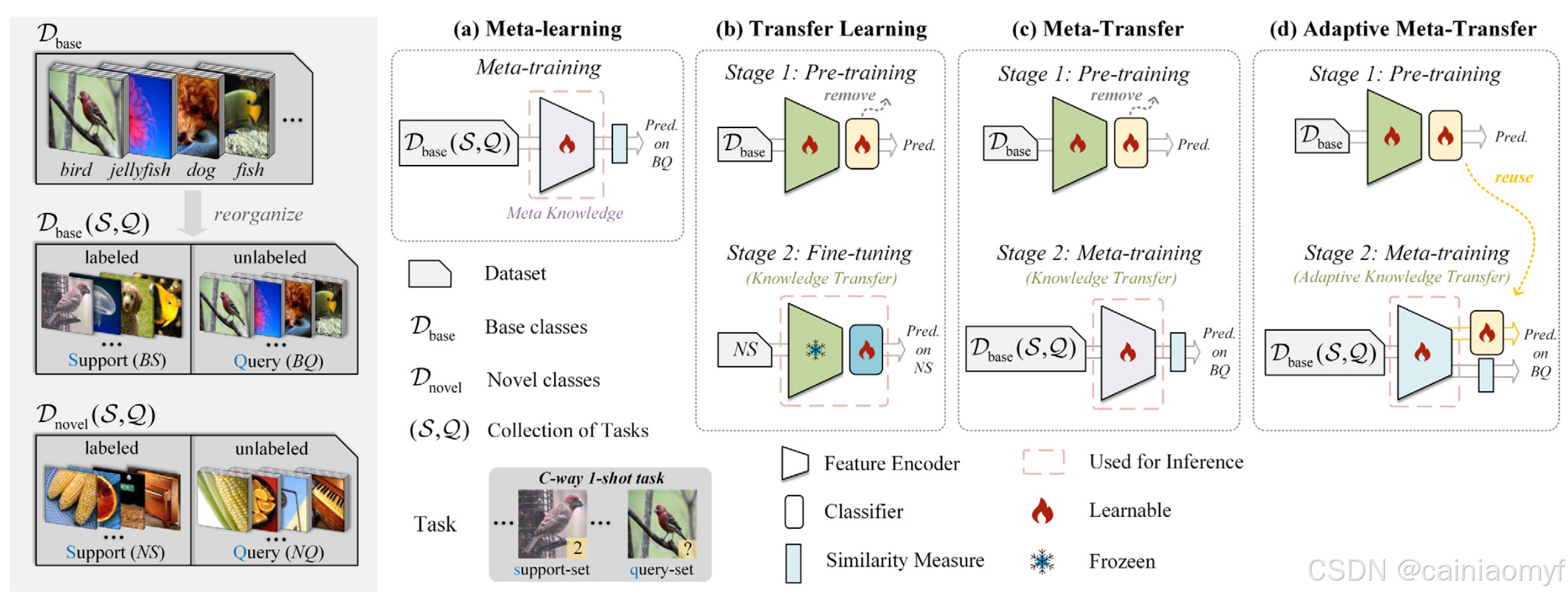
图1 小样本学习策略概述:(a)元学习,训练数据是任务的集合(
S
,
Q
S, Q
S,Q),而不是数据本身。模型经过优化,能够在
D
base
(
S
,
Q
)
D_{\text{base}}(S, Q)
Dbase(S,Q) 上表现良好,并获得在
D
novel
(
S
,
Q
)
D_{\text{novel}}(S, Q)
Dnovel(S,Q) 上的泛化能力(元知识)。(b)迁移学习,涉及在足够的例子
D
base
D_{\text{base}}
Dbase 上对模型进行预训练。然后冻结特征编码器,并使用带标记的新类数据 (
N
S
NS
NS) 微调一个新的分类器,从而对未标记的新类数据 (
N
Q
NQ
NQ) 进行预测。(c)元迁移学习结合了元学习和迁移学习策略。在预训练阶段后,移除分类器,并对特征编码器进行元训练,使其能够在各种任务上获取元知识。(d)所提出的自适应元迁移学习不同于元迁移学习,分类器在元训练阶段用于消除领域偏差。通过在两分支架构中使用对抗学习方法,特征编码器能够自适应地消除偏差,从而提高迁移能力。
通过少量的标记示例,原则上我们可以训练一个分类器为每个未标记的示例分配一个类别标签。但由于标记数据的稀缺,分类器通常容易过拟合。一种实际的解决方法是应用迁移学习5 6 7 来缓解这一问题。基本思路是先在足够的样本(基类 D base D_{\text{base}} Dbase)上预训练一个模型,然后在目标任务上微调模型,以学习未见的类别(新类 D novel D_{\text{novel}} Dnovel)。但在实践中,由于数据稀缺,大多数工作不得不冻结特征编码器,仅在 D novel D_{\text{novel}} Dnovel 上训练一个新的分类器8 9 10。小样本学习中的迁移学习策略如图1左上角所示。一些工作611 认为这种策略可以在小样本学习中达到令人满意的性能。然而,他们的预训练基类通常与新类属于同一领域。最近的工作 BiT12 提出,利用大规模标记数据(例如 ImageNet-1k 或 ImageNet-22k13),预训练模型可以为新类获得更为广泛的表示。但这意味着它需要更多的计算资源。
“学会学习”14 是构成元学习的关键思想,元学习是小样本学习中的另一种流行学习策略。元学习为小样本学习定义了一种学习机制,通常称为“情境学习”。与标准深度学习不同,情境学习的训练/测试数据是任务( S S S, Q Q Q)的集合,而不是数据本身。在每个任务中,我们可以随机选择 C C C 个独特的类别,每个类别有 K K K 个标记样本(支持集 S S S)和 N N N 个未标记样本(查询集 Q Q Q)。 Q Q Q 的预测基于 S S S。通常,对于由 C C C 个类别组成的任务,每个类别的 K K K 个支持样本被通常形式化为 C C C-way K K K-shot 任务。模型通过在 D base ( S , Q ) D_{\text{base}}(S, Q) Dbase(S,Q) 上进行优化,来获取在 D novel ( S , Q ) D_{\text{novel}}(S, Q) Dnovel(S,Q) 上各种任务中的泛化能力(元知识)。小样本学习中的元学习策略如图1右上角所示。受益于这种学习机制,元学习成为小样本学习中的一种有前途的方法1516,它使模型能够快速适应不同的场景。
受这两种学习策略的启发,一些研究17181920 提出,元学习与迁移学习的结合成为一种更强的小样本学习(FSL)范式。我们将这种两阶段的学习范式称为元迁移(Meta-Transfer)。具体来说,他们首先预训练一个标准的分类网络,即带有线性分类器的特征编码器,以获得具有可迁移性的收敛特征编码器。然后直接移除线性分类器,并对特征编码器进行元训练以执行各种任务。然而,由于可用的预训练或支持样本有限,该范式的性能仍然受到影响。我们对学到的特征编码器进行了情境推理,发现了两个主要的误分类原因。首先,模型往往集中在小而不完整的特征上,这会对小样本任务中查询样本与支持样本之间的相似性测量产生负面影响。我们将这一现象归因于由于分类器存在而产生的实例特定偏差。其次,支持信息越少,模型区分样本之间共性的难度越大。我们认为,不同的学习策略会导致两种模型目标之间的差异,并自然引起嵌入间的差距。预训练的特征编码器与线性分类器共同执行分类任务,从而限制了它的表示质量。此外,情境推理是基于查询样本与支持样本之间的共性,因此独立地表示样本并不是最优的。
在这项工作中,我们探讨了迁移学习和元学习策略合作的深层见解。基于小样本分类(FSC)任务,我们揭示了这两种策略之间一个被忽视的学习目标差异。与广泛使用的元迁移方法1921 相比,我们关注目标差异,旨在分离预训练过程中学到的不完整的无用表示。为此,我们提出了一种两分支的学习范式,自适应元迁移(Adaptive Meta-Transfer,A-MET),以自适应地消除不完整的表示,从而获得更强的特征嵌入和更好的可迁移性。元迁移和自适应元迁移的学习策略如图1所示。
此外,我们分析了预测机制,并提出了一种新的全局相似性兼容性度量(Global Similarity Compatibility Measure,GSCM),通过联合重新嵌入样本表示,使查询样本和支持样本之间的预测结果更加一致。与 RelationNet22 和 CANet23 不同,GSCM 从全局层面考虑样本之间的关联,从而减少了噪声的可能性。GSCM 不引入额外的参数,同时高效地促进了基于度量的元学习。
我们在流行的 miniImageNet 1、tiered-ImageNet 24、Omniglot 25 和 CUB 26 数据集上进行了全面的实验。实验结果表明,所提出的方法在基类与新类之间存在较大域差异、可用的支持信息较少的情况下,具有更多优势。
我们的贡献总结如下:
- 我们首次探索了迁移学习与元学习策略合作背后的深层见解,并揭示了一个被忽视但重要的学习目标差异。与广泛使用的学习范式相比,我们提出了一种适用于任意网络架构的小样本分类(FSC)的简单但有效的学习范式。
- 我们提出了一种有效的学习范式 A-MET,用于学习更强的特征嵌入,具有更好的可迁移性。A-MET 自适应地消除了预训练阶段学到的不完整表示,解决了两种学习策略之间的目标差异,在基类与新类之间存在较大域差异的情况下,表现出更大的优势。
- 我们提出了一种简单的表示度量 GSCM,通过联合重新嵌入样本表示来表示样本,使相关样本的预测结果更加一致。GSCM 从全局层面考虑样本关联,从而减少了噪声的可能性,在可用支持信息较少的情况下,具有更多的优势。
2. Related work
2.1 Transfer learning for FSL
迁移学习27 在许多任务中取得了巨大的成功,尤其是在可用数据有限的情况下。最近的研究将迁移学习应用于小样本学习(FSL)任务5 6 7。通常,他们会在足够的样本(基类 D base D_{\text{base}} Dbase)上进行预训练,然后在目标任务上微调模型,以学习未见的类别(新类 D novel D_{\text{novel}} Dnovel)。具体来说,他们通过最小化交叉熵损失,从头开始预训练特征编码器 f θ f_\theta fθ 和分类器 C ( ⋅ ∣ W b ) C(\cdot|W_b) C(⋅∣Wb)。给定预训练的特征编码器后,他们会附加一个新的分类器 C ( ⋅ ∣ W n ) C(\cdot|W_n) C(⋅∣Wn),并使用少量的新类样本微调网络。在微调阶段,由于新类数据的稀缺性,他们不得不冻结特征编码器,只训练一个新的分类器8 9 10。然而,他们的预训练基类通常与新类属于相同的领域。在实际应用中,这种情况很少满足,因为基类和新类之间往往存在较大的领域差距。
2.2 Meta-learning for FSL
元学习是小样本学习(FSL)的事实标准框架1 28。它的核心是训练一个元学习者在一组任务(称为“情境”)上,以提取能够转移到数据稀少的新任务上的元知识。许多针对小样本学习的元学习架构已经被提出,包括基于记忆的方法29 30 31、基于优化的方法9 32 33 和基于度量的方法1。
目前,基于度量的方法已经成为小样本学习的主流方法。经典的工作 Prototypical Networks28 提出了计算支持集中的每个类别的平均特征,作为该类别的原型。查询样本的分类是通过计算每个原型与查询样本之间的相似性来完成的。具体来说,他们通过嵌入函数 f θ : R D → R M f_\theta : \mathbb{R}^D \to \mathbb{R}^M fθ:RD→RM 为每个支持样本计算一个 M M M 维的特征嵌入,其中 θ \theta θ 是可学习的参数。原型是属于该类别的 K K K 个支持样本的平均特征向量。然而,在更具现实性的 1-shot 情况下,性能严重下降。
一个直观的原因是预测缺乏足够的支持信息。另一个被大多数研究忽视的潜在原因是推理过程对无关特征很脆弱。具体来说,神经网络无法区分当前任务中的关键信息,因为每个样本都是独立处理的。一些工作已经关注到这个问题22 23 34,它们致力于设计具有更大容量的复杂网络,以更好地专注于共同特征。RelationNet22 提出了一种关系模块,作为一个可学习的度量,与深度表示一起训练。CANet23 提出了一种交叉注意力网络,为每对原型和查询样本生成注意力图。ArL34 提出了为关系学习学习对象类别概念。RENet35 提出了一种关系嵌入机制,能够从不同类别之间的关系中进行学习。然而,它们仅在局部水平上考虑样本的关联,这在跨域任务中仍然会受到较大方差的影响。与之前的工作不同,我们提出了一种简单的度量 GSCM,以从全局层面联合表示样本,从而实现更一致的预测。GSCM 不引入额外的参数,同时高效地促进了基于度量的元学习。
2.3. Meta-transfer
许多研究17 19 已经表明,与从头开始进行元学习相比,通过预训练并将所学知识转移到元学习中,可以学到更强的表示,从而推广到新任务。在这些方法中,首先预训练一个标准的分类网络,以获得一个收敛的特征编码器。随后,移除线性分类器,对特征编码器进行元训练,以执行各种任务。这个学习范式可以称为元迁移(Meta-Transfer, MET)。然而,这种迁移模式是否合适尚不明确,还需要进一步讨论。
Meta-Baseline19 从基类和新类的泛化能力角度描述并评估了预训练和元学习之间的冲突。IFSL36 从结构因果的角度解释了预训练模型的局限性。他们认为,预训练的知识是一个混杂因素,限制了元学习的表现。然而,他们都没有关注两种学习策略之间的目标差异及其解决方案。CAE37 认为线性层会限制特征编码器的能力,从而对下游任务产生负面影响。他们的观点与我们相似,但尚未在小样本学习领域得到验证。
与上述工作不同,我们特别关注预训练和元学习之间被忽视但重要的目标差异问题,旨在弥合这一差距,以获得更强的特征嵌入和更好的可迁移性。LNL38 提出了一种正则化算法,以约束模型从偏置数据中学习,明确定义了不应学习的不期望属性。受 LNL 的启发,我们提出了一种有效的学习范式,自适应地消除不期望的表示,以解决两种训练策略之间的学习目标差异。与 LNL 不同,所提出的学习范式不需要明确定义监督属性,并且可以应用于任意的网络架构。
3. Method
3.1. Task formulation
我们考虑小样本分类(FSC)任务。形式上,我们有一个基类集合 D base D_{\text{base}} Dbase(训练集)和一个新类集合 D novel D_{\text{novel}} Dnovel(测试集),其中 D base ∩ D novel = ∅ D_{\text{base}} \cap D_{\text{novel}} = \emptyset Dbase∩Dnovel=∅。FSC 的目标是从 D base D_{\text{base}} Dbase 学习并推广到 D novel D_{\text{novel}} Dnovel。此外, D novel D_{\text{novel}} Dnovel 只有少量已标记的数据,称为支持集(support-set),其余未标记的数据称为查询集(query-set)。我们可以从 D base D_{\text{base}} Dbase 中学习知识,并在 D novel D_{\text{novel}} Dnovel 上进行测试。
按照两阶段的学习范式,我们首先以标准监督方式从
D
base
D_{\text{base}}
Dbase 编码可迁移的知识(即预训练)。我们从头开始在
D
base
D_{\text{base}}
Dbase 上训练一个特征编码器
f
θ
f_\theta
fθ 和一个线性分类器
l
ϕ
l_\phi
lϕ。形式上,我们将学习的模型表示为
P
ϕ
(
y
∣
x
;
θ
)
P_\phi(y|x; \theta)
Pϕ(y∣x;θ),其中
x
x
x 是输入数据,
y
y
y 是数据标签,
ϕ
\phi
ϕ 和
θ
\theta
θ 分别是线性分类器和特征编码器的参数。我们将
L
y
(
x
;
θ
,
ϕ
)
L_y(x; \theta , \phi)
Ly(x;θ,ϕ) 作为损失函数,将
E
(
f
θ
,
l
ϕ
)
E(f_\theta , l_\phi )
E(fθ,lϕ) 作为
P
ϕ
(
y
∣
x
;
θ
)
P_\phi(y|x; \theta)
Pϕ(y∣x;θ) 的目标函数,模型可以通过以下方式优化:
E
(
f
θ
,
l
ϕ
)
=
1
N
∑
i
=
1
N
L
y
(
x
i
;
θ
,
ϕ
)
,
(1)
E(f_\theta , l_\phi ) = \frac{1}{N} \sum_{i=1}^N L_y(x_i; \theta, \phi),\tag{1}
E(fθ,lϕ)=N1i=1∑NLy(xi;θ,ϕ),(1)
其中
N
N
N 表示一个批次中的样本数。样本
x
x
x 的损失函数
L
y
L_y
Ly 可以定义为:
L
y
=
−
log
exp
(
p
k
(
x
)
)
∑
j
exp
(
p
j
(
x
)
)
,
(2)
L_y = -\log \frac{\exp(p_k(x))}{\sum_j \exp(p_j(x))},\tag{2}
Ly=−log∑jexp(pj(x))exp(pk(x)),(2)
其中
p
j
(
x
)
=
l
ϕ
(
f
θ
(
x
)
)
[
j
]
p_j(x) = l_\phi(f_\theta(x))[j]
pj(x)=lϕ(fθ(x))[j] 表示分类器对输入样本
x
x
x 的第
j
j
j 类别的对数值。我们旨在最小化目标函数并找到最佳参数,以确保整体良好的预测结果:
ϕ
^
,
θ
^
←
arg
min
ϕ
,
θ
E
(
f
θ
,
l
ϕ
)
.
(3)
\hat{\phi}, \hat{\theta} \leftarrow \arg \min_{\phi, \theta} E(f_\theta , l_\phi).\tag{3}
ϕ^,θ^←argϕ,θminE(fθ,lϕ).(3)
在元训练阶段,情境被设计用来模拟元测试中的设置。具体来说,
D
base
D_{\text{base}}
Dbase 被重新组织为训练情境
{
(
S
i
,
Q
i
)
}
\{(S_i, Q_i)\}
{(Si,Qi)}。每个情境通过从
D
base
D_{\text{base}}
Dbase 中随机选择
C
C
C 个类别构成,并且其支持集为
S
i
=
{
(
x
s
(
i
)
,
y
s
(
i
)
)
∣
y
s
(
i
)
∈
D
base
}
i
=
1
C
×
K
,
S_i = \{(x_s^{(i)}, y_s^{(i)}) | y_s^{(i)} \in D_{\text{base}}\}_{i=1}^{C \times K},
Si={(xs(i),ys(i))∣ys(i)∈Dbase}i=1C×K,,其中每个类别包含
K
K
K 个标记样本。其余的
C
C
C 类别中的
Q
Q
Q 个样本作为查询集
Q
i
=
{
(
x
q
(
i
)
,
y
q
(
i
)
)
∣
y
q
(
i
)
∈
D
base
}
i
=
1
C
×
Q
.
Q_i = \{(x_q^{(i)}, y_q^{(i)}) | y_q^{(i)} \in D_{\text{base}}\}_{i=1}^{C \times Q}.
Qi={(xq(i),yq(i))∣yq(i)∈Dbase}i=1C×Q.学习到的特征编码器
f
θ
f_\theta
fθ 将每个支持集
S
i
S_i
Si 映射到一个嵌入空间,在该空间中每个类别由一个原型
c
k
∈
R
M
c_k \in \mathbb{R}^M
ck∈RM 表示,原型由该类别的示例围绕。
M
M
M 是由
f
θ
f_\theta
fθ 嵌入的特征维度。类别
k
k
k 的原型
c
k
c_k
ck 定义为该类别中所有嵌入的支持样本的平均值:
c
k
=
1
∣
S
k
∣
∑
(
x
i
,
y
i
)
∈
S
k
f
θ
(
x
i
)
,
(4)
c_k = \frac{1}{|S_k|} \sum_{(x_i, y_i) \in S_k} f_\theta(x_i),\tag{4}
ck=∣Sk∣1(xi,yi)∈Sk∑fθ(xi),(4)
其中
S
k
S_k
Sk 表示来自类别
k
k
k 的支持样本。
给定相似度度量函数
m
:
R
M
→
R
C
m : \mathbb{R}^M \to \mathbb{R}^C
m:RM→RC,其中
C
C
C 是一个情境中的类别数,对于查询样本的类别概率分布可以定义为:
p
(
y
=
k
∣
x
)
=
exp
(
−
m
(
f
θ
(
x
)
,
c
k
)
)
∑
k
′
=
1
C
exp
(
−
m
(
f
θ
(
x
)
,
c
k
′
)
)
.
(5)
p(y = k | x) = \frac{\exp(-m(f_\theta(x), c_k))}{\sum_{k'=1}^C \exp(-m(f_\theta(x), c_{k'}))}.\tag{5}
p(y=k∣x)=∑k′=1Cexp(−m(fθ(x),ck′))exp(−m(fθ(x),ck)).(5)
3.2. Adaptive meta-transfer
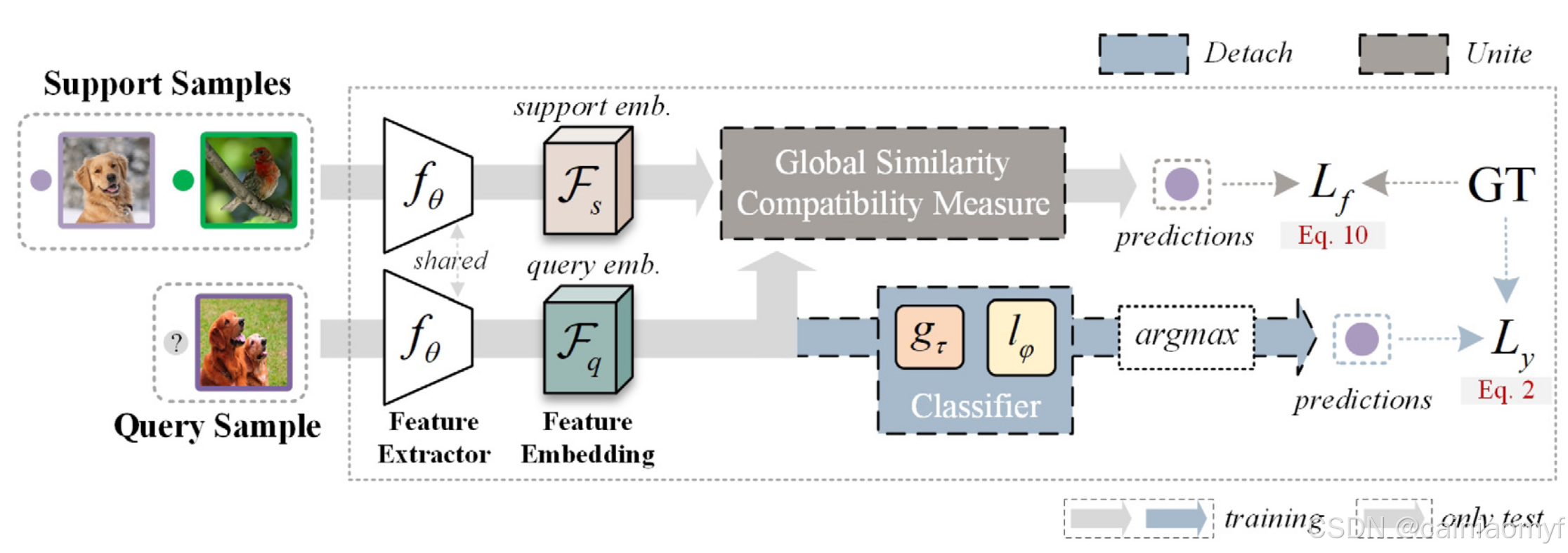
由于预训练样本的有限性,预训练模型不可避免地倾向于实例特定的偏差,这阻碍了其向新类别的迁移能力。我们的目标是训练一个特征编码器 f θ f_\theta fθ,专注于更一般的特征,从而在未见的新类上表现良好。特征编码器可以通过公式 (1) 在预训练阶段进行优化。在这一节中,我们重点介绍元学习阶段。图 2 展示了提出的学习范式的元学习阶段,我们将这种双分支架构称为自适应元迁移(Adaptive Meta-Transfer)。
图2 所提出的学习范式 “Detach and Unite” 的元学习阶段概述。特征编码器 f θ f_\theta fθ 和线性层 l ϕ l_\phi lϕ 来源于预训练阶段。 g τ g_\tau gτ 是一个带有参数 τ \tau τ 的梯度反转层。‘‘L’’ 和 ‘‘GT’’ 分别代表损失函数和真实标签(ground truth)。我们没有明确指定详细的架构,因为所提出的学习范式可以应用于任意网络架构。
训练数据
D
base
D_{\text{base}}
Dbase 和测试数据
D
novel
D_{\text{novel}}
Dnovel 都具有复杂且未知的分布,分别记为
U
(
x
)
U(x)
U(x) 和
V
(
x
)
V(x)
V(x)。我们将数据集
D
D
D 中的实例特定偏差定义为
B
B
B。假设
B
B
B 包含
D
D
D 可以拥有的所有可能的目标偏差
b
(
⋅
)
b(\cdot)
b(⋅),其中
b
:
D
→
B
b: D \to B
b:D→B。预训练阶段确保了特征编码器
f
θ
f_\theta
fθ 和线性分类器
l
ϕ
l_\phi
lϕ 在
U
(
x
)
U(x)
U(x) 上的组合具有整体良好的预测性能,其学习目标为:
O
⟨
f
θ
,
l
ϕ
⟩
:
l
ϕ
(
f
θ
(
x
)
)
∼
U
(
x
)
,
(6)
O \langle f_\theta , l_\phi \rangle : l_\phi (f_\theta (x)) \sim U(x),\tag{6}
O⟨fθ,lϕ⟩:lϕ(fθ(x))∼U(x),(6)
其中
⟨
⋅
⟩
\langle \cdot \rangle
⟨⋅⟩ 表示综合优化目标。然而,
U
(
x
)
U(x)
U(x) 同时包含领域不变和领域特定的特征(即偏差)。因此,特征编码器
f
θ
f_\theta
fθ 不可避免地倾向于偏差,其学习目标可以表示为:
O
⟨
f
θ
⟩
:
f
θ
(
x
)
∼
I
(
x
)
+
B
U
(
x
)
,
(7)
O \langle f_\theta \rangle : f_\theta (x) \sim I(x) + B_U(x),\tag{7}
O⟨fθ⟩:fθ(x)∼I(x)+BU(x),(7)
其中
I
(
x
)
I(x)
I(x) 是领域不变特征分布,
B
U
(
x
)
B_U(x)
BU(x) 是
U
(
x
)
U(x)
U(x) 上的领域特定特征分布。我们的目标是从
f
θ
f_\theta
fθ 中分离出由
⟨
f
θ
,
l
ϕ
⟩
\langle f_\theta , l_\phi \rangle
⟨fθ,lϕ⟩ 学到的
B
U
(
x
)
B_U(x)
BU(x),并使其满足:
O
⟨
f
θ
⟩
→
O
′
⟨
f
θ
⟩
,
w
h
e
r
e
O
′
⟨
f
θ
⟩
:
f
θ
(
x
)
∼
I
(
x
)
,
(8)
O \langle f_\theta \rangle \to O' \langle f_\theta \rangle, where O' \langle f_\theta \rangle : f_\theta (x) \sim I(x), \tag{8}
O⟨fθ⟩→O′⟨fθ⟩,whereO′⟨fθ⟩:fθ(x)∼I(x),(8)
显式地测量
B
U
(
x
)
B_U(x)
BU(x) 并不容易。预训练阶段中
f
θ
f_\theta
fθ 和
l
ϕ
l_\phi
lϕ 的协同作用启发了我们的想法。我们致力于在元训练阶段减少
l
ϕ
l_\phi
lϕ 对
f
θ
f_\theta
fθ 的影响。具体来说,
f
θ
f_\theta
fθ 和
l
ϕ
l_\phi
lϕ 的组合在预训练阶段通过最小化公式 (2) 中定义的损失函数
L
y
L_y
Ly,从
I
(
x
)
I(x)
I(x) 和
B
U
(
x
)
B_U(x)
BU(x) 中学习。在元学习阶段,
f
θ
f_\theta
fθ 进一步训练以在
U
(
x
)
U(x)
U(x) 上提供一致的预测。因此,我们的目标是在最大化分类器
l
ϕ
l_\phi
lϕ 的损失
L
y
L_y
Ly 的同时,找到最小化损失
L
f
L_f
Lf 的参数
θ
\theta
θ。在实际操作中,我们通过对抗策略联合训练
f
θ
f_\theta
fθ 和
l
ϕ
l_\phi
lϕ,并且优化目标可以通过参数化为
τ
\tau
τ 的梯度反转层
g
τ
g_\tau
gτ 实现。因此,
f
θ
f_\theta
fθ 和
l
ϕ
l_\phi
lϕ 可以通过以下方式迭代优化:
f
θ
^
←
⟨
∇
L
f
,
−
τ
∇
L
y
⟩
,
(9a)
\hat{f_\theta} \leftarrow \langle \nabla L_f, -\tau \nabla L_y \rangle, \tag{9a}
fθ^←⟨∇Lf,−τ∇Ly⟩,(9a)
l
ϕ
^
←
⟨
∇
L
y
⟩
,
(9b)
\hat{l_\phi} \leftarrow \langle \nabla L_y \rangle, \tag{9b}
lϕ^←⟨∇Ly⟩,(9b)
其中
L
y
L_y
Ly 表示公式 (2) 中定义的损失函数,
L
f
L_f
Lf 可以定义为公式 (5) 中概率分布
p
(
y
∣
x
)
p(y|x)
p(y∣x) 的交叉熵损失:
L
f
=
−
log
exp
(
−
m
(
f
θ
(
x
)
,
c
k
)
)
∑
k
′
=
1
C
exp
(
−
m
(
f
θ
(
x
)
,
c
k
′
)
)
=
−
log
p
(
y
=
k
∣
x
)
.
(10)
L_f = -\log \frac{\exp(-m(f_\theta(x), c_k))}{\sum_{k'=1}^{C} \exp(-m(f_\theta(x), c_{k'}))} = -\log p(y=k|x). \tag{10}
Lf=−log∑k′=1Cexp(−m(fθ(x),ck′))exp(−m(fθ(x),ck))=−logp(y=k∣x).(10)
梯度反转层的前向和反向传播可以定义为:
g
τ
(
x
)
=
x
,
d
g
τ
d
x
=
−
τ
I
,
(11)
g_\tau(x) = x, \quad \frac{dg_\tau}{dx} = -\tau I, \tag{11}
gτ(x)=x,dxdgτ=−τI,(11)
其中
τ
\tau
τ 是梯度反转层的常数超参数,
I
I
I 是单位矩阵。因此,最终的目标函数可以表示为:
E
~
(
f
θ
,
l
ϕ
)
=
1
N
e
(
∑
i
=
1
N
e
L
f
(
h
(
m
(
f
θ
(
x
i
;
θ
)
,
c
i
)
)
,
y
i
)
+
∑
i
=
1
N
e
L
y
(
l
ϕ
(
g
τ
(
f
θ
(
x
i
;
θ
)
;
−
τ
)
;
ϕ
)
,
y
i
)
)
=
1
N
e
(
∑
i
=
1
N
e
L
f
i
(
x
;
θ
)
+
∑
i
=
1
N
e
L
y
i
(
x
;
θ
,
ϕ
,
τ
)
)
\tilde{E}(f_\theta, l_\phi) = \frac{1}{N_e} \left( \sum_{i=1}^{N_e} L_f(h(m(f_\theta(x_i; \theta), c_i)), y_i) + \sum_{i=1}^{N_e} L_y(l_\phi(g_\tau(f_\theta(x_i; \theta); -\tau); \phi), y_i) \right) = \frac{1}{N_e} \left( \sum_{i=1}^{N_e} L^i_f(x; \theta) + \sum_{i=1}^{N_e} L^i_y(x; \theta, \phi, \tau) \right)
E~(fθ,lϕ)=Ne1(i=1∑NeLf(h(m(fθ(xi;θ),ci)),yi)+i=1∑NeLy(lϕ(gτ(fθ(xi;θ);−τ);ϕ),yi))=Ne1(i=1∑NeLfi(x;θ)+i=1∑NeLyi(x;θ,ϕ,τ))
其中
N
e
N_e
Ne 是情境的数量,
h
(
⋅
)
h(\cdot)
h(⋅) 是将相似度矩阵映射到预测的映射函数,
m
m
m 是公式 (3) 中描述的相似度度量,
c
c
c 是公式 (2) 中定义的类别原型。
f
θ
f_\theta
fθ 和
l
ϕ
l_\phi
lϕ 可以通过以下函数迭代优化(学习率为
α
\alpha
α):
ϕ
^
,
θ
^
←
arg
min
ϕ
,
θ
E
~
(
f
θ
,
l
ϕ
)
,
(13a)
\hat{\phi}, \hat{\theta} \leftarrow \arg \min_{\phi,\theta} \tilde{E}(f_\theta, l_\phi), \tag{13a}
ϕ^,θ^←argϕ,θminE~(fθ,lϕ),(13a)
θ
^
←
θ
−
α
(
∂
L
f
∂
θ
−
τ
∂
L
y
∂
θ
)
,
(13b)
\hat{\theta} \leftarrow \theta - \alpha \left( \frac{\partial L_f}{\partial \theta} - \tau \frac{\partial L_y}{\partial \theta} \right), \tag{13b}
θ^←θ−α(∂θ∂Lf−τ∂θ∂Ly),(13b)
ϕ
^
←
ϕ
−
α
∂
L
y
∂
ϕ
.
(13c)
\hat{\phi} \leftarrow \phi - \alpha \frac{\partial L_y}{\partial \phi}. \tag{13c}
ϕ^←ϕ−α∂ϕ∂Ly.(13c)
算法 1 总结了提出的学习范式。特别地, l ϕ l_\phi lϕ 是一个全连接层,专门用于联合训练阶段,并且不会影响最终性能。关键要求是确保在两个学习阶段中使用相同的 l ϕ l_\phi lϕ。
3.3. Global similarity compatibility measure
直观上,可以通过比较查询样本与每个支持原型的相似性来进行预测。然而,在更现实的 1-shot 情况下,模型的性能受到严重的影响。这可以归因于推理过程在处理无关特征时的脆弱性。换句话说,模型难以区分与当前任务相关的关键信息。具体来说,通用特征编码器
f
θ
f_\theta
fθ 将输入数据
D
D
D 映射到特征嵌入空间:
D
→
R
M
D \to \mathbb{R}^M
D→RM。每个情境可以被建模为
f
θ
(
{
x
i
}
i
=
1
N
)
f_\theta(\{x_i\}_{i=1}^N)
fθ({xi}i=1N),其中
N
=
(
K
+
Q
)
×
C
N = (K + Q) \times C
N=(K+Q)×C,特征嵌入是一个按行堆叠的矩阵
F
=
{
f
θ
(
x
i
)
}
i
=
1
N
∈
R
N
×
M
F = \{f_\theta(x_i)\}_{i=1}^N \in \mathbb{R}^{N \times M}
F={fθ(xi)}i=1N∈RN×M。因此,一个情境的特征嵌入集合可以定义为:
F
e
=
[
F
s
F
q
]
∈
R
N
×
M
,
(14)
F_e = \begin{bmatrix} F_s \\ F_q \end{bmatrix} \in \mathbb{R}^{N \times M}, \tag{14}
Fe=[FsFq]∈RN×M,(14)
其中支持集和查询集的特征嵌入可以表示为:
F
s
=
[
f
s
(
1
)
,
f
s
(
2
)
,
…
,
f
s
(
K
×
C
)
]
T
∈
R
K
×
C
×
M
,
(15a)
F_s = \begin{bmatrix} f_s^{(1)}, f_s^{(2)}, \dots, f_s^{(K \times C)} \end{bmatrix}^T \in \mathbb{R}^{K \times C \times M}, \tag{15a}
Fs=[fs(1),fs(2),…,fs(K×C)]T∈RK×C×M,(15a)
F
q
=
[
f
q
(
1
)
,
f
q
(
2
)
,
…
,
f
q
(
Q
×
C
)
]
T
∈
R
Q
×
C
×
M
,
(15b)
F_q = \begin{bmatrix} f_q^{(1)}, f_q^{(2)}, \dots, f_q^{(Q \times C)} \end{bmatrix}^T \in \mathbb{R}^{Q \times C \times M}, \tag{15b}
Fq=[fq(1),fq(2),…,fq(Q×C)]T∈RQ×C×M,(15b)
其中 f s ∈ R M f_s \in \mathbb{R}^M fs∈RM 和 f q ∈ R M f_q \in \mathbb{R}^M fq∈RM 分别表示支持样本和查询样本的特征。为了对查询集进行预测,常见的做法是计算支持原型 c k c_k ck 和查询样本 f q f_q fq 之间的相似性,其中 c k c_k ck 是在公式 (4) 中定义的支持原型。然而, F e F_e Fe 将查询和支持特征嵌入独立处理,这使得度量对由尺度、遮挡、背景等引入的噪声非常脆弱。
为了解决这个问题,我们提出在查询样本和每个支持样本之间建立全局依赖关系。通过引入全局依赖关系,模型可以考虑更全面和信息量更大的特征表示,从而基于输入的整体视图进行预测。实际操作中,我们将每个样本的特征嵌入转换为全局相似性表示
T
T
T,从空间
R
M
\mathbb{R}^M
RM 转换到
R
N
\mathbb{R}^N
RN,以构建与每个样本的相关性。转换过程可以通过
F
e
×
F
e
′
→
T
e
F_e \times F'_e \to T_e
Fe×Fe′→Te 获得。
F
e
′
F'_e
Fe′ 可以定义为:
F
e
′
=
[
F
s
′
F
q
′
]
∈
R
M
×
N
,
(16)
F'_e = \begin{bmatrix} F'_s \\ F'_q \end{bmatrix} \in \mathbb{R}^{M \times N}, \tag{16}
Fe′=[Fs′Fq′]∈RM×N,(16)
其中,
F
s
′
=
[
f
s
(
1
)
T
,
f
s
(
2
)
T
,
…
,
f
s
(
K
×
C
)
T
]
∈
R
M
×
K
×
C
,
(17a)
F'_s = \begin{bmatrix} f_s^{(1)T}, f_s^{(2)T}, \dots, f_s^{(K \times C)T} \end{bmatrix} \in \mathbb{R}^{M \times K \times C}, \tag{17a}
Fs′=[fs(1)T,fs(2)T,…,fs(K×C)T]∈RM×K×C,(17a)
F
q
′
=
[
f
q
(
1
)
T
,
f
q
(
2
)
T
,
…
,
f
q
(
Q
×
C
)
T
]
∈
R
M
×
Q
×
C
.
(17b)
F'_q = \begin{bmatrix} f_q^{(1)T}, f_q^{(2)T}, \dots, f_q^{(Q \times C)T} \end{bmatrix} \in \mathbb{R}^{M \times Q \times C}. \tag{17b}
Fq′=[fq(1)T,fq(2)T,…,fq(Q×C)T]∈RM×Q×C.(17b)
转换后的特征嵌入集合
T
e
T_e
Te 可以表示为:
T
e
=
[
T
s
T
q
]
∈
R
N
×
N
,
(18)
T_e = \begin{bmatrix} T_s \\ T_q \end{bmatrix} \in \mathbb{R}^{N \times N}, \tag{18}
Te=[TsTq]∈RN×N,(18)
其中,
T
s
=
[
t
s
(
1
)
,
t
s
(
2
)
,
…
,
t
s
(
K
×
C
)
]
T
∈
R
K
×
C
×
N
,
(19a)
T_s = \begin{bmatrix} t_s^{(1)}, t_s^{(2)}, \dots, t_s^{(K \times C)} \end{bmatrix}^T \in \mathbb{R}^{K \times C \times N}, \tag{19a}
Ts=[ts(1),ts(2),…,ts(K×C)]T∈RK×C×N,(19a)
T
q
=
[
t
q
(
1
)
,
t
q
(
2
)
,
…
,
t
q
(
Q
×
C
)
]
T
∈
R
Q
×
C
×
N
.
(19b)
T_q = \begin{bmatrix} t_q^{(1)}, t_q^{(2)}, \dots, t_q^{(Q \times C)} \end{bmatrix}^T \in \mathbb{R}^{Q \times C \times N}. \tag{19b}
Tq=[tq(1),tq(2),…,tq(Q×C)]T∈RQ×C×N.(19b)
在实际操作中,转换可以通过内积运算高效地计算。每个转换后的权重
w
(
i
,
j
)
w(i,j)
w(i,j) 表示样本
x
i
x_i
xi 和
x
j
x_j
xj 之间的相似性。样本
x
i
x_i
xi 的特征嵌入
t
(
i
)
t(i)
t(i) 可以表示为:
t
(
i
)
=
[
w
(
i
,
1
)
,
…
,
w
(
i
,
j
)
,
…
,
w
(
i
,
N
)
]
∈
R
N
×
1
,
(20)
t(i) = [w(i,1), \dots, w(i,j), \dots, w(i,N)] \in \mathbb{R}^{N \times 1}, \tag{20}
t(i)=[w(i,1),…,w(i,j),…,w(i,N)]∈RN×1,(20)
其中,当 i = j i = j i=j 时, w ( i , j ) w(i,j) w(i,j) 等于 1,表示样本与其自身的相似性。
T
e
T_e
Te 考虑了满足相似性一致性的两个样本是兼容的。换句话说,每个样本是基于其与其他样本的关系表示的。当我们说两个样本相似时,这意味着它们与其他样本共享相同的关系,而不仅仅是测量这两个样本之间的相似性。我们定义样本
x
i
x_i
xi 和
x
j
x_j
xj 之间的全局相似性兼容度量为:
C
(
x
i
,
x
j
)
=
cos
(
t
(
i
)
,
t
(
j
)
)
=
t
(
i
)
⋅
t
(
j
)
∥
t
(
i
)
∥
∥
t
(
j
)
∥
=
∑
k
=
1
N
w
(
i
,
k
)
×
w
(
k
,
j
)
∑
k
=
1
N
(
w
(
i
,
k
)
)
2
×
∑
k
=
1
N
(
w
(
k
,
j
)
)
2
.
(21)
C(x_i, x_j) = \cos(t(i), t(j)) = \frac{t(i) \cdot t(j)}{\|t(i)\|\|t(j)\|} = \frac{\sum_{k=1}^{N} w(i,k) \times w(k,j)}{\sqrt{\sum_{k=1}^{N} (w(i,k))^2} \times \sqrt{\sum_{k=1}^{N} (w(k,j))^2}}. \tag{21}
C(xi,xj)=cos(t(i),t(j))=∥t(i)∥∥t(j)∥t(i)⋅t(j)=∑k=1N(w(i,k))2×∑k=1N(w(k,j))2∑k=1Nw(i,k)×w(k,j).(21)
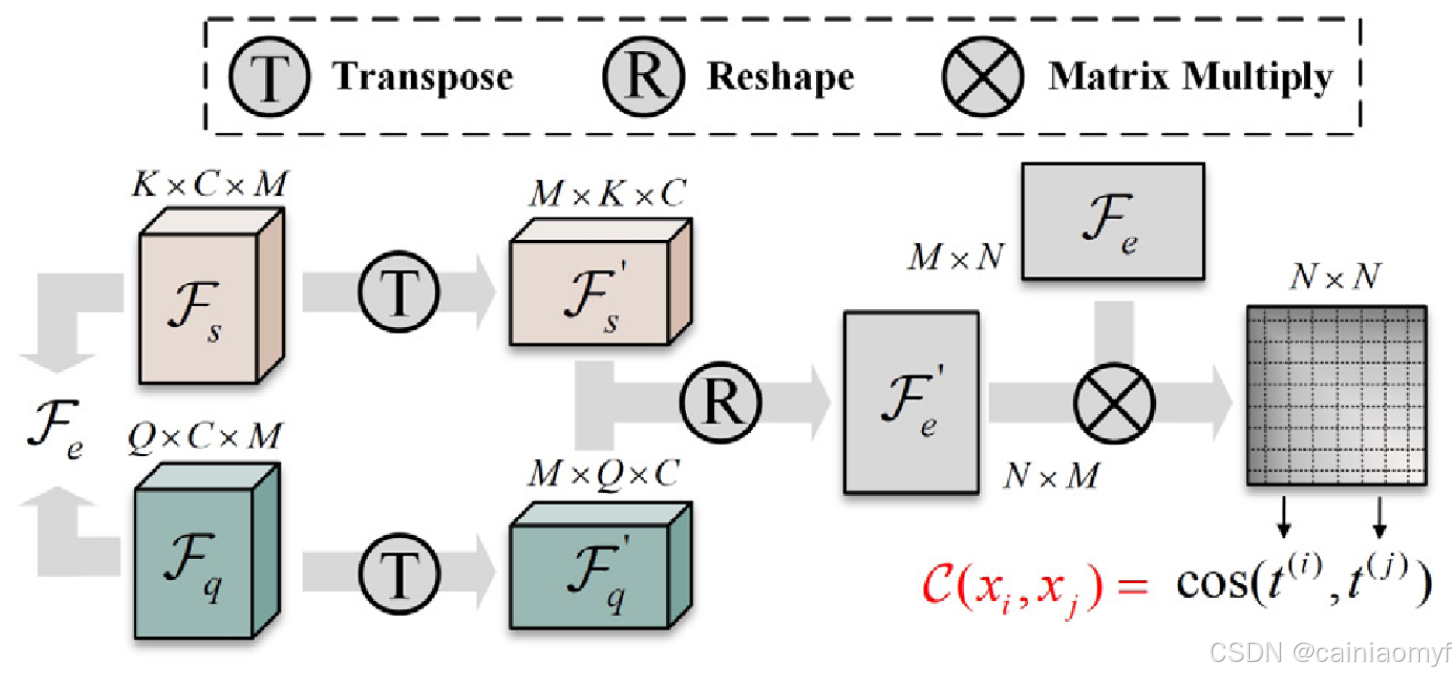
如果样本 x i x_i xi 和 x j x_j xj 是兼容的,则 C ( x i , x j ) → 1 C(x_i, x_j) \to 1 C(xi,xj)→1,并且这两个样本与其他支持样本之间的关系是一致的。GSCM 减少了噪声被包含在兼容集中的可能性,并增强了预测的鲁棒性。同时,GSCM 与特定的网络结构无关,可以应用于任何由特征编码器生成的特征。GSCM 的示意图如图 3 所示
图3 所提出的全局相似性兼容性度量的计算过程
4. Results on standard benchmarks
4.1. Datasets
- 手写字符识别任务,使用一个手写数据集 Omniglot 25。
- 通用物体识别任务,使用基于 ImageNet 39 的两个通用物体数据集,即 mini-ImageNet 1 和 tiered-ImageNet 24。
- 细粒度图像分类任务,使用一个细粒度分类数据集 CUB-200-2011 26(简称 CUB)。
Omniglot 25 是一个包含 1623 个手写字符(类别)的数据集,来自 50 种不同的字母表。每个字符包含 20 个例子,分别由不同的人书写。Omniglot 有两级层次结构,即字母表和字符。大量的类别和少量的例子使得 Omniglot 成为小样本学习的合适基准。一个常见的数据设置 128 展平并忽略了字母表和字符的两级层次结构。他们使用 1200 个字符,并通过旋转增强字符(总共 4800 个类别)进行训练,剩余字符用于测试。我们遵循这一设置来评估所提出的方法。此外,我们还遵循了原始分割 25 的设置,这更具挑战性,因为分割是在字母表级别上进行的,其中 30 个字母表用于训练,20 个用于测试。我们从训练集中保留了 5 个最小的字母表(即字符类别最少的字母表)用于验证 40。
mini-ImageNet 1 是一个用于小样本学习的通用物体识别基准,包含从 ILSVRC-2012 39 中选择的 100 个类别,每个类别包含 600 个样本。mini-ImageNet 被随机分为 64/16/20 类,用于训练、验证和测试。按照之前的工作 62041,我们在实验中使用了由 Ravi 和 Larochelle 41 提出的数据划分。
tiered-ImageNet 24 是另一个基于 ImageNet 的常用基准,其规模远大于 mini-ImageNet。它包含 608 个类别和 779,165 张来自 34 个超类别的图像。超类别被分为 20/6/8 个不相交的类别,分别导致 351 个类别用于训练,97 个类别用于验证,160 个类别用于测试。每个类别包含 1300 个样本。需要注意的是,mini-ImageNet 数据量较小,它并没有考虑基类与新类之间的相似性。而 tiered-ImageNet 的设置更具挑战性,因为基类和新类来自不同的超类别,因此 tiered-ImageNet 的训练数据和测试数据在外观和语义上有更大的差异。
Caltech-UCSD Birds-200-2011 (CUB) 26 是一个用于细粒度分类的数据集,包含 200 种不同的鸟类,总共 11,788 张图像。在实践中,我们没有使用提供的边界框来裁剪图像,而是使用原始的未裁剪图像,这带来了更大的挑战。需要注意的是,CUB 仅用于实验中的跨域评估。图 4 给出了这些数据集的一些示例。
4.2. Preprocessing and data-augmentation
为了执行小样本学习任务,有必要将每个数据集组织为一系列情境(即任务)。具体来说,每个任务通过随机选择 C C C 个类别和每个类别 K K K 个支持样本构建。对于 Omniglot,我们构建了包含 5 或 20 个类别的任务,其中每个类别只有一个支持样本。这些任务分别称为 5-way 1-shot 和 20-way 1-shot 任务。至于 mini- 和 tiered-ImageNet,我们遵循之前的工作,创建了 5-way 1-shot 和 5-way 5-shot 配置的任务。对于 CUB,我们在 1-shot 和 5-shot 场景下评估模型在 5-way 和 20-way 任务上的性能。
在实验中,应用了标准的数据增强技术,包括随机裁剪、水平翻转和颜色抖动。我们将样本大小调整为 28 × 28 用于 Omniglot,84 × 84 用于 mini-ImageNet 和 tiered-ImageNet,遵循之前的工作。
4.3. Architectures
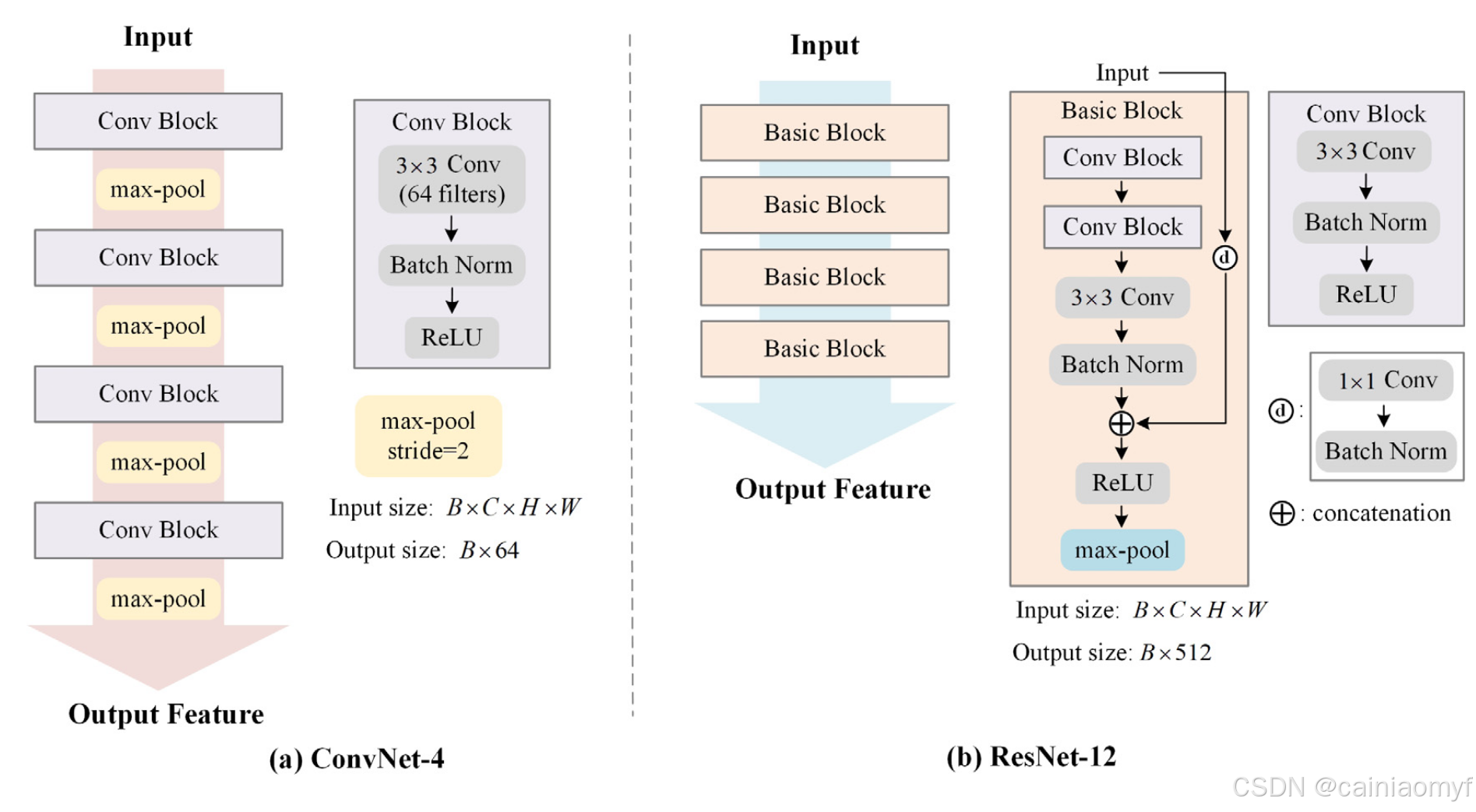
我们采用了两种常用的嵌入架构 ConvNet-4 和 ResNet-12,遵循了最近的相关工作 1928。ConvNet-4 由四个卷积块组成,每个块包含一个 64 滤波器的 3 × 3 卷积层、批归一化层和 ReLU 非线性激活。每个卷积块之后使用一个 2 × 2 的最大池化层对特征图进行下采样。ConvNet-4 的输出空间维度为 64。四个卷积块的宽度均为 64。
ResNet-12 遵循 ResNet 的架构,包含四个基本块,每个块具有三个卷积操作。每个基本块包含一个残差操作。四个阶段的基本块的宽度分别为 [64, 128, 256, 512]。每个基本块有三个 3 × 3 的卷积层,配有批归一化和 0.1 的 Leaky ReLU。在每个块的三个卷积层后,使用步幅为 2 的最大池化层。ResNet-12 的输出空间维度为 512。图 5 展示了 ConvNet-4 和 ResNet-12 的架构。
4.4. Implementation details
训练细节
我们的所有模型都通过带有 0.9 动量的 SGD 优化器进行训练。在预训练阶段,初始学习率为 0.1,衰减因子为 0.1。最大训练轮次为 100,学习率在第 90 轮时衰减。对于 Omniglot 和 mini-ImageNet,批大小为 128;对于 tiered-ImageNet,批大小为 256。在元训练阶段,初始学习率为
1
×
1
0
−
4
1 \times 10^{-4}
1×10−4,衰减因子为 0.1。我们也训练了 100 轮,每轮包含 1000 个随机采样的情境,学习率在第 40 和 80 轮时衰减。具体来说,元训练是在 5-way 1-shot 任务上进行的,每次随机选择 5 个类别,每个类别有 1 个支持样本和 15 个查询样本。所提出的 A-MET 仅引入一个额外的超参数,即公式 (11) 中梯度反转层
g
τ
g_\tau
gτ 的梯度权重
τ
\tau
τ。我们在实验中尝试了三种
τ
\tau
τ 的设置(0.1、0.3、0.5),并发现不同的设置会影响模型的收敛难度。在训练速度和准确性之间的折衷下,所有实验中
τ
\tau
τ 的值设为 0.1。对于其他超参数,权重衰减为
5
×
1
0
−
4
5 \times 10^{-4}
5×10−4。对于 tiered-ImageNet,我们在元训练阶段冻结了批归一化层。
情境评估
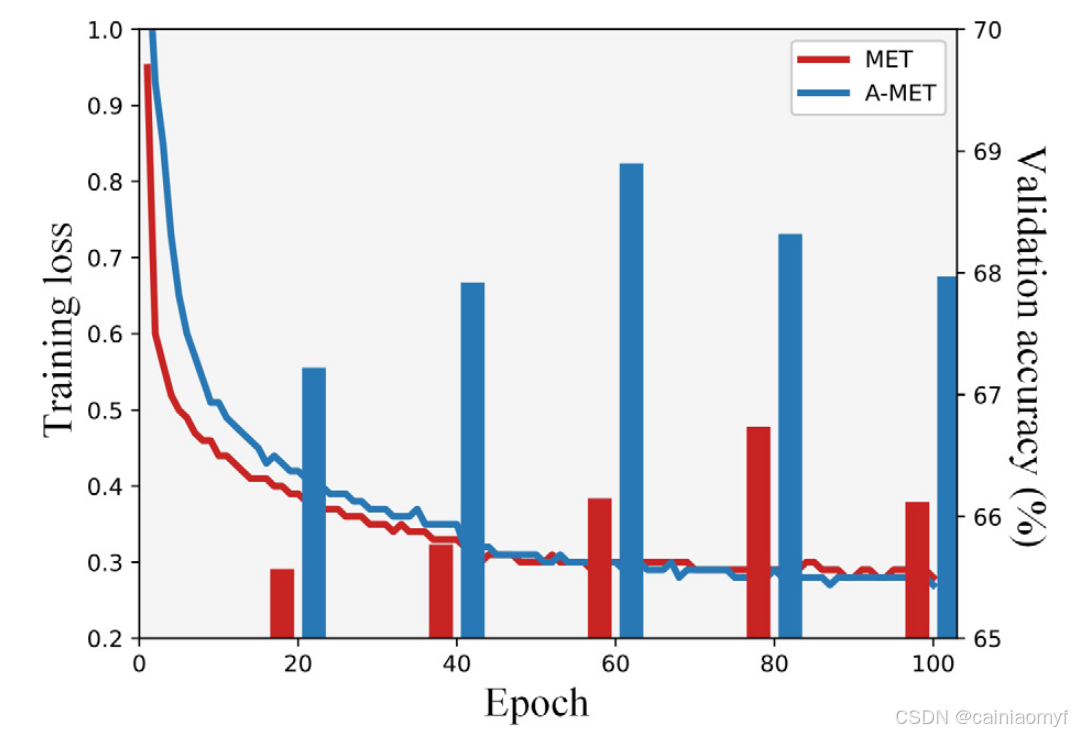
预训练和元训练阶段都以情境方式进行评估,并且采样策略与元训练一致。具体来说,验证间隔为 20 轮,每个验证阶段包括 600 个情境。为了进行公平比较,我们根据验证集进行模型选择。mini-ImageNet 的训练损失曲线和验证结果如图 6 所示。我们可以观察到,A-MET 在 60 轮时的验证准确性比 MET 更高。这表明 A-MET 能够更有效地从有限的标记数据中学习。在测试阶段,我们执行 2000 个情境,并重复该过程 5 次以获取平均准确率。我们报告所有实验的平均准确率和相应的 95% 置信区间。
图6 所提出的 A-MET 范式与基线范式 MET 的训练损失曲线和验证结果。训练在 mini-ImageNet 数据集上使用 ResNet-12 架构进行
实验环境
实验在 Ubuntu 16.04 和 1 个 NVIDIA RTX 3090 GPU 上进行。实现基于 PyTorch 1.8 和 Python 3.7。对于 Omniglot 和 mini-ImageNet,预训练阶段占用约 5 GB 的 GPU 内存。对于 tiered-ImageNet,预训练阶段占用约 11 GB 的 GPU 内存。在元训练阶段,上述数据集均占用约 5 GB 的 GPU 内存。
4.5. Main results
我们将所提出的方法与经典的以及最新的小样本学习(FSC)任务中的工作进行了比较。Matching Networks 1 在实验中使用了非标准的训练/测试划分,ProtoNet 28 并未在 ResNet-12 上进行实验,因此我们使用了之前工作 1942 的重新实现结果。需要注意的是,比较方法引入了更多精心设计的架构,而我们的方法在没有任何额外模块的简单网络下实现了具有竞争力甚至更好的性能。
在接下来的实验中,我们将“Linear”表示为迁移学习策略,将“MET”(Meta-Transfer)表示为之前的两阶段学习范式,将“A-MET”(Adaptive Meta-Transfer)表示为我们提出的学习范式。
5-way 1-shot 和 5-way 5-shot 分类任务的比较结果。平均准确率(%)带有 95% 置信区间。最佳结果以 \textbf{粗体黑字} 表示,红色字体表示基于基线 MET 的改进 1 15 19 21 22 23 28 33 34 35 42 43 44
| Method | Backbone | mini-ImageNet 1-shot | mini-ImageNet 5-shot | tiered-ImageNet 1-shot | tiered-ImageNet 5-shot |
|---|---|---|---|---|---|
| Matching Networks 1 | ConvNet-4 | 43.56 ± 0.84 | 55.31 ± 0.73 | - | - |
| MAML 15 | ConvNet-4 | 48.70 ± 1.84 | 63.11 ± 0.92 | 51.67 ± 1.81 | 70.30 ± 1.75 |
| ProtoNet 28 | ConvNet-4 | 49.42 ± 0.78 | 68.20 ± 0.66 | 54.48 ± 0.93 | 71.32 ± 0.78 |
| RelationNet 22 | ConvNet-4 | 50.44 ± 0.82 | 65.32 ± 0.70 | 51.68 ± 0.50 | 70.30 ± 0.36 |
| Linear | ConvNet-4 | 50.44 ± 0.47 | 65.37 ± 0.37 | - | - |
| MET | ConvNet-4 | 51.16 ± 0.46 | 66.64 ± 0.37 | 51.81 ± 0.49 | 70.21 ± 0.36 |
| A-MET (Ours) | ConvNet-4 | 54.10 ± 0.47 (+2.94) | 68.77 ± 0.38 (+2.13) | 54.92 ± 0.52 (+3.11) | 71.77 ± 0.42 (+1.56) |
| A-MET w/ GSCM (Ours) | ConvNet-4 | 56.64 ± 0.51 (+5.48) | 69.88 ± 0.38 (+3.24) | 59.65 ± 0.54 (+7.84) | 72.67 ± 0.43 (+2.46) |
| Matching Networks 1 | ResNet-12 | 63.08 ± 0.80 | 75.99 ± 0.60 | 68.50 ± 0.92 | 80.60 ± 0.71 |
| ProtoNet 28 | ResNet-12 | 60.37 ± 0.83 | 78.02 ± 0.57 | 61.74 ± 0.77 | 80.00 ± 0.55 |
| CANet 23 | ResNet-12 | 63.85 ± 0.48 | 79.44 ± 0.34 | 69.89 ± 0.51 | 84.23 ± 0.37 |
| ProtoNets+TRAML 43 | ResNet-12 | 60.31 ± 0.84 | 77.94 ± 0.57 | - | - |
| Meta-Baseline 19 | ResNet-12 | 63.17 ± 0.23 | 79.26 ± 0.17 | 68.62 ± 0.27 | 83.74 ± 0.18 |
| ConstellationNet 44 | ResNet-12 | 64.69 ± 0.42 | 79.95 ± 0.17 | 71.61 ± 0.51 | 85.28 ± 0.35 |
| RENet 35 | ResNet-12 | 67.60 ± 0.44 | 83.25 ± 0.31 | 65.99 ± 0.72 | 81.56 ± 0.53 |
| MetaOptNet 33 | ResNet-12 | 62.64 ± 0.61 | 78.63 ± 0.46 | 66.10 ± 0.52 | 81.34 ± 0.61 |
| MetaOptNet+ArL 34 | ResNet-12 | 65.21 ± 0.58 | 81.41 ± 0.49 | - | - |
| APP2S 42 | ResNet-12 | 66.25 ± 0.20 | 83.42 ± 0.15 | 72.00 ± 0.22 | 86.23 ± 0.15 |
| DeepBDC 21 | ResNet-12 | 67.34 ± 0.43 | 84.46 ± 0.28 | 72.34 ± 0.49 | 87.31 ± 0.32 |
| Linear | ResNet-12 | 62.07 ± 0.46 | 78.90 ± 0.33 | 65.76 ± 0.55 | 79.15 ± 0.41 |
| MET | ResNet-12 | 63.16 ± 0.47 | 78.86 ± 0.33 | 66.25 ± 0.54 | 79.30 ± 0.40 |
| A-MET (Ours) | ResNet-12 | 64.61 ± 0.47 (+1.45) | 80.06 ± 0.32 (+1.20) | 69.39 ± 0.57 (+3.14) | 81.11 ± 0.39 (+1.81) |
| A-MET w/ GSCM (Ours) | ResNet-12 | 68.47 ± 0.51 (+5.31) | 80.89 ± 0.33 (+2.03) | 74.08 ± 0.54 (+7.83) | 84.91 ± 0.35 (+5.61) |
基于 ImageNet 基准的结果
表 1 展示了在两个基于 ImageNet 的数据集上的比较结果,这些数据集具有不同程度的领域重叠,使用了两种不同的特征编码器结构。显然,MET 在这两个数据集上的改进有限,甚至在 tiered-ImageNet 上表现出负面效果。这一发现强调了由不同学习目标引起的实例特定偏差对编码器的影响。因此,通过消除这种偏差并使编码器的学习目标朝向一般特征,A-MET 显示出显著的改进。此外,我们观察到,所提出的方法在这两种常见架构上始终提高了模型性能。通常,A-MET 在 tiered-ImageNet 上的改进更为显著。这一现象支持了我们的分析,即 MET 更容易受到不期望的不完整特征的影响,这限制了模型向新类推广的可迁移性。我们还注意到,GSCM 对平均准确率总是有帮助,并且在具有挑战性的 1-shot 设置下具有更多优势。这表明当可用的支持样本较少时,GSCM 有助于区分共性。总体而言,在 tiered-ImageNet 上的改进大于 mini-ImageNet 上的改进。这证明了所提出的方法在基类和新类之间存在较大领域差异的场景中受益更多。与其他方法相比,所提出的方法在没有额外模块的简单网络下获得了相当或更好的性能。
表2 5-way 和 20-way 1-shot 分类任务在Omniglot 上的比较结果。所有方法的特征编码器为 convnet-4。常见且难以表示数据拆分设置。
| Setting | Method | 5-way | 20-way |
|---|---|---|---|
| Common | Matching Networks [1] ProtoNet [28] RENet [35] MET A-MET w/ GSCM (Ours) | 97.90 98.80 99.32 98.50 99.50 | 93.50 96.00 96.73 96.00 98.53 |
| Hard | Matching Networks [1] ProtoNet [28] RENet [35] MET A-MET w/ GSCM (Ours) | 97.44 97.95 98.18 98.31 98.74 | 93.91 94.46 95.70 95.31 96.12 |
Omniglot 上的结果
Omniglot 的比较结果如表 2 所示。我们首先在 Vinyals 等人 1 提出的常见数据设置(“Common”)上评估了模型。这是一个较简单的设置,所有工作在 5-way 1-shot 任务上都取得了很高的准确率。此外,我们在更具挑战性的设置(“Hard”)40 下评估了模型。在这种设置下,所提出的方法相比于其他方法获得了更好的结果。这表明,所提出的方法在基类和新类之间存在较大领域差异的场景中具有更多优势。
| Method | mini-ImageNet → Omniglot 5-w 1-s | mini-ImageNet → Omniglot 5-w 5-s | mini-ImageNet → Omniglot 20-w 1-s | mini-ImageNet → Omniglot 20-w 5-s | mini-ImageNet → CUB 5-w 1-s | mini-ImageNet → CUB 5-w 5-s | mini-ImageNet → CUB 20-w 1-s | mini-ImageNet → CUB 20-w 5-s |
|---|---|---|---|---|---|---|---|---|
| MET (Ours) | 76.16 | 90.36 | 52.36 | 75.35 | 45.41 | 62.01 | 14.69 | 23.91 |
| A-MET (Ours) | 81.84 | 93.29 | 60.94 | 82.12 | 47.28 | 64.64 | 18.48 | 28.21 |
| A-MET w/ GSCM (Ours) | 86.89 | 94.17 | 64.52 | 83.35 | 49.46 | 64.95 | 22.01 | 31.43 |
跨领域评估
我们在两个设置下对所提出方法的跨领域迁移能力进行了进一步评估:(i)从通用物体数据集 mini-ImageNet 到手写字符数据集 Omniglot,及(ii)从通用物体数据集 mini-ImageNet 到细粒度数据集 CUB。具体来说,模型在 mini-ImageNet 的训练集上进行训练,该训练集包含 64 个类别并遵循标准设置。对于 Omniglot 数据集,我们采用了基于字母表级别的具有挑战性的数据划分,用于跨领域评估的测试集包含 20 个字母表。对于 CUB,我们使用整个数据集进行评估,该数据集包含 200 个类别。评估结果分别如表 3 和表 4 所示。从表中可以观察到,A-MET 有效地促进了模型的可迁移性。对于 Omniglot,在 1-shot 设置下,无论是 5-way 还是 20-way 设置,改进幅度都大于 5-shot 设置。对于更具挑战性的 CUB,总体改进幅度小于 Omniglot。可能的原因是细粒度分类任务需要更多对细节的关注,而 A-MET 更加关注一般特征。结果还支持我们的分析,即 MET 容易产生不期望的表示,而所提出的方法在具有挑战性的设置下更为有效。此外,GSCM 在 1-shot 上取得了更多进展,这证明了为样本提供合适的嵌入总是有帮助的。
表 5 模型在小样本数条件下泛化能力的鲁棒性定量结果
| shots | MET | A-MET | A-MET w/ GSCM |
|---|---|---|---|
| 5 | 78.37 ± 0.34 | 80.20 ± 0.32 | 80.82 ± 0.33 |
| 4 | 77.18 ± 0.35 | 78.70 ± 0.34 | 79.55 ± 0.35 |
| 3 | 74.88 ± 0.37 | 76.53 ± 0.36 | 77.83 ± 0.37 |
| 2 | 71.05 ± 0.41 | 72.70 ± 0.40 | 74.75 ± 0.42 |
| 1 | 63.13 ± 0.46 | 64.61 ± 0.47 | 68.47 ± 0.51 |
表 6 模型在大类别数条件下泛化能力的鲁棒性定量结果
| ways | MET | A-MET | A-MET w/ GSCM |
|---|---|---|---|
| 5 | 63.16 ± 0.47 | 64.41 ± 0.47 | 68.47 ± 0.51 |
| 6 | 59.00 ± 0.41 | 60.36 ± 0.42 | 64.16 ± 0.46 |
| 7 | 55.16 ± 0.38 | 56.72 ± 0.38 | 60.71 ± 0.41 |
| 8 | 52.11 ± 0.34 | 53.86 ± 0.35 | 57.20 ± 0.38 |
| 9 | 47.16 ± 0.31 | 51.07 ± 0.31 | 54.76 ± 0.30 |
| 10 | 42.99 ± 0.26 | 48.85 ± 0.29 | 52.31 ± 0.33 |
鲁棒性分析
表 5、表 6 和图 7 展示了定量和图形化的结果,证明了模型在推广到更少的 shots 或更多的 ways 上的鲁棒性。首先,我们测试了在 5-way 5-shot 任务上训练的模型在更小的 K-shot 设置(
K
<
5
K < 5
K<5)下的表现。我们可以观察到,当 2-shot → 1-shot 时,模型的性能急剧下降。直观上,可能的原因是 1-shot 设置存在更大的不确定性,否则这种不确定性会减小。此外,我们还测试了在 5-way 1-shot 任务上训练的模型在更大的 C-way 设置(
C
>
5
C > 5
C>5)下的表现。我们可以观察到,A-MET 在逐渐增加的 C-way 设置中显示出优势。两条曲线均显示 GSCM 有利于 1-shot 情况,而 A-MET 通过学习通用特征表示提高了整体性能。
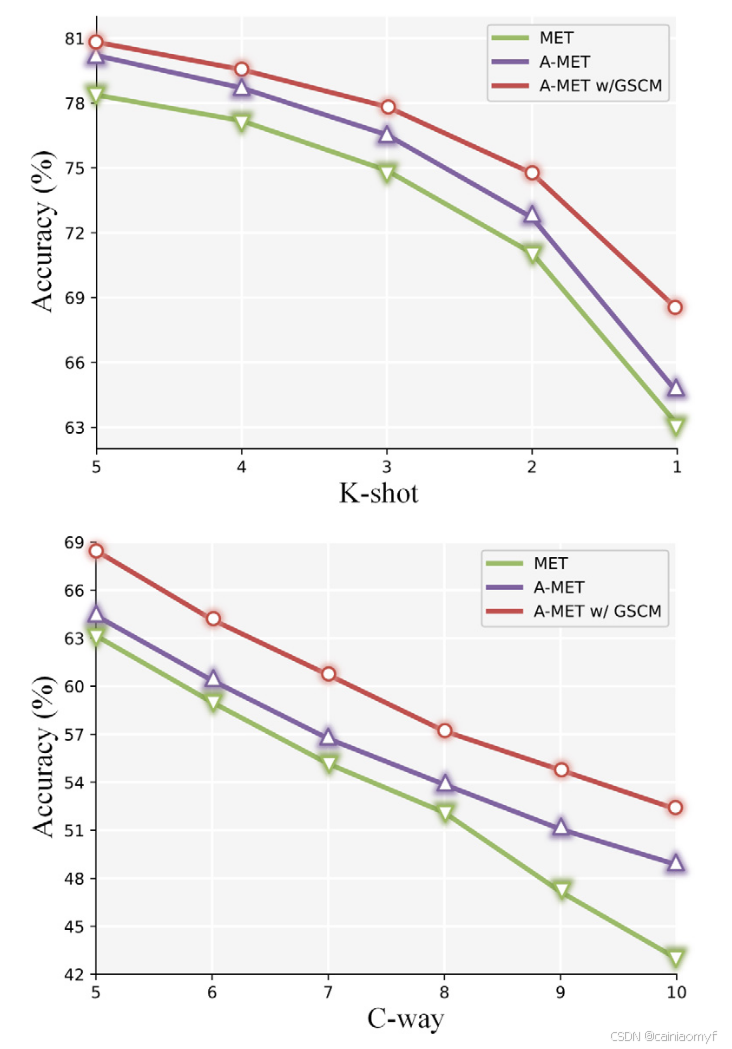
表 7 mini-imagenet 的平均 5 路准确度。基础代。和新颖的一代。分别表示基类和新类的泛化能力
| Method | Base gen. 1-shot | Base gen. 5-shot | Novel gen. 1-shot | Novel gen. 5-shot |
|---|---|---|---|---|
| MET | 87.26 | 93.53 | 65.07 | 80.26 |
| A-MET | 87.37 | 93.29 | 69.76 | 81.98 |
4.6. Ablation analysis
我们进行了消融分析以验证所提出方法中每个组件的有效性。消融研究分别在 mini- 和 tiered-ImageNet 上针对 5-way 1-shot 和 5-shot 任务进行。我们使用 ResNet-12 作为特征提取器。消融研究的结果如表 8、表 7、图 8 和图 9 所示。表 8 的第一行代表预训练阶段。从表 8 中可以看到,所提出方法的平均改进为 5.62%。
| MET | ADAPTIVE | GSCM | mini-ImageNet 1-shot | Δ | mini-ImageNet 5-shot | Δ | tiered-ImageNet 1-shot | Δ | tiered-ImageNet 5-shot | Δ |
|---|---|---|---|---|---|---|---|---|---|---|
| ✓ | 62.07 | – | 78.90 | – | 65.76 | – | 79.15 | – | ||
| ✓ | ✓ | 63.16 | +1.09 | 78.86 | −0.04 | 66.25 | +0.49 | 79.30 | +0.15 | |
| ✓ | ✓ | 64.61 | +2.54 | 80.06 | +1.16 | 69.39 | +3.63 | 81.11 | +1.96 | |
| ✓ | ✓ | ✓ | 66.75 | +4.68 | 79.08 | +0.18 | 72.81 | +7.05 | 80.13 | +0.98 |
| ✓ | ✓ | ✓ | 68.47 | +6.40 | 80.89 | +1.99 | 74.08 | +8.32 | 84.91 | +5.76 |
A-MET 的效果
表 8 显示了 mini- 和 tiered-ImageNet 上的预测结果。如前所述,mini-ImageNet 具有较大的领域重叠,因为它没有考虑基类和新类之间的相似性,而 tiered-ImageNet 则相反。我们可以观察到,所提出的 A-MET 范式在这两种情况下都有效,并且在 tiered-ImageNet 数据集上表现更好。这表明 A-MET 能够消除实例特定偏差,并增强模型向新类迁移的能力。结果还突出了 A-MET 在适应具有不同领域重叠的数据集中的重要性。
图8 查询样本的类激活映射(CAM)可视化结果。Linear 代表通过标准监督方式预训练的特征编码器
图 8 展示了三种不同方法的查询样本的可视化类激活图(CAM)。我们观察到,通过标准监督方法预训练的特征编码器倾向于关注小而不完整的特征(“Linear”)。尽管通过元学习策略对编码器进行了微调以适应小样本任务,但仍有一些特征不适合两个样本之间的相似性度量(“MET”)。这种现象可能导致下游任务或操作中的次优性能。相比之下,通过所提出的 A-MET 范式训练的模型能够捕捉到更通用和更鲁棒的特征。可视化的 CAM 结果证明了 A-MET 在学习可推广且对下游任务更具鲁棒性的特征表示中的有效性。
图9 基于不同支持样本的查询样本类激活映射(CAM)。结果表明,查询样本的预测应参考支持样本,以获得更一致的焦点区域。注意,CAM 是通过所提出的方法得到的
表 7 展示了模型对基类和新类的泛化能力。基类的泛化性能通过从基类中的未见样本中采样情境进行评估,而新类的泛化性能是指从新类中采样的情境的表现。具体来说,我们将基类定义为训练集,未见样本从未包含在 mini-ImageNet 中的 ILSVRC-2012 数据集中选取。对于新类,我们使用验证集和测试集的组合,总共包含 36 个类别。从表中可以看出,与 MET 相比,使用 A-MET 训练的模型在新类上获得了更高的泛化性能,同时在基类上保持了具有竞争力的表现。
GSCM 的效果
定量结果如表 8 所示。我们可以看到,GSCM 在评估指标上有显著的提升。与 MET 相比,它将平均准确率提高了 3.22%。得益于 GSCM,查询样本的预测可以参考情境中的相应支持样本,从而获得更一致的预测结果。与 1-shot 相比,GSCM 在 5-shot 设置下的改进有限。这可以归因于 5-shot 设置提供了更多的支持信息,从而减少了无关特征对预测结果的影响。
图 9 显示了具有不同支持样本的查询样本的焦点区域的可视化结果。可视化结果表明,查询样本的焦点区域与相应的支持样本更一致,这验证了 GSCM 在减少无关特征对模型预测影响中的有效性。
5. Conclusion
在本文中,我们提出了一种能够有效执行小样本分类任务的简单方法。首先,我们基于小样本分类(FSC)任务,探讨了迁移学习与元学习策略之间协作的深入见解。我们的实验揭示了这两种学习策略之间被忽视的差异。其次,我们为 FSC 任务提出了一种新的学习范式,旨在在元训练阶段分离不期望的表示。此外,我们分析了预测机制,并提出了一种新的度量方法,以实现更一致的预测。最后,我们在四个公共 FSC 基准上评估了所提出的方法。实验结果表明,所提出的方法在常见设置中能够持续提升性能,并在新类上实现更好的泛化性。所提出的方法与特定网络结构解耦,能够应用于任意架构。同时,所提出的方法在基类和新类之间存在较大领域差异以及支持信息较少的情况下更具优势。
尽管表现出色,所提出的 A-MET 范式确实存在一定的局限性。它专为两阶段的小样本学习策略设计,因为对抗训练的关键分类器来自于第一阶段。此外,GSCM 的有效性在某种程度上依赖于特征嵌入。与直接在 MET 上应用 GSCM 相比,A-MET 能够通过确保鲁棒的特征嵌入进一步展示其能力。解决这些局限性的潜在解决方案是设计一个能够自发消除偏差的去偏置网络。这可以通过将一个偏差指示器集成到网络中并进行端到端的训练来实现。这种方法与文献 45 中提出的工作类似,并已显示出可行性。在未来的工作中,我们计划研究一种将所提出方法的优势整合的端到端小样本学习任务解决方案。此外,我们还计划探索该方法在各种其他小样本学习任务中的适用性。
O. Vinyals, C. Blundell, T. Lillicrap, D. Wierstra, et al., Matching networks for one shot learning, in: Advances in Neural Information Processing Systems, Vol. 29, 2016, http://dx.doi.org/10.48550/arXiv.1606.04080. ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎
L. Zhang, S. Zhang, B. Zou, H. Dong, Unsupervised deep representation learning and few-shot classification of PolSAR images, IEEE Trans. Geosci. Remote Sens. 60 (2020) 1–16, http://dx.doi.org/10.1109/TGRS.2020.3043191. ↩︎
X. Li, J. Deng, Y. Fang, Few-shot object detection on remote sensing images, IEEE Trans. Geosci. Remote Sens. 60 (2021) 1–14, http://dx.doi.org/10.1109/TGRS.2021.3051383. ↩︎
L. Lai, J. Chen, C. Zhang, Z. Zhang, G. Lin, Q. Wu, Tackling background ambiguities in multi-class few-shot point cloud semantic segmentation, Knowl.-Based Syst. 253 (2022) 109508, http://dx.doi.org/10.1016/j.knosys.2022.109508. ↩︎
G.S. Dhillon, P. Chaudhari, A. Ravichandran, S. Soatto, A baseline for few-shot image classification, 2019, http://dx.doi.org/10.48550/arXiv.1909.02729, arXiv preprint arXiv:1909.02729. ↩︎ ↩︎
W.-Y. Chen, Y.-C. Liu, Z. Kira, Y.-C.F. Wang, J.-B. Huang, A closer look at few-shot classification, 2019, http://dx.doi.org/10.48550/arXiv.1904.04232, arXiv preprint arXiv:1904.04232. ↩︎ ↩︎ ↩︎ ↩︎
Y. Tian, Y. Wang, D. Krishnan, J.B. Tenenbaum, P. Isola, Rethinking few-shot image classification: a good embedding is all you need? in: European Conference on Computer Vision, Springer, 2020, pp. 266–282, http://dx.doi.org/10.1007/978-3-030-58568-6_16. ↩︎ ↩︎
S. Qiao, C. Liu, W. Shen, A.L. Yuille, Few-shot image recognition by predicting parameters from activations, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 7229–7238, http://dx.doi.org/10.48550/arXiv.1706.03466. ↩︎ ↩︎
A.A. Rusu, D. Rao, J. Sygnowski, O. Vinyals, R. Pascanu, S. Osindero, R. Hadsell, Meta-learning with latent embedding optimization, in: International Conference on Learning Representations, 2018, http://dx.doi.org/10.48550/arXiv.1807.05960. ↩︎ ↩︎ ↩︎
T. Scott, K. Ridgeway, M.C. Mozer, Adapted deep embeddings: A synthesis of methods for k-shot inductive transfer learning, Adv. Neural Inf. Process. Syst. 31 (2018) https://dl.acm.org/doi/abs/10.5555/3326943.3326951. ↩︎ ↩︎
A. Nakamura, T. Harada, Revisiting fine-tuning for few-shot learning, 2019, http://dx.doi.org/10.48550/arXiv.1910.00216, arXiv preprint arXiv:1910.00216. ↩︎
A. Kolesnikov, L. Beyer, X. Zhai, J. Puigcerver, J. Yung, S. Gelly, N. Houlsby, Big transfer (bit): General visual representation learning, in: European Conference on Computer Vision, Springer, 2020, pp. 491–507, http://dx.doi.org/10.1007/978-3-030-58558-7_29. ↩︎
J. Deng, W. Dong, R. Socher, L.-J. Li, K. Li, L. Fei-Fei, Imagenet: A large-scale hierarchical image database, in: 2009 IEEE Conference on Computer Vision and Pattern Recognition, Ieee, 2009, pp. 248–255, http://dx.doi.org/10.1109/CVPR.2009.5206848. ↩︎
D.K. Naik, R.J. Mammone, Meta-neural networks that learn by learning, in: [Proceedings 1992] IJCNN International Joint Conference on Neural Networks, Vol. 1, IEEE, 1992, pp. 437–442, http://dx.doi.org/10.1109/IJCNN.1992.287172. ↩︎
C. Finn, P. Abbeel, S. Levine, Model-agnostic meta-learning for fast adaptation of deep networks, in: International Conference on Machine Learning, PMLR, 2017, pp. 1126–1135, https://dl.acm.org/doi/abs/10.5555/3305381.3305498. ↩︎ ↩︎ ↩︎
S. Gidaris, N. Komodakis, Dynamic few-shot visual learning without forgetting, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 4367–4375, https://doi.ieeecomputersociety.org/10.1109/CVPR.2018.00459. ↩︎
Q. Sun, Y. Liu, T.-S. Chua, B. Schiele, Meta-transfer learning for few-shot learning, in: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2019, pp. 403–412, http://dx.doi.org/10.1109/CVPR.2019.00049. ↩︎ ↩︎
C. Zhang, Y. Cai, G. Lin, C. Shen, Deepemd: Few-shot image classification with differentiable earth mover’s distance and structured classifiers, in: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2020, pp. 12203–12213, http://dx.doi.org/10.1109/CVPR42600.2020.01222. ↩︎
Y. Chen, Z. Liu, H. Xu, T. Darrell, X. Wang, Meta-baseline: Exploring simple meta-learning for few-shot learning, in: Proceedings of the IEEE/CVF International Conference on Computer Vision, 2021, pp. 9062–9071, http://dx.doi.org/10.1109/ICCV48922.2021.00893. ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎
D. Wertheimer, L. Tang, B. Hariharan, Few-shot classification with feature map reconstruction networks, in: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2021, pp. 8012–8021, http://dx.doi.org/10.1109/CVPR46437.2021.00792. ↩︎ ↩︎
J. Xie, F. Long, J. Lv, Q. Wang, P. Li, Joint distribution matters: Deep brownian distance covariance for few-shot classification, in: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2022, pp. 7972–7981, http://dx.doi.org/10.1109/CVPR52688.2022.00781. ↩︎ ↩︎ ↩︎
F. Sung, Y. Yang, L. Zhang, T. Xiang, P.H. Torr, T.M. Hospedales, Learning to compare: Relation network for few-shot learning, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 1199–1208, http://dx.doi.org/10.1109/CVPR.2018.00131. ↩︎ ↩︎ ↩︎ ↩︎ ↩︎
R. Hou, H. Chang, B. Ma, S. Shan, X. Chen, Cross attention network for few-shot classification, Adv. Neural Inf. Process. Syst. 32 (2019) http://dx.doi.org/10.48550/arXiv.1910.07677. ↩︎ ↩︎ ↩︎ ↩︎ ↩︎
M. Ren, E. Triantafillou, S. Ravi, J. Snell, K. Swersky, J.B. Tenenbaum, H. Larochelle, R.S. Zemel, Meta-learning for semi-supervised few-shot classification, 2018, http://dx.doi.org/10.48550/arXiv.1803.00676, arXiv preprint arXiv:1803.00676. ↩︎ ↩︎ ↩︎
B.M. Lake, R. Salakhutdinov, J.B. Tenenbaum, Human-level concept learning through probabilistic program induction, Science 350 (6266) (2015) 1332–1338, http://dx.doi.org/10.1126/science.aab3050. ↩︎ ↩︎ ↩︎ ↩︎
C. Wah, S. Branson, P. Welinder, P. Perona, S. Belongie, The caltech-ucsd birds-200-2011 dataset, 2011, https://authors.library.caltech.edu/27452/. ↩︎ ↩︎ ↩︎
S.J. Pan, Q. Yang, A survey on transfer learning, IEEE Trans. Knowl. Data Eng. 22 (10) (2009) 1345–1359, http://dx.doi.org/10.1109/TKDE.2009.191. ↩︎
J. Snell, K. Swersky, R. Zemel, Prototypical networks for few-shot learning, in: Advances in Neural Information Processing Systems, Vol. 30, 2017, https://dl.acm.org/doi/abs/10.5555/3294996.3295163. ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎
A. Santoro, S. Bartunov, M. Botvinick, D. Wierstra, T. Lillicrap, Meta-learning with memory-augmented neural networks, in: International Conference on Machine Learning, PMLR, 2016, pp. 1842–1850, https://proceedings.mlr.press/v48/santoro16.html. ↩︎
N. Mishra, M. Rohaninejad, X. Chen, P. Abbeel, A simple neural attentive meta-learner, in: International Conference on Learning Representations, 2018, http://dx.doi.org/10.48550/arXiv.1707.03141. ↩︎
T. Munkhdalai, X. Yuan, S. Mehri, A. Trischler, Rapid adaptation with conditionally shifted neurons, in: International Conference on Machine Learning, PMLR, 2018, pp. 3664–3673, http://dx.doi.org/10.48550/arXiv.1712.09926. ↩︎
E. Grant, C. Finn, S. Levine, T. Darrell, T. Griffiths, Recasting gradient-based meta-learning as hierarchical bayes, in: International Conference on Learning Representations, 2018, http://dx.doi.org/10.48550/arXiv.1801.08930. ↩︎
K. Lee, S. Maji, A. Ravichandran, S. Soatto, Meta-learning with differentiable convex optimization, in: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2019, pp. 10657–10665, http://dx.doi.org/10.1109/CVPR.2019.01091. ↩︎ ↩︎ ↩︎
H. Zhang, P. Koniusz, S. Jian, H. Li, P.H. Torr, Rethinking class relations: Absolute-relative supervised and unsupervised few-shot learning, in: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2021, pp. 9432–9441, http://dx.doi.org/10.48550/arXiv.2001.03919. ↩︎ ↩︎ ↩︎ ↩︎
D. Kang, H. Kwon, J. Min, M. Cho, Relational embedding for few-shot classification, in: Proceedings of the IEEE/CVF International Conference on Computer Vision, 2021, pp. 8822–8833, http://dx.doi.org/10.1109/ICCV48922.2021.00870. ↩︎ ↩︎ ↩︎
Z. Yue, H. Zhang, Q. Sun, X.-S. Hua, Interventional few-shot learning, in: Advances in Neural Information Processing Systems, Vol. 33, 2020, pp. 2734–2746, https://dl.acm.org/doi/abs/10.5555/3495724.3495954. ↩︎
X. Chen, M. Ding, X. Wang, Y. Xin, S. Mo, Y. Wang, S. Han, P. Luo, G. Zeng, J. Wang, Context autoencoder for self-supervised representation learning, 2022, http://dx.doi.org/10.48550/arXiv.2202.03026, arXiv preprint arXiv:2202.03026. ↩︎
B. Kim, H. Kim, K. Kim, S. Kim, J. Kim, Learning not to learn: Training deep neural networks with biased data, in: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2019, pp. 9012–9020, http://dx.doi.org/10.48550/arXiv.1812.10352. ↩︎
O. Russakovsky, J. Deng, H. Su, J. Krause, S. Satheesh, S. Ma, Z. Huang, A. Karpathy, A. Khosla, M. Bernstein, et al., Imagenet large scale visual recognition challenge, Int. J. Comput. Vis. 115 (3) (2015) 211–252, http://dx.doi.org/10.1007/s11263-015-0816-y. ↩︎ ↩︎
E. Triantafillou, T. Zhu, V. Dumoulin, P. Lamblin, U. Evci, K. Xu, R. Goroshin, C. Gelada, K. Swersky, P.-A. Manzagol, et al., Meta-dataset: A dataset of datasets for learning to learn from few examples, 2019, http://dx.doi.org/10.48550/arXiv.1903.03096, arXiv preprint arXiv:1903.03096. ↩︎ ↩︎
S. Ravi, H. Larochelle, Optimization as a model for few-shot learning, 2016, https://openreview.net/forum?id=rJY0-Kcll. ↩︎ ↩︎
R. Ma, P. Fang, T. Drummond, M. Harandi, Adaptive Poincaré point to set distance for few-shot classification, in: Proceedings of the AAAI Conference on Artificial Intelligence, 2022, pp. 1926–1934, http://dx.doi.org/10.1609/aaai.v36i2.20087. ↩︎ ↩︎ ↩︎
A. Li, W. Huang, X. Lan, J. Feng, Z. Li, L. Wang, Boosting few-shot learning with adaptive margin loss, in: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2020, pp. 12576–12584, http://dx.doi.org/10.1109/CVPR42600.2020.01259. ↩︎ ↩︎
W. Xu, Y. Xu, H. Wang, Z. Tu, Attentional constellation nets for few-shot learning, in: International Conference on Learning Representations, 2021, https://openreview.net/forum?id=vujTf_I8Kmc. ↩︎ ↩︎
S. Qu, Y. Pan, G. Chen, T. Yao, C. Jiang, T. Mei, Modality-agnostic debiasing for single domain generalization, in: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2023, pp. 24142–24151, http://dx.doi.org/10.48550/arXiv.2303.07123. ↩︎