摘要
对于室内复杂环境来说, 适用于室外定位的 GPS 系统和蜂窝移动网络在室内中的定位精度明显恶化, 无法满足室内用户精确定位的需求。因此, 研究一种适用于室内复杂环境的高精度、环境自适应性强的定位算法成为近年来该领域的热点。本文用真实环境下的信号强度衰减数据作为模型进行对数衰减模型的构建,将原有基于 RSS 数据库位置的模型转换为 RSS数据库距离数据库位置的指纹定位模型,增加模型的可移植性与运行效率。
引言
随着智能穿戴等嵌入式设备和移动通信技术的发展,LSB1被广泛关注。LBS的核心技术是定位。目前,GPS和北斗定位系统(BeiDou Navigation Satellite System)是最广为人知的定位系统,这些系统在户外定位方面表现非常好。然而,由于许多原因(主要是卫星与接收器之间存在障碍物),它在城市峡谷中不可靠,在室内几乎不可用。实际上,电磁波受到建筑物和森林、山体等外部障碍物的影响。2另外,在无线传感器网络的每个节点上使用GPS和北斗的成本也很高,许多领域甚至会舍弃精确度而采用其他定位方法。为了获得建筑物内部的精确位置,人们探索了许多邻近技术。
由于室内环境十分复杂,信号多径干扰严重、参考时钟精确性不高等问题,基于测距的方法在室内定位中误差较大。相比基于信号时间和角度的定位方法,基于RSSI3位置指纹的定位方法通常无需添加额外的硬件,具有检测设备成本低,测量信号稳定性好,定位方法简单等优点。“位 置指纹“是把室内环境中的位置和该位置的某些特定信号强度关联起来,一个位置对应唯一的指纹。 这样就能通过模式匹配的方式完成室内定位。位置指纹定位主要分为两个阶段,一是离线阶段,离线阶段主要是信息采集和样本训练,利用参考点的已知位置数据和接收到的接入点的RSSI信号特征值(RSSI、MAC地址、最值、均值、方差、方向、概率等)建立位置一指纹数据库,从而建立空间位置与RSSI序列的映射关系;二是在线阶段,将待定位节点与信号位置指纹数据库进行匹配,从而实现节点定位,因其实现简单,定位成本较低,所以成为室内定位的主要算法71。近几年来常见的用于指纹匹配定位的机器学习方法有: K最近邻法、支持向量机、随机森林、卷积神经网络、循环神经网络等,本节将主要介绍以上五种方法在室内定位中的应用4。
“位置指纹”把实际环境中的位置和某种“指纹”联系起来,一个位置对应一个独特的指纹。这个指纹可以是单维或多维的,比如待定位设备在接收或者发送信息,那么指纹可以是这个信息或信号的一个特征或多个特征(最常见的是信号强度)。如果待定位设备是在发送信号,由一些固定的接收设备感知待定位设备的信号或信息然后给它定位,这种方式常常叫做\textbf{远程定位或者网络定位}。如果是待定位设备接收一些固定的发送设备的信号或信息,然后根据这些检测到的特征来估计自身的位置,这种方式可称为\textbf{自身定位}。以上两者的有机结合称为\textbf{混合定位}:待定位移动设会把它检测到的特征传达给网络中的服务器节点,服务器可以利用它所能获得的所有信息来估计移动设备的位置。在所有的这些方式中,都需要把感知到的信号特征拿去匹配一个数据库中的信号特征,这个过程可以看作一个模式识别的问题,是机器学习类的经典问题。
位置指纹可以是多种类型的,任何“位置独特”的(对区分位置有帮助的)特征都能被用来做为一个位置指纹。比如某个位置上通信信号的多径结构、某个位置上是否能检测到接入点或基站、某个位置上检测到的来自基站信号的RSS5、某个位置上通信时信号的往返时间或延迟,这些都能作为一个位置指纹,或者也可以将其组合起来作为位置指纹6。
目前许多学者在进行指纹定位时,多运用基站RSS作为位置指纹,因为RSS的值容易获取,但是因为每个基站信号衰减模型不可能完全相等、同一基站不同时间下的信号衰减模型也不一定相等,如果遇到基站故障、发射功率变更等情况,所有指纹点均需要重新训练,后期维护成本过高。
本文基于此项现状,提出了RSS-距离-位置的指纹定位模型,用于训练的数据库不再是多个RSS的数据,而是经换算后的距离数据,在基站的功率发生变化时,仅需要以很少的样本测试得到RSS的距离衰减函数,则可以运用原有的模型进行指纹定位,进而确定位置信息。节省了模型的后期维护成本,同时提高模型的可移植性,即使更换了所有的发射基站,原有模型在经过简单的计算后依然可以直接使用。
理论介绍
指纹
位置指纹可以是多种类型的,任何“位置独特”的(对区分位置有帮助的)特征都能被用来做为一个位置指纹。
在某个恒定的发射功率下,信号的RSS取决于接收器的位置。RSS的获取很简单,因为它是大多数无线通信设备正常运行中所必需的。很多通信系统需要RSS信息用来感知链路的质量,实现切换,适应传输速率等功能。RSS不受信号带宽的影响,不要求通信方式占用大的带宽,因此RSS是一个很受欢迎的信号特征,并广泛应用于定位中。
KNN
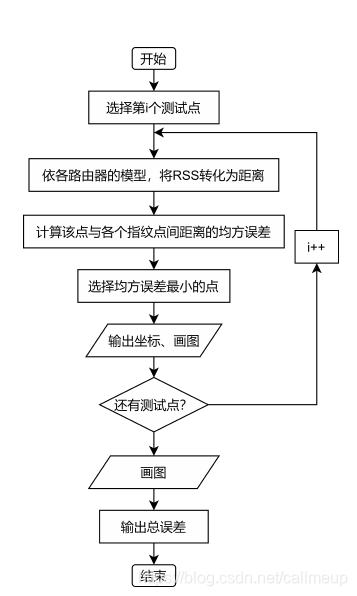
KNN(K-NearesNeighbor,即K邻近法)是一个理论上比较成熟的、也是最简单的机器学习算法之一。用老话就说:“人以群分,物以类聚”。一个样本与数据集中的k个样本最相似, 如果这k个样本中的大多数属于某一个类别, 则该样本也属于这个类别。也就是说,该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别,算法流程图如图:
KNN方法在类别决策时,只与极少量的相邻样本有关。
对数损耗模型
依据信号强度定位,其实质是依据信号能量值随传播距离的增加而衰减的特性来反映出标签与阅读器之间实际的几何距离。因此,信号衰减规律的准确性,直接影响系统定位的准确性。入射信号在室内环境传播的过程中会由于室内障碍物等引起反射、绕射、折射和散射现象而形成多个路径传输,具有不同强度、相位和时延的信号在接收端会叠加形成的衰减的、相位不断变化的信号波形。因此信道衰落统计特性模型的研究主要是多径环境中的幅度衰落。
多径环境中的信号衰落幅度可服从不同分布,这依赖于测量时覆盖的面积,起主导作用的强信号存在与否等。其主要分布包括用于描述平坦衰落信号或独立多径分量接收包络统计时变特性的瑞利分布、描述存在一个主要的静态(非衰落) 信号分量时小尺度衰落包络分布的莱斯分布和对数正态分布7。
假设有一个固定的信号发射源,其平均RSS的衰减和距离的对数成正比,在最简单的情况下,RSSI可以表示为:
R
S
S
I
=
P
t
−
K
−
10
α
l
o
g
10
d
n
RSSI=P_t−K−10 \alpha log_{10}\frac{d}{n}
RSSI=Pt−K−10αlog10nd
其中,
α
\alpha
α称为路径损耗指数,
P
t
P_t
Pt为发送功率,
K
K
K是一个取决于环境和信号频率的常数,
d
d
d为距离,
n
n
n为衰减因子,亦可称为相对距离,经实验,
n
n
n在拟合模型时可以使计算过程更加稳定,一般取2即可。RSSI可以被用来计算移动设备与AP之间的距离。
对数损耗模型是信号发射基站的参数,它受到环境、天气、电磁场干扰等影响,同时当发射源更换或功率变化时,原有的指纹模型即不再适用,损耗模型也应该重新构建8。
数据库建立
RSSI指纹采集
系统的使用分为两个阶段,离线的RSS指纹采集阶段和在线定位阶段。离线阶段,将网络搭建好之后,需要在定位环境中采集大量RP的RSS指纹并存储,RSS指纹地图建好之后才能进入实时定位阶段,指纹地图建立好之后在一段较长的时间内都能使用该地图。
建立指纹数据库是指纹定位方法实现的前提。确定性指纹匹配KNN算法,根据定位点测量的RSSI信号强度与指纹数据库中存储的指纹点 RSSI 信号强度进行匹配,考察定位点与指纹点的相似程度,以此来对定位点的位置进行估计。指纹数据库的建立,首先要按照一定的方法采集处理 RSSI 信号强度,形成指纹数据,然后将指纹数据存储在数据库中,待定位时使用。
坐标定位计算阶段是使用KNN算法和距离权重算法来查找要估算的目标节点的坐标值。首先,参考节点和目标节点之间的欧几里德距离使用最佳估计值计算
在信息楼105实验室
7.483
m
×
3.75
m
7.483m\times 3.75m
7.483m×3.75m的环境中,放置3个路由器用于信号发送,将整个环境分割成如图所示的24个网格,在线条交叉点分别测试每个路由器的RSS数据,形成
横向
6
×
纵向
3
×
3
个路由器
=
54
\text{横向}6\times \text{纵向}3 \times 3\text{个路由器}=54
横向6×纵向3×3个路由器=54组数据,将其命名为fingerprint.采集装置使用wifi模块ESP8266,并使用STM32F103ZET6进行AT命令的发送和数据预处理。
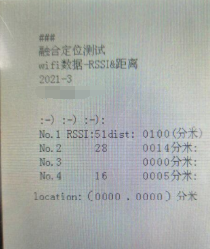
数据由stm32接收后预处理,分拣出有用信息,实时显示在显示屏上,如图:
同时由串口传输至计算机后,在matlab上构建三维数据库,数据如下:
fingerprint(:,:,1) =
-39 ~ -52 ~ -44 ~ -56 ~ -52 ~ -63;
-44 ~ -38 ~ -49 ~ -52 ~ -44 ~ -58;
-38 ~ -35 ~ -36 ~ -49 ~ -50 ~ -51.
fingerprint(:,:,2) =
-44 ~ -43 ~ -39 ~ -37 ~ -44 ~ -38;
-45 ~ -43 ~ -44 ~ -40 ~ -36 ~ -28;
-69 ~ -60 ~ -40 ~ -41 ~ -36 ~ -33.
fingerprint(:,:,3) =
-51 ~ -51 ~ -51 ~ -40 ~ -41 ~ -22;
-62 ~ -56 ~ -48 ~ -51 ~ -65 ~ -31;
-67 ~ -61 ~ -50 ~ -61 ~ -54 ~ -43.
衰减模型建立
RSSI的数据经信号衰减模型换算后可得到近似的距离值。三个路由器分别采集多组RSSI与distance的对应数据,数据如表:
| d(单位是分米) | 路由器1的rssi | 路由器2的rssi | 路由器3的rssi |
|---|---|---|---|
| 1 | 10 | 9 | 11 |
| 1.5 | 18 | 12 | 12 |
| 2 | 14 | 16 | 18 |
| 3 | 19 | 20 | 23 |
| 4 | 19 | 17 | 17 |
| 5 | 21 | 19 | 21 |
| 6 | 23 | 23 | 23 |
| 7 | 24 | 25 | 25 |
| 8 | 23 | 19 | 19 |
| 9 | 25 | 17 | 21 |
| 10 | 16 | 21 | 23 |
| 11 | 26 | 27 | 25 |
| 12 | 28 | 30 | 26 |
| 13 | 25 | 24 | 27 |
| 14 | 26 | 22 | 28 |
| 15 | 26 | 30 | 30 |
| 16 | 27 | 25 | 29 |
| 17 | 26 | 24 | 28 |
| 18 | 25 | 24 | 24 |
| 20 | 28 | 26 | 26 |
| 22 | 32 | 29 | 29 |
| 24 | 26 | 34 | 36 |
| 26 | 27 | 28 | 28 |
| 28 | 28 | 30 | 31 |
| 32 | 38 | 35 | 33 |
| 34 | 27 | 27 | 50 |
| 36 | 36 | 36 | 38 |
| 40 | 31 | 39 | 30 |
| 45 | 31 | 32 | 39 |
| 50 | 43 | 38 | 30 |
| 55 | 33 | 36 | 42 |
| 60 | 34 | 39 | 35 |
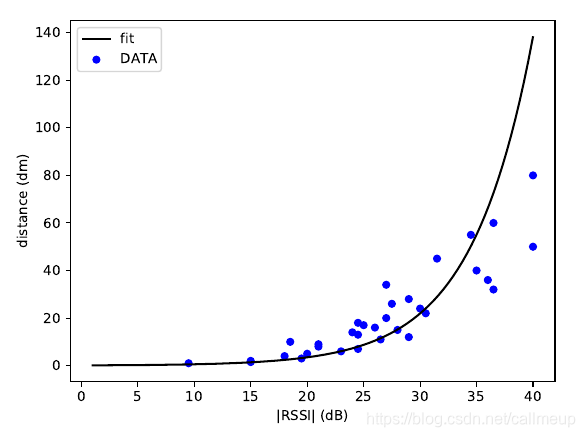
对第一列数据拟合,得到如图\所示的结果:
拟合过程在python里实现,设定模型为:
d
=
2
×
1
0
−
R
S
S
I
+
a
b
d=2\times 10^{\frac{-RSSI+a}{b}}
d=2×10b−RSSI+a,其中,a和b为待定系数,由代码进行最小二乘法求其最优解,直至拟合函数与原有的数据最小均方误差最小,输出a与b的值。
部分程序如下(python):
# edit by callmiaoup
# data 2021.4.20
# modified 2021.7.17
import numpy as np
import matplotlib.pyplot as plt
from scipy import optimize
def func(x, a, b): # 需要拟合的函数
return 2*100 ** ((x+a)/b)
# 拟合点
RSSI = [9.5, 15, 15, 19.5, 18, 20, 23, 24.5, 21, 21, 18.5, 26.5, 29, 24.5, 24, 28 ,26, 25, 24.5, 27, 30.5, 30, 27.5, 29, 36.5, 27, 36, 35, 31.5, 40, 34.5, 36.5, 40]
d = [1, 1.5, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 20, 22, 24, 26, 28, 32, 34, 36, 40, 45, 50, 55, 60, 80]
a4, b4 = optimize.curve_fit(func, d, RSSI, maxfev=500000)[0]
x4 = np.arange(1, 40, 0.01)
y4 = 2*100 ** ((x4-a4)/b4)
plt.figure()
plt.scatter(RSSI[:], d[:], 25, "b")
plt.plot(x4, y4, "k-")
plt.legend(['fit','DATA'])
plt.xlabel('|RSSI| (dB)')
plt.ylabel('distance (dm)')
plt.show()
运用同样的方法可求得其他2个路由器的衰减模型。解得三个路由器的衰减模型表达式,如公式:
R
S
S
I
=
−
17
−
25
l
o
g
10
d
2
R
S
S
I
=
−
17
−
25
l
o
g
10
d
2
R
S
S
I
=
−
17
−
25
l
o
g
10
d
2
RSSI=-17− 25 log_{10}\frac{d}{2}\\ RSSI=-17− 25 log_{10}\frac{d}{2}\\ RSSI=-17− 25 log_{10}\frac{d}{2}\\
RSSI=−17−25log102dRSSI=−17−25log102dRSSI=−17−25log102d
数据测试
在预设环境中实时定位时,matlab中已存入该环境的RSS指纹数据库,3个AP放置在固定位置,用户手持用户节点,用户节点周期性的发送数据,AP收到数据后将自身产生的的RSS信息传入matlab,计算数据后进行定位算法的执行并将定位结果展示出来。
静态功率
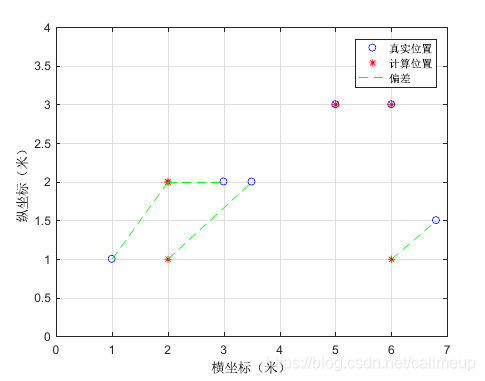
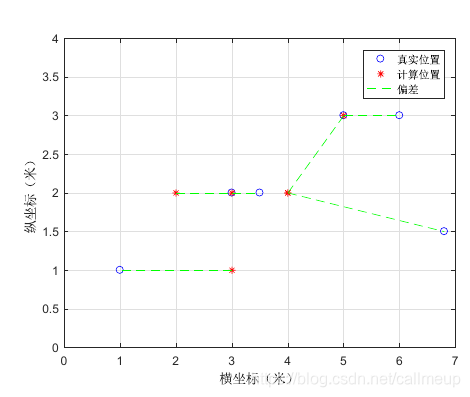
当各个路由器的信号发射功率不变时,即为静态功率下的定位,由matlab进行求解,实验数据来自真实的复杂的环境,求解结果如图所示:
图中圆圈代表所选测试集的真实位置,*号代表由KNN计算而来的位置,虚线连接了真实位置与计算位置,便于辨别对应的点。此方法求得的位置均方误差为0.8601,最大偏差距离为1.8028米。
动态功率
用更换第三台路由器的方法模拟路由器天线故障或更换设备的情况,继续沿用上述方法定位,则会造成误差明显变大,结果如图:
图中圆圈代表所选测试集的真实位置,*号代表由KNN计算而来的位置,虚线连接了真实位置与计算位置,便于辨别对应的点。此方法求得的位置均方误差为1.4598,最大偏差为2.8443米。
重新拟合各路由器信号衰减模型的数据,得下式的结果:
R
S
S
I
=
−
17
−
25
l
o
g
10
d
2
R
S
S
I
=
−
17
−
25
l
o
g
10
d
2
R
S
S
I
=
−
20
−
27
l
o
g
10
d
2
RSSI=-17− 25 log_{10}\frac{d}{2}\\ RSSI=-17− 25 log_{10}\frac{d}{2}\\ RSSI=-20− 27 log_{10}\frac{d}{2}\\
RSSI=−17−25log102dRSSI=−17−25log102dRSSI=−20−27log102d
将原有的RSS-位置指纹的定位方法更改为RSS-距离-位置指纹的方法,在matlab源码中加入距离衰减模型公式:
fingerprint_d=2.*power(10,
(-fingerprint-17)/25);
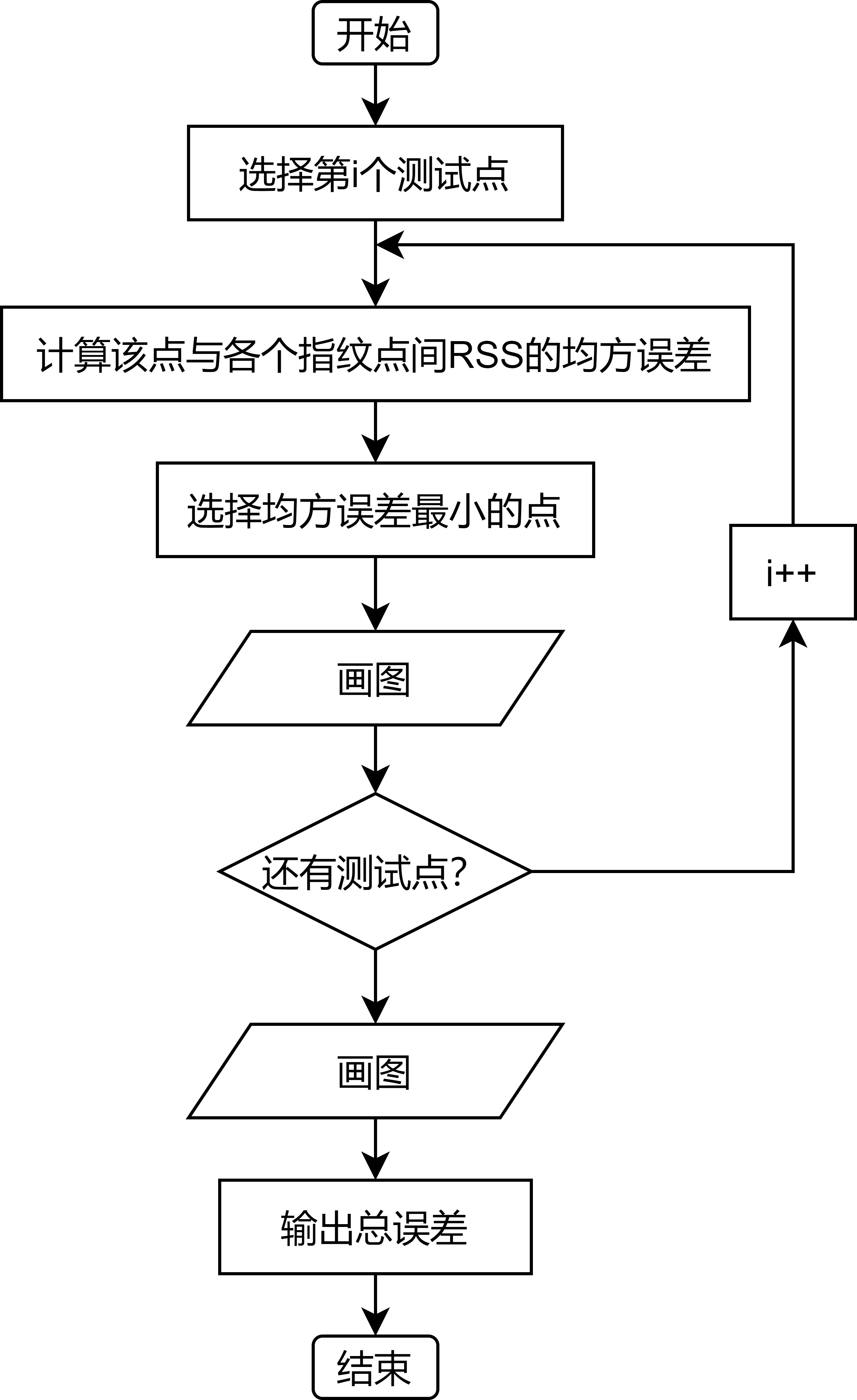
即可批量将指数表示的信号强度批量转化为距离数组,从而由RSS指纹转变为距离指纹,修改原有算法思想,如图:
原有定位按照RSSI来作为指纹,虽然数据的采集较为方便,但是一旦有信号发射器故障,或者更换了部分发射器,整个指纹库(至少有一个维度)的所有指纹数据均需要修改,维护成本过高。但是如果将每个RSSI换算为距离,再根据距离指纹定位,可以减少人工更新指纹库的繁琐工作。
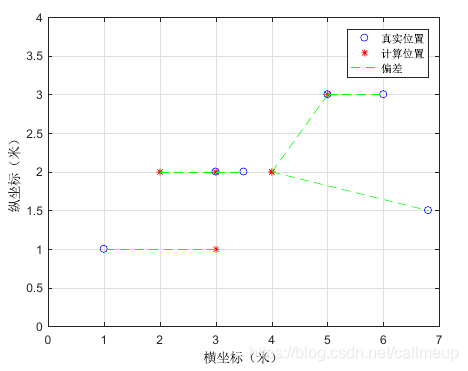
重新获取测试集中对应路由器3的RSS,用上述方法定位的结果如图:
图中圆圈代表所选测试集的真实位置,*号代表由KNN计算而来的位置,虚线连接了真实位置与计算位置,便于辨别对应的点。此方法求得的位置均方误差为1.1934,最大偏差为2米,两项指标均优于传统的指纹定位。
结论
本文分别实现了基于RSS位置指纹的室内定位系统,基于RSSI与距离的非线性拟合,以及基于距离位置指纹的定位系统。主要贡献为:针对位置指纹法在实际运用中可能存在的问题,引入RSS-距离-指纹模型,改进模型计算出的位置坐标更接近实际坐标,这使得定位精度更高。
实验结果表明,与传统的定位算法相比,该算法的定位精度显著提高9。
K邻近法分类经常被用于定位算法进行研究,但是很多人对此的研究仅仅止步于模拟与仿真,本文用实际采集的数据进行实验,用更真实的结果证明了算法的可行性。
源代码
拟合数据的代码:
# edit by callmiaoup
# data 2021.4.20
# modified 2021.7.17
import numpy as np
import matplotlib.pyplot as plt
from scipy import optimize
def func(x, a, b): # 需要拟合的函数
return 2*100 ** ((x+a)/b)
# 拟合点
RSSI = [9.5, 15, 15, 19.5, 18, 20, 23, 24.5, 21, 21, 18.5, 26.5, 29, 24.5, 24, 28 ,26, 25, 24.5, 27, 30.5, 30, 27.5, 29, 36.5, 27, 36, 35, 31.5, 40, 34.5, 36.5, 40]
d = [1, 1.5, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 20, 22, 24, 26, 28, 32, 34, 36, 40, 45, 50, 55, 60, 80]
a4, b4 = optimize.curve_fit(func, d, RSSI, maxfev=500000)[0]
x4 = np.arange(1, 40, 0.01)
y4 = 2*100 ** ((x4-a4)/b4)
plt.figure()
plt.scatter(RSSI[:], d[:], 25, "b")
plt.plot(x4, y4, "k-")
plt.legend(['fit','DATA'])
plt.xlabel('|RSSI| (dB)')
plt.ylabel('distance (dm)')
plt.show()
指纹定位的代码: 下载链接.
Location Based Service,基于位置的服务。 ↩︎
Cai C, Gao Y, Pan L, et al. Precise point positioning with quad-constellations: GPS, BeiDou, GLONASS and Galileo[J]. Advances in space research, 2015, 56(1): 133-143. ↩︎
Received Signal Strength Indicator,接收信号强度的强度指示。 ↩︎
涂维娟,郭承军. 基于机器学习的室内定位方法综述[A]. 中国卫星导航系统管理办公室学术交流中心.第十二届中国卫星导航年会论文集——S09 用户终端技术[C].中国卫星导航系统管理办公室学术交流中心:中国卫星导航学术年会组委会,2021:6. ↩︎
Received Signal Strength,接收信号强度。 ↩︎
Zekavat S R, Buehrer R M, Durgin G D, et al. An Overview on Position Location: Past, Present, Future[J]. International Journal of Wireless Information Networks, 2021: 1-32. ↩︎
胡晓菲.对数路径改进模型室内定位算法[J].电声技术,2015,39(06):37-39. ↩︎
Ji Y, Biaz S, Pandey S, et al. ARIADNE: a dynamic indoor signal map construction and localization system[C]//Proceedings of the 4th international conference on Mobile systems, applications and services. 2006: 151-164. ↩︎
Cui X, Wang M, Li J, et al. Indoor Wi-Fi Positioning Algorithm Based on Location Fingerprint[J]. Mobile Networks and Applications, 1-10. ↩︎