本代码使用MATLAB实现扩展卡尔曼滤波（EKF）和粒子滤波（PF）在状态估计中的对比分析。

总述

代码主要功能包括：

参数设置：初始化仿真参数，如粒子数量、时间序列、状态转移与观测噪声的协方差矩阵。
真实状态与观测值生成：通过定义状态转移方程，生成系统的真实状态和带噪声的观测值。
粒子滤波初始化：随机生成粒子并计算初始权重，为粒子滤波的后续步骤做准备。
扩展卡尔曼滤波：通过预测、更新步骤，利用测量数据不断修正状态估计。
粒子滤波实现：在每个时间步中，将粒子进行预测、加权、归一化和重采样，得到状态估计。
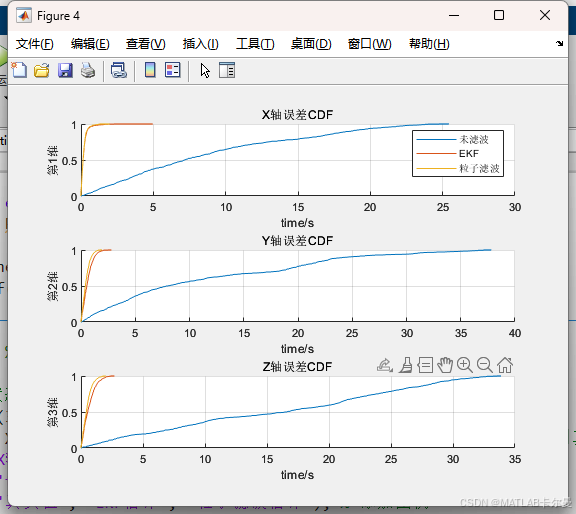
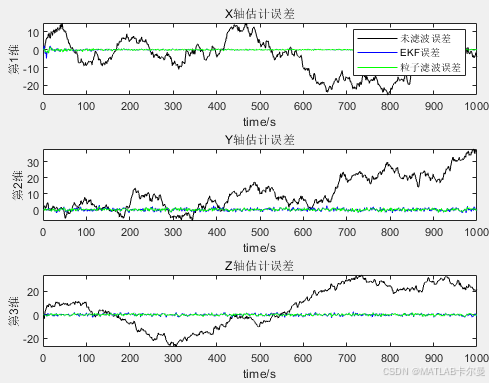
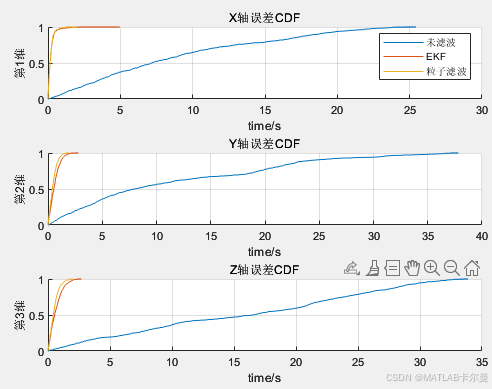
绘图：绘制真实状态与估计状态的对比图、估计误差图及误差的CDF（累积分布函数）图，方便分析不同滤波方法的性能。
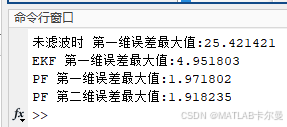
误差统计特性输出：在命令行输出未滤波、EKF和PF的最大误差值，提供对比依据。

部分源代码

如下：

% EKF+PF效果对比
% author:Evand
% date: 2024-1-10
% Ver2
% 2024-09-23/Ver3：添加逐行注释
clear; %清空工作区
clc; %清空命令行
close all; %关闭所有窗口（主窗口除外）
rng(0); %固定随机种子，让每次运行得到的结果相同 
%% 参数设置
N = 100; %粒子总数（此值仅影响粒子滤波部分）
t = 1:1:1000; %仿真时间设置
Q = 1*diag([1,1,1]); %设置状态转移协方差矩阵
R = 1*diag([1,1,1]); %设置观测噪声协方差矩阵
w_pf=sqrt(Q)*randn(size(Q,1),length(t)); %生成状态转移噪声
v_pf=sqrt(R)*randn(size(R,1),length(t)); %生成观测噪声
P0 = 1*eye(3); %生成状态协方差矩阵

如上，几乎每一行代码都有中文注释，方便理解。
完整代码下载链接：https://download.csdn.net/download/callmeup/89788619

运行结果

• 三轴状态量对比：
  

• 三轴误差对比：
  

• 三轴误差的CDF图像对比：
  

• 输出误差
  

扩展性

在扩展卡尔曼滤波（Extended Kalman Filter，$EKF$）和粒子滤波（Particle Filter，$PF$）这两种常用的非线性滤波方法之间，有以下几点对比和扩展考虑：

1. 线性假设 vs 非线性处理:
   EKF基于线性化处理，适合系统模型接近线性的场景，但在高度非线性的情况下可能会失效，因为局部线性近似可能导致较大误差。
   PF则天然适用于非线性系统，因为它通过模拟大量的随机采样点（粒子）来追踪不确定性，而非依赖于系统方程的线性性质。

2. 计算效率:
   EKF由于只需要求解一次矩阵运算，相比PF而言，其计算量较小，尤其是在高维系统中。
   粒子滤波的计算复杂度随着粒子数目的增加而增加，当系统状态维度很高或观测噪声大时，可能需要大量粒子才能保持较好的估计精度。

3. 鲁棒性和适应性:
   PF对初始条件敏感度较低，且能较好地处理缺失数据和异常值，适合不确定性较高的环境。
   EKF在某些极端条件下（如矩阵奇异），可能会导致滤波器不稳定。

4. 扩展性:
   EKF通常更容易与已有的数学工具结合，比如系统动力学建模等。
   PF的扩展性相对较弱，但随着算法优化（如Resampling、Bootstrap Sampling等）和并行计算的发展，现代PF技术也有了改进。

为了进一步扩展这两种滤波器，可以考虑：

1. 融合信息: 结合其他滤波方法（如无迹卡尔曼滤波Unscented Kalman Filter, UKF），增强非线性处理能力。
2. 自适应采样: 对于粒子滤波，研究更高效的采样策略和重采样方法，降低计算成本。
3. 在线学习: 在EKF中引入机器学习元素，提高对未知动态模型的适应能力。
4. 硬件加速: 为大数据量的PF设计专用硬件或者GPU加速算法。
5. 深度学习辅助: 将滤波结果作为神经网络训练的数据输入，提升整体系统的性能。

如有需求，可通过问文末卡片联系作者