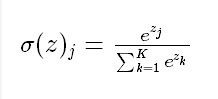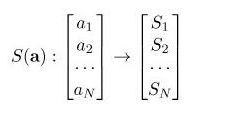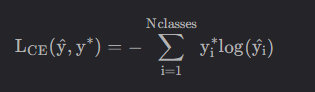文章目录
0 前言
🔥 这两年开始毕业设计和毕业答辩的要求和难度不断提升，传统的毕设题目缺少创新和亮点，往往达不到毕业答辩的要求，这两年不断有学弟学妹告诉学长自己做的项目系统达不到老师的要求。
为了大家能够顺利以及最少的精力通过毕设，学长分享优质毕业设计项目，今天要分享的是
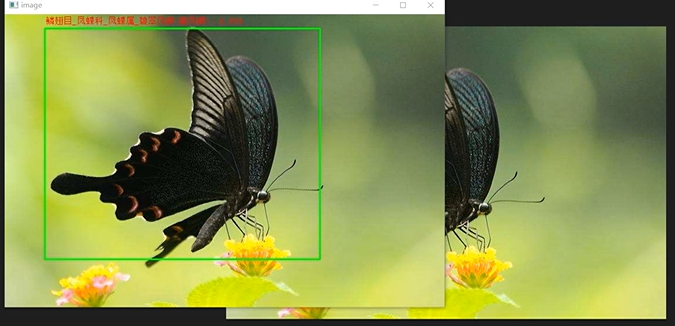
🚩 **基于深度学习的昆虫识别算法研究与实现 **
🥇学长这里给一个题目综合评分(每项满分5分)
- 难度系数：3分
- 工作量：4分
- 创新点：4分
1 课题背景
中国是农业大国，在传统的农业生产中，经常会受到病虫害问题的困扰。在解决病虫害问题时，第一步是识别昆虫。在传统的昆虫识别方法中，昆虫专家根据专业知识观察昆虫的外部特征，并对照相关的昆虫图鉴进行识别，费时费力。如今，传统的昆虫识别方法逐渐被昆虫图像识别技术代替。目前常用的昆虫识别技术有图像识别法、微波雷达检测法、生物光子检测法、取样检测法、近红外及高光谱法、声测法等。近年来，随着人工智能的迅速发展，深度学习技术在处理自然语言、机器视觉等方面取得了很多成果，随着深度学习的发展，已经有研究人员开始将深度学习技术应用于昆虫的图像识别。文章旨在利用基于深度学习的图像识别技术解决昆虫识别问题，希望能给现实生活中的病虫害识别问题提供新的解决问题的思路。
2 具体实现
3 数据收集和处理
数据是深度学习的基石
数据的主要来源有: 百度图片, 必应图片, 新浪微博, 百度贴吧, 新浪博客和一些专业的昆虫网站等
爬虫爬取的图像的质量参差不齐, 标签可能有误, 且存在重复文件, 因此必须清洗。清洗方法包括自动化清洗, 半自动化清洗和手工清洗。
自动化清洗包括:
- 滤除小尺寸图像.
- 滤除宽高比很大或很小的图像.
- 滤除灰度图像.
- 图像去重: 根据图像感知哈希.
半自动化清洗包括:
- 图像级别的清洗: 利用预先训练的昆虫/非昆虫图像分类器对图像文件进行打分, 非昆虫图像应该有较低的得分; 利用前一阶段的昆虫分类器对图像文件 (每个文件都有一个预标类别) 进行预测, 取预标类别的概率值为得分, 不属于原预标类别的图像应该有较低的得分. 可以设置阈值, 滤除很低得分的文件; 另外利用得分对图像文件进行重命名, 并在资源管理器选择按文件名排序, 以便于后续手工清洗掉非昆虫图像和不是预标类别的图像.
- 类级别的清洗
手工清洗: 人工判断文件夹下图像是否属于文件夹名所标称的物种, 这需要相关的昆虫学专业知识, 是最耗时且枯燥的环节。
3 卷积神经网络
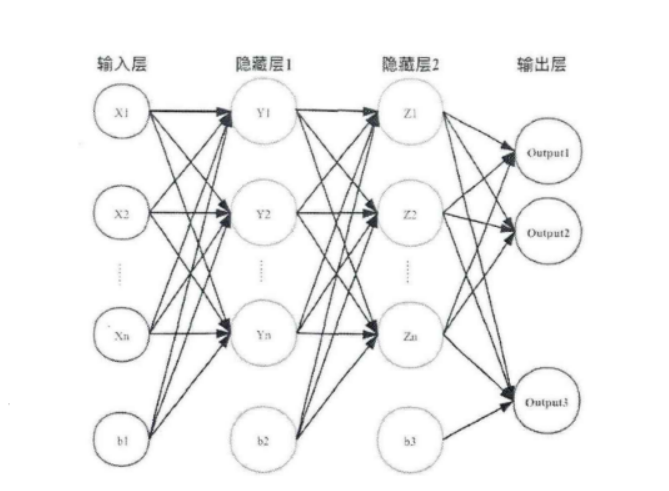
卷积神经网络（Convolutional Neural Netwoek，CNN）是一种前馈神经网络，它的人工神经元可以局部响应周围的神经元，每个神经元都接收一些输入，并做一些点积计算。它通常包含卷积层、激活层、池化层、全连接层。
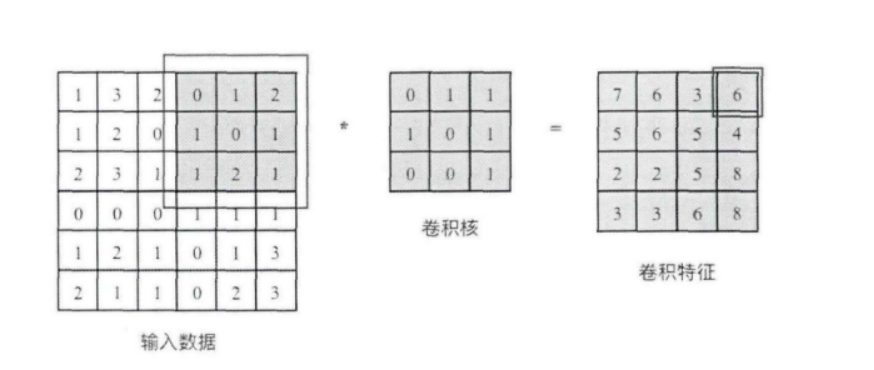
2.1卷积层
卷积核相当于一个滑动窗口，示意图中３x３大小的卷积核依次划过６x６大小的输入数据中的对应区域，并与卷积核滑过区域做矩阵点乘，将所得结果依次填入对应位置即可得到右侧４x４尺寸的卷积特征图，例如划到右上角３x３所圈区域时，将进行０x０＋１x１＋２x１＋１x１＋０x０＋１x１＋１x０＋２x０x１x１＝６的计算操作，并将得到的数值填充到卷积特征的右上角。
2.2 池化层
池化操作又称为降采样，提取网络主要特征可以在达到空间不变性的效果同时，有效地减少网络参数，因而简化网络计算复杂度，防止过拟合现象的出现。在实际操作中经常使用最大池化或平均池化两种方式，如下图所示。虽然池化操作可以有效的降低参数数量，但过度池化也会导致一些图片细节的丢失，因此在搭建网络时要根据实际情况来调整池化操作。[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-UTsB7AhE-1658995487680)
![(C:\Users\Administrator\AppData\Roaming\Typora\typora-user-images\image-20220709114210181.png)]](/image/aHR0cHM6Ly9pbWctYmxvZy5jc2RuaW1nLmNuLzdlZjk4ODliYTVjNTQzNGU4ZDNkODcwMzRlZjdhMTU0LnBuZw%3D%3D)
2.3 激活函数：
激活函数大致分为两种，在卷积神经网络的发展前期，使用较为传统的饱和激活函数，主要包括sigmoid函数、tanh函数等；随着神经网络的发展，研宄者们发现了饱和激活函数的弱点，并针对其存在的潜在问题，研宄了非饱和激活函数，其主要含有ReLU函数及其函数变体
2.4 全连接层
在整个网络结构中起到“分类器”的作用，经过前面卷积层、池化层、激活函数层之后，网络己经对输入图片的原始数据进行特征提取，并将其映射到隐藏特征空间，全连接层将负责将学习到的特征从隐藏特征空间映射到样本标记空间，一般包括提取到的特征在图片上的位置信息以及特征所属类别概率等。将隐藏特征空间的信息具象化，也是图像处理当中的重要一环。
2.5 使用tensorflow中keras模块实现卷积神经网络
class CNN(tf.keras.Model):
def __init__(self):
super().__init__()
self.conv1 = tf.keras.layers.Conv2D(
filters=32, # 卷积层神经元（卷积核）数目
kernel_size=[5, 5], # 感受野大小
padding='same', # padding策略（vaild 或 same）
activation=tf.nn.relu # 激活函数
)
self.pool1 = tf.keras.layers.MaxPool2D(pool_size=[2, 2], strides=2)
self.conv2 = tf.keras.layers.Conv2D(
filters=64,
kernel_size=[5, 5],
padding='same',
activation=tf.nn.relu
)
self.pool2 = tf.keras.layers.MaxPool2D(pool_size=[2, 2], strides=2)
self.flatten = tf.keras.layers.Reshape(target_shape=(7 * 7 * 64,))
self.dense1 = tf.keras.layers.Dense(units=1024, activation=tf.nn.relu)
self.dense2 = tf.keras.layers.Dense(units=10)
def call(self, inputs):
x = self.conv1(inputs) # [batch_size, 28, 28, 32]
x = self.pool1(x) # [batch_size, 14, 14, 32]
x = self.conv2(x) # [batch_size, 14, 14, 64]
x = self.pool2(x) # [batch_size, 7, 7, 64]
x = self.flatten(x) # [batch_size, 7 * 7 * 64]
x = self.dense1(x) # [batch_size, 1024]
x = self.dense2(x) # [batch_size, 10]
output = tf.nn.softmax(x)
return output
4 MobileNetV2网络
简介
MobileNet网络是Google最近提出的一种小巧而高效的CNN模型，其在accuracy和latency之间做了折中。
主要改进点
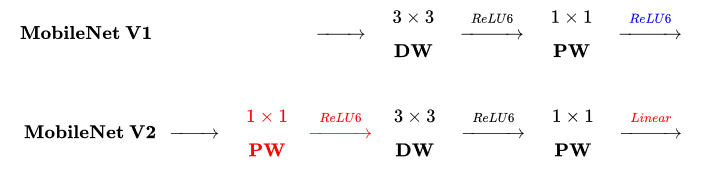
相对于MobileNetV1，MobileNetV2 主要改进点：
- 引入倒残差结构，先升维再降维，增强梯度的传播，显著减少推理期间所需的内存占用（Inverted Residuals）
- 去掉 Narrow layer(low dimension or depth) 后的 ReLU，保留特征多样性，增强网络的表达能力（Linear Bottlenecks）
- 网络为全卷积，使得模型可以适应不同尺寸的图像；使用 RELU6（最高输出为 6）激活函数，使得模型在低精度计算下具有更强的鲁棒性
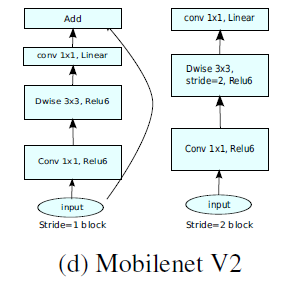
- MobileNetV2 Inverted residual block 如下所示，若需要下采样，可在 DW 时采用步长为 2 的卷积
- 小网络使用小的扩张系数（expansion factor），大网络使用大一点的扩张系数（expansion factor），推荐是5~10，论文中 t = 6 t = 6t=6
倒残差结构（Inverted residual block）
ResNet的Bottleneck结构是降维->卷积->升维，是两边细中间粗
而MobileNetV2是先升维（6倍）-> 卷积 -> 降维，是沙漏形。
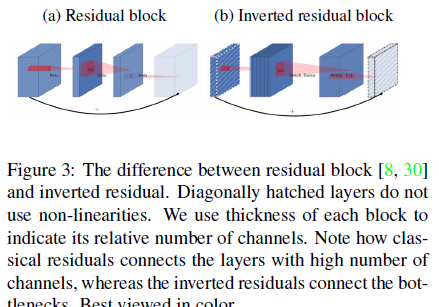
因为DW卷积不改变通道数，所以如果上一层的通道数很低时，DW只能在低维空间提取特征，效果不好。所以V2版本在DW前面加了一层PW用来升维。
同时V2去除了第二个PW的激活函数改用线性激活，因为激活函数在高维空间能够有效地增加非线性，但在低维空间时会破坏特征。由于第二个PW主要的功能是降维，所以不宜再加ReLU6。
tensorflow相关实现代码
import tensorflow as tf
import numpy as np
from tensorflow.keras import layers, Sequential, Model
class ConvBNReLU(layers.Layer):
def __init__(self, out_channel, kernel_size=3, strides=1, **kwargs):
super(ConvBNReLU, self).__init__(**kwargs)
self.conv = layers.Conv2D(filters=out_channel,
kernel_size=kernel_size,
strides=strides,
padding='SAME',
use_bias=False,
name='Conv2d')
self.bn = layers.BatchNormalization(momentum=0.9, epsilon=1e-5, name='BatchNorm')
self.activation = layers.ReLU(max_value=6.0) # ReLU6
def call(self, inputs, training=False, **kargs):
x = self.conv(inputs)
x = self.bn(x, training=training)
x = self.activation(x)
return x
class InvertedResidualBlock(layers.Layer):
def __init__(self, in_channel, out_channel, strides, expand_ratio, **kwargs):
super(InvertedResidualBlock, self).__init__(**kwargs)
self.hidden_channel = in_channel * expand_ratio
self.use_shortcut = (strides == 1) and (in_channel == out_channel)
layer_list = []
# first bottleneck does not need 1*1 conv
if expand_ratio != 1:
# 1x1 pointwise conv
layer_list.append(ConvBNReLU(out_channel=self.hidden_channel, kernel_size=1, name='expand'))
layer_list.extend([
# 3x3 depthwise conv
layers.DepthwiseConv2D(kernel_size=3, padding='SAME', strides=strides, use_bias=False, name='depthwise'),
layers.BatchNormalization(momentum=0.9, epsilon=1e-5, name='depthwise/BatchNorm'),
layers.ReLU(max_value=6.0),
#1x1 pointwise conv(linear)
# linear activation y = x -> no activation function
layers.Conv2D(filters=out_channel, kernel_size=1, strides=1, padding='SAME', use_bias=False, name='project'),
layers.BatchNormalization(momentum=0.9, epsilon=1e-5, name='project/BatchNorm')
])
self.main_branch = Sequential(layer_list, name='expanded_conv')
def call(self, inputs, **kargs):
if self.use_shortcut:
return inputs + self.main_branch(inputs)
else:
return self.main_branch(inputs)
5 损失函数softmax 交叉熵
5.1 softmax函数
Softmax函数由下列公式定义
softmax 的作用是把 一个序列，变成概率。
softmax用于多分类过程中，它将多个神经元的输出，映射到（0,1）区间内，所有概率的和将等于1。
python实现
def softmax(x):
shift_x = x - np.max(x) # 防止输入增大时输出为nan
exp_x = np.exp(shift_x)
return exp_x / np.sum(exp_x)
PyTorch封装的Softmax()函数
dim参数：
- dim为0时，对所有数据进行softmax计算
- dim为1时，对某一个维度的列进行softmax计算
- dim为-1 或者2 时，对某一个维度的行进行softmax计算
import torch
x = torch.tensor([2.0,1.0,0.1])
x.cuda()
outputs = torch.softmax(x,dim=0)
print("输入：",x)
print("输出：",outputs)
print("输出之和：",outputs.sum())
5.2 交叉熵损失函数
定义如下:
python实现
def cross_entropy(a, y):
return np.sum(np.nan_to_num(-y*np.log(a)-(1-y)*np.log(1-a)))
# tensorflow version
loss = tf.reduce_mean(-tf.reduce_sum(y_*tf.log(y), reduction_indices=[1]))
# numpy version
loss = np.mean(-np.sum(y_*np.log(y), axis=1))
PyTorch实现
交叉熵函数分为二分类(torch.nn.BCELoss())和多分类函数(torch.nn.CrossEntropyLoss()
# 二分类 损失函数
loss = torch.nn.BCELoss()
l = loss(pred，real)
# 多分类损失函数
loss = torch.nn.CrossEntropyLoss()
6 优化器SGD
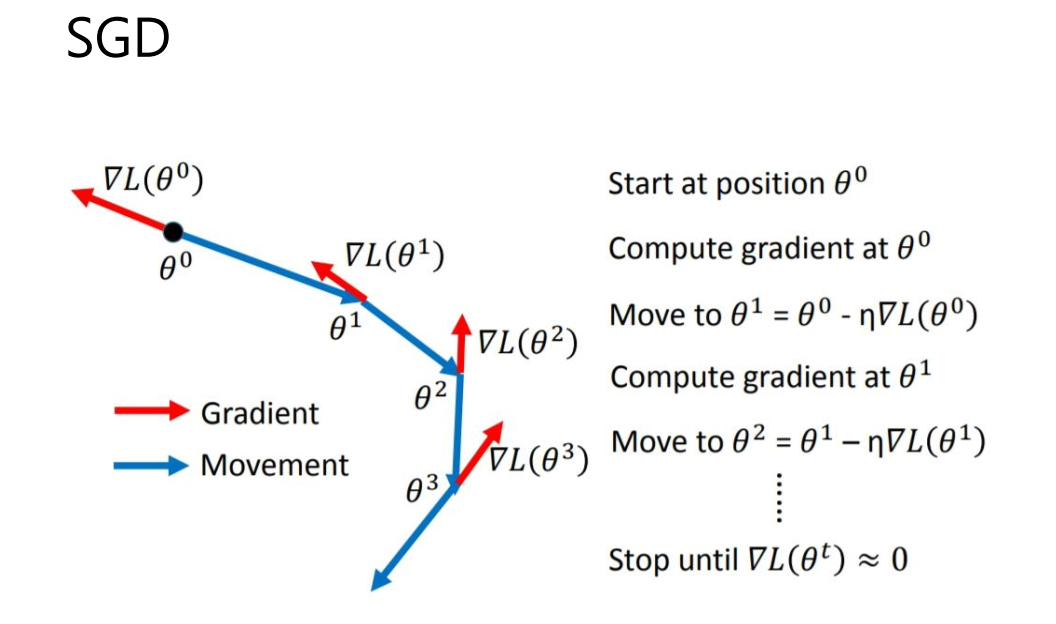
简介
SGD全称Stochastic Gradient Descent，随机梯度下降，1847年提出。每次选择一个mini-batch，而不是全部样本，使用梯度下降来更新模型参数。它解决了随机小批量样本的问题，但仍然有自适应学习率、容易卡在梯度较小点等问题。
pytorch调用方法：
torch.optim.SGD(params, lr=<required parameter>, momentum=0, dampening=0, weight_decay=0, nesterov=False)
相关代码：
def step(self, closure=None):
"""Performs a single optimization step.
Arguments:
closure (callable, optional): A closure that reevaluates the model
and returns the loss.
"""
loss = None
if closure is not None:
loss = closure()
for group in self.param_groups:
weight_decay = group['weight_decay'] # 权重衰减系数
momentum = group['momentum'] # 动量因子，0.9或0.8
dampening = group['dampening'] # 梯度抑制因子
nesterov = group['nesterov'] # 是否使用nesterov动量
for p in group['params']:
if p.grad is None:
continue
d_p = p.grad.data
if weight_decay != 0: # 进行正则化
# add_表示原处改变，d_p = d_p + weight_decay*p.data
d_p.add_(weight_decay, p.data)
if momentum != 0:
param_state = self.state[p] # 之前的累计的数据，v(t-1)
# 进行动量累计计算
if 'momentum_buffer' not in param_state:
buf = param_state['momentum_buffer'] = torch.clone(d_p).detach()
else:
# 之前的动量
buf = param_state['momentum_buffer']
# buf= buf*momentum + （1-dampening）*d_p
buf.mul_(momentum).add_(1 - dampening, d_p)
if nesterov: # 使用neterov动量
# d_p= d_p + momentum*buf
d_p = d_p.add(momentum, buf)
else:
d_p = buf
# p = p - lr*d_p
p.data.add_(-group['lr'], d_p)
return loss
7 学习率衰减策略
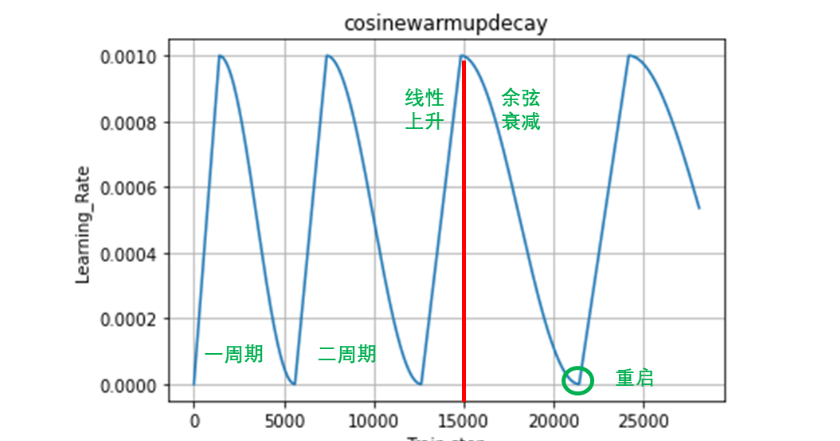
余弦退火衰减
这可以理解为是一种带重启的随机梯度下降算法。在网络模型更新时，由于存在很多局部最优解，这就导致模型会陷入局部最优解，即优化函数存在多个峰值。这就要求，当模型陷入局部最优解时，能够跳出去，并且继续寻找下一个最优解，直到找到全局最优解。要使得模型跳出局部最优解，就需要在模型陷入局部最优解时突然提高学习率，即重启学习率。
多周期的余弦退火衰减示意图如下：
相关代码实现
# ----------------------------------------------------------------------- #
# 多周期余弦退火衰减
# ----------------------------------------------------------------------- #
# eager模式防止graph报错
tf.config.experimental_run_functions_eagerly(True)
# ------------------------------------------------ #
import math
# 继承自定义学习率的类
class CosineWarmupDecay(keras.optimizers.schedules.LearningRateSchedule):
'''
initial_lr: 初始的学习率
min_lr: 学习率的最小值
max_lr: 学习率的最大值
warmup_step: 线性上升部分需要的step
total_step: 第一个余弦退火周期需要对总step
multi: 下个周期相比于上个周期调整的倍率
print_step: 多少个step并打印一次学习率
'''
# 初始化
def __init__(self, initial_lr, min_lr, warmup_step, total_step, multi, print_step):
# 继承父类的初始化方法
super(CosineWarmupDecay, self).__init__()
# 属性分配
self.initial_lr = tf.cast(initial_lr, dtype=tf.float32)
self.min_lr = tf.cast(min_lr, dtype=tf.float32)
self.warmup_step = warmup_step # 初始为第一个周期的线性段的step
self.total_step = total_step # 初始为第一个周期的总step
self.multi = multi
self.print_step = print_step
# 保存每一个step的学习率
self.learning_rate_list = []
# 当前步长
self.step = 0
# 前向传播, 训练时传入当前step，但是上面已经定义了一个，这个step用不上
def __call__(self, step):
# 如果当前step达到了当前周期末端就调整
if self.step>=self.total_step:
# 乘上倍率因子后会有小数，这里要注意
# 调整一个周期中线性部分的step长度
self.warmup_step = self.warmup_step * (1 + self.multi)
# 调整一个周期的总step长度
self.total_step = self.total_step * (1 + self.multi)
# 重置step，从线性部分重新开始
self.step = 0
# 余弦部分的计算公式
decayed_learning_rate = self.min_lr + 0.5 * (self.initial_lr - self.min_lr) * \
(1 + tf.math.cos(math.pi * (self.step-self.warmup_step) / \
(self.total_step-self.warmup_step)))
# 计算线性上升部分的增长系数k
k = (self.initial_lr - self.min_lr) / self.warmup_step
# 线性增长线段 y=kx+b
warmup = k * self.step + self.min_lr
# 以学习率峰值点横坐标为界，左侧是线性上升，右侧是余弦下降
decayed_learning_rate = tf.where(self.step<self.warmup_step, warmup, decayed_learning_rate)
# 每个epoch打印一次学习率
if step % self.print_step == 0:
# 打印当前step的学习率
print('learning_rate has changed to: ', decayed_learning_rate.numpy().item())
# 每个step保存一次学习率
self.learning_rate_list.append(decayed_learning_rate.numpy().item())
# 计算完当前学习率后step加一用于下一次
self.step = self.step + 1
# 返回调整后的学习率
return decayed_learning_rate