摘要:
本文回顾了TD-SCDMA中用于多用户检测的迫零块线性均衡(ZF-BLE)技术,着重分析了用于解最小均方估计矩阵方程的近似Cholesky 因式分解法,并确定了这种算法需要达到的近似度。 本文将这种方法与ZF-BLE中最常用的方法相比较,从而证明,与在TDD 模式的高码速率中表现出的特性不同,这种方法可获得最低的计算复杂度,并显示出近似理想的比特误码率性能。
引言
众所周知, TD-SCDMA [1] 的(NodeB或终端)接收机要求使用多用户(联合检测)以提供满足通信传输要求的链路性能。[5] 中介绍了4种类型已实现的、高性能的联合检测器。 这些都是基于迫零或最小均方误差块线性预测, 其中包括使用和未使用决策反馈的2种情况 ( [5]中分别记作ZF-BLE, MMSE-BLE, ZF-BDFE, MMSE-BDFE)。在 [6] 中,给出2个简化的相关检测器,但仅适用于只有一个发射天线的情况。 因为这种情形等于排除了智能天线技术的使用——这是TD-SCDMA的一个标志性的技术,使得我们无法采用这2个简化检测器的分析。
[5] 的作者和其它研究论文的作者,如[7]的作者, 发现ZF-BLE 检测器能够提供远远超出常规RAKE接收机及决策反馈扩展RAKE接收机的优异性能。 并且,这些作者也发现,其它3种比ZF-BLE 检测器更复杂的联合检测器(MMSE-BLE, ZF-BDFE, and MMSE-BDFE)在性能上比ZF-BLE 检测器的改进相对很小。 因而, 可以认为,ZF-BLE 检测器是适用于TD-SCDMA 系统的标准检测器。 尽管这种检测器的复杂度是所有高性能联合检测器中最低的,但在实现过程中, 考虑到待机时间等性能指标的要求,降低这种联合检测器的复杂度仍是一个非常关键的问题。
为求解ZF-BLE 方程,研究人员提出各种方法( 见 [8], [9], [10] 及相关文献) 。本文回顾了最先由[9] 提出的,基于近似Cholesky 因式分解的算法,并给出针对TD-SCDMA 系统的浮点仿真结果,以确定因式分解需要达到的近似度。 本文将这种方法与ZF-BLE中最常用的方法相比较,从而证明,与在TDD 模式的高码速率中表现出的特性不同,这种方法可以给出最低的计算复杂度,和近似于理想的比特误码率性能。
下一节描述TD-SCDMA下行链路信号模型,之后用一节详细阐述使用近似Cholesky 因式分解的ZF-BLE 检测器。 随后的部分给出了这种算法的复杂度分析,并介绍了其它4种解ZF-BLE 方程的主要方法, 从而比较了全部的5种方法的计算复杂度。最后的2部分给出了仿真性能结果和结论。
本节,我们将详细比较Cholesky 算法及其它4种解ZF-BLE 方程的最重要算法: Block-Levinson 算法, Block-Schur 算法, Block-Fourier 算法, 以及 Fourier-Block 算法。 [8] 中针对TD-SCDMA讨论并比较Block-Levinson 算法, Block-Schur 算法, Block-Fourier 算法,Cholesky 算法。[10] 提出和分析了Fourier-Block 算法。
Levinson 算法
Levinson 算法可用于计算具有厄密共轭、Toeplitz的nхn维正定矩阵的线性方程系统的解,计算操作次数只有O(n2) 幂次。 Block-Levinson 算法是Levinson 算法的扩展,用于矩阵是block-Toeplitz的情况。 Block-Levinson 算法是递归算法,是对KхK 维矩阵做N 次主迭代计算。 可以使用Block-Levinson近似算法计算线性方程的解,即在经过若干次主循环的迭代计算后,将2个内部参数(α 、 η) 置成零。更进一步的近似算法是截短2个内部块矢量(Y 、 W) 操作处理的长度。 在后文中, “n 迭代” 的意思是:在n-1次迭代后, α 、 η 被置成0 ,并且每次迭代过程更新Y 和 W 的n 个块[8]。
Schur Algorithm
Schur 算法可以高效地找到系统矩阵A的QR 表示中的三角因子R ,其中, R 也是S的Cholesky 因子。 Block-Schur 算法用于计算S 的一种变换形式,这种变换形式的重要特点是其冗余度小于S 。 矩阵 R 可以写成块行矩阵的形式,并且与近似 Cholesky 算法中的情况类似,它也可以使用近似的算法,在计算出足够的块行之后就可以给出具有足够近似度的求解结果[11]。
Block-Fourier 算法
在 Block-Fourier 算法中,系统矩阵 A 扩展成 块-循环矩阵 (这引入了近似) ,并且用block-Fourier 变换 (用 FFTs 实现) 将ZF-BLE 方程变成 块-对角矩阵。然而,沿着变换后的块对角矩阵的对角的子阵是无结构的,且要使用非近似的Cholesky 分解进行转换。可以将数据矢量分割成小块,以进一步减少计算开销, 同时要使用重叠保留技术避免由于数据分割造成的边缘扭曲[8]。在下文中,将分割块记作(FFT length, pre-lap, post-lap)。
Fourier-Block算法
作为我们最后谈到的算法, 与Block-Fourier 算法的不同之处是:在 Fourier-Block算法中,重新组织数据矢量的目的,不是为了获得block-Toeplitz 系统矩阵,而是为了获得Toeplitz-block结构 [5]。由此产生的相关矩阵 S由 K2 个Toeplitz NхN 维子阵构成。每一个子阵可以近似成循环矩阵,用Fourier 变换将它们对角化。因此, 在 频率-空间范围中, S 由 K2 个NхN 维对角子阵构成。可以用 O(K3N) 次操作完成这个矩阵的Cholesky 因式分解。 然后可以用前向替换和后向替换在频率-空间范围内解ZF-BLE 方程[10]。
计算复杂度
尽管2个基于Fourier变换的方法也使用Cholesky 因式分解,但除非特地说明,本文中提到的 “Cholesky 算法” 指的是使用第0 节中详细阐述的近似Cholesky 因式分解的直接方法(非Fourier方法) 。
我们记得, TD-SCDMA 是低码片速率,而TD-CDMA 高码片速率。 在 [8], [9] 和 [10] 中讨论的TD-CDMA , 由于高码片速率,其 W 是很高的 (等于 57) ,而由于每时隙中的大量码片,数据块长度 N 也很大。在[8] 中,作者发现,就TD-CDMA 参数 (在 N=60 的情况下)而言, Block-Fourier 算法的效率大约是Cholesky算法的2倍。而Block-Levinson, Block-Schur 算法 等后三者的效率非常相近 (其中Block-Schur 是三者中计算开销最高的)。 然而,当 N 减少时 (仍保持较大的 W) ,他们发现所有4种算法的计算效率非常相近。在[10] 中,作者发现,对于 TD-CDMA 而言, Fourier-Block 算法的效率明显高于Block-Fourier 算法, 且是目前已知的所有算法中最有效的。
然而,我们发现,对于 TD-SCDMA而言, Block-Fourier 和 Fourier-Block 算法的效率非常相近,并且比Block-Levinson,或 Block-Schur 算法的效率明显高很多。就乘法运算而言,Fourier-Block 算法也比Cholesky 算法的计算开销小。但是,如果考虑到其它浮点运算, Cholesky 算法具有最低的计算复杂度。
在 Table 0‑2 和 Table 0‑3 中,从乘法、除法、开平方根3种运算方面比较所有5种算法的浮点操作次数。 对于所完成的JD 处理,分别考虑了单天线和双天线用户终端2种情况, 以及一个时隙有10个码分用户的最恶劣的情况。与上一节相同,我们假设一次实数乘法等于一次浮点运算,一次实数除法需要6次浮点运算,一次实数平方根运算需要10次浮点运算。
我们采用[12]中的程序complexity.m 计算Block-Levinson, Block-Schur和 Block-Fourier 算法的浮点操作次数,Fourier-Block 算法的浮点操作次数在 0 中给出, Cholesky 算法的浮点操作次数在Table 0‑1中给出。
在比较的4种算法中,选用了近似的参数,以获得近似于理想的比特误码率性能。在仿真结果中,我们将会发现,对于Cholesky 算法,为获得近似于理想的TD-SCDMA比特误码率性能,复制下标必须取2 。对于这一点, [9]的作者发现在TD-CDMA 中也存在这种情况。对于其它4种算法,我们假设,在TD-CDMA 中可以给出近似于理想的比特误码率性能的近似参数,在TD-SCDMA 中也可以给出近似于理想的比特误码率性能。
从 Table 0‑2 和 Table 0‑3 可以看出,当给出近似于理想的比特误码率性能时,Cholesky 算法 (复制下标等于 2) 的计算开销最小,远远优于 Block-Levinson 和 Block-Schur 算法,略优于 Fourier 算法。当 M 等于 1时, Cholesky 算法优于其它4种算法中最优的Block-Fourier (16,2,3) 算法, 二者的浮点运算次数分别是139.8K 和 141.4K 。当 M 等于 2时, Cholesky 算法优于其它4种算法中最优的 Fourier-Block 算法,二者的浮点运算次数分别是207.2K 和 215.5K 。即使1.6K 到 8.3K 的浮点运算次数的差别可以近似认为没有差别, Cholesky 算法仍然是最优的, 因为它比Fourier 更直接。2种 Fourier 算法仍要求使用 Cholesky 因式分解,因为在这2种技术中Fourier 变换无法使相关矩阵对角化。
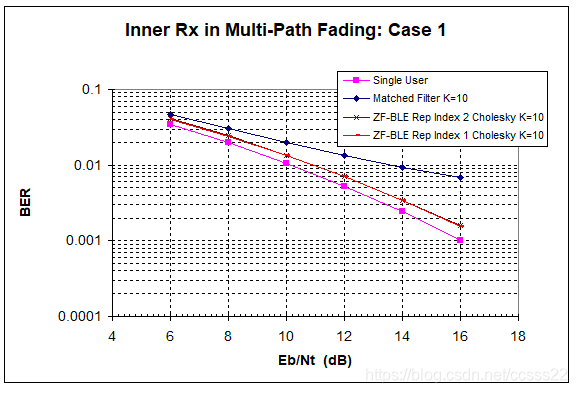
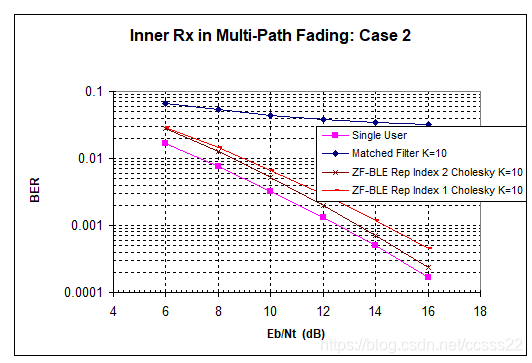
在只有一个用户的情况下,不存在多用户的用户间干扰, 因而单用户情况的结果也表示在一个时隙存在多个码分用户的情况下,多用户检测器可达到的最佳性能。 我们在仿真结果中,证明了在单用户情况下,匹配滤波器和ZF-BLE 检测器给出相同的性能,即是上述图中标记成“单用户”( “Single User”)的曲线。匹配滤波器等价于RAKE接收机。
为验证多用户检测器的性能,我们研究分析了一个时隙存在10个码分用户的最极端的情况。
对于衰落情况1,匹配滤波器在多用户情况下给出非常优异的性能,这是因为此时衰落信道中只有一条主传播路径 (第二主传播路径为接收机提供的功率比第一主传播路径整整低了10 dB)。 因而,对于情况1,路径传输损耗的作用,掩盖了用户间扩频码正交性的作用。
并且,事实上,对于情况2和3,我们可以看出匹配滤波器的性能很差,对消除用户间干扰根本没有任何作用– 请记住此时没有前向功控方法可用以使BER低于 1%。 对于cdmaOne,扩频因子是 64, 因而RAKE 接收机可以很好地消除多径干扰。而在 TD-SCDMA中,由于扩频因子较小,最大是 16, 此时仅使用RAKE 接收机是不够的,此时均衡变得非常重要。
在本文第3节中,我们采用具有近似因式分解,复制下标为1和2的 Cholesky 算法, 求解ZF-BLE 矩阵方程。 我们在 Figure 0‑1, Figure 0‑2和 Figure 0‑3中说明了使用复制下标2 的近似方法对BER 性能的影响。 研究结果表明,使用上述近似算法与使用准确的Cholesky 因式分解在求解ZF-BLE 矩阵方程上达到的性能没有区别。
无论是对于3种衰落情况中的哪一种,准确的 ZF-BLE 曲线都与上述图中给出的,标记为 “ZF-BLE Rep Index 2 Cholesky K=10” 曲线(该曲线使用的是复制下标为 2 的近似算法)相同。因而,我们没有在图中给出准确的 ZF-BLE 曲线,
如果采用复制下标1, 近似的Cholesky 算法相对于准确的求解算法会有一定的误差。在衰落情况1中,这种误差是0,但在衰落情况2中,随着SNR的增加,这种误差将随之增加, 当BER是 0.1% 时,误差是1dB。
对于我们研究分析的上述各种情况中,准确的ZF-BLE检测器的多用户性能非常接近单用户的理论极限。 对于衰落情况1,2和3 , BER 是 1% 时的误差分别是0.8,1.2和 2.2 dB。 如果在仿真模型中加入前向功控和信道编解码,将可以与标准的性能相比较[4]。