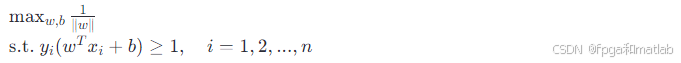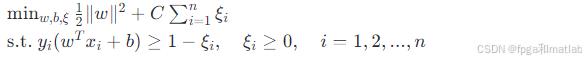目录
支持向量机(Support Vector Machine, SVM)是一种广泛应用于分类和回归任务的监督学习模型,尤其以其在高维空间中的强大分类能力而著称。其基本思想是通过构建一个最大间隔超平面来划分不同类别的数据,从而达到分类的目的。
SVM方法是20世纪90年代初Vapnik等人根据统计学习理论提出的一种新的机器学习方法,它以结构风险最小化原则为理论基础,通过适当地选择函数子集及该子集中的判别函数,使学习机器的实际风险达到最小,保证了通过有限训练样本得到的小误差分类器,对独立测试集的测试误差仍然较小。
支持向量机的基本思想是:首先,在线性可分情况下,在原空间寻找两类样本的最优分类超平面。在线性不可分的情况下,加入了松弛变量进行分析,通过使用非线性映射将低维输入空间的样本映射到高维属性空间使其变为线性情况,从而使得在高维属性空间采用线性算法对样本的非线性进行分析成为可能,并在该特征空间中寻找最优分类超平面。其次,它通过使用结构风险最小化原理在属性空间构建最优分类超平面,使得分类器得到全局最优,并在整个样本空间的期望风险以某个概率满足一定上界。
其突出的优点表现在:(1)基于统计学习理论中结构风险最小化原则和VC维理论,具有良好的泛化能力,即由有限的训练样本得到的小的误差能够保证使独立的测试集仍保持小的误差。(2)支持向量机的求解问题对应的是一个凸优化问题,因此局部最优解一定是全局最优解。(3)核函数的成功应用,将非线性问题转化为线性问题求解。(4)分类间隔的最大化,使得支持向量机算法具有较好的鲁棒性。由于SVM自身的突出优势,因此被越来越多的研究人员作为强有力的学习工具,以解决模式识别、回归估计等领域的难题。
1. 最大间隔分类
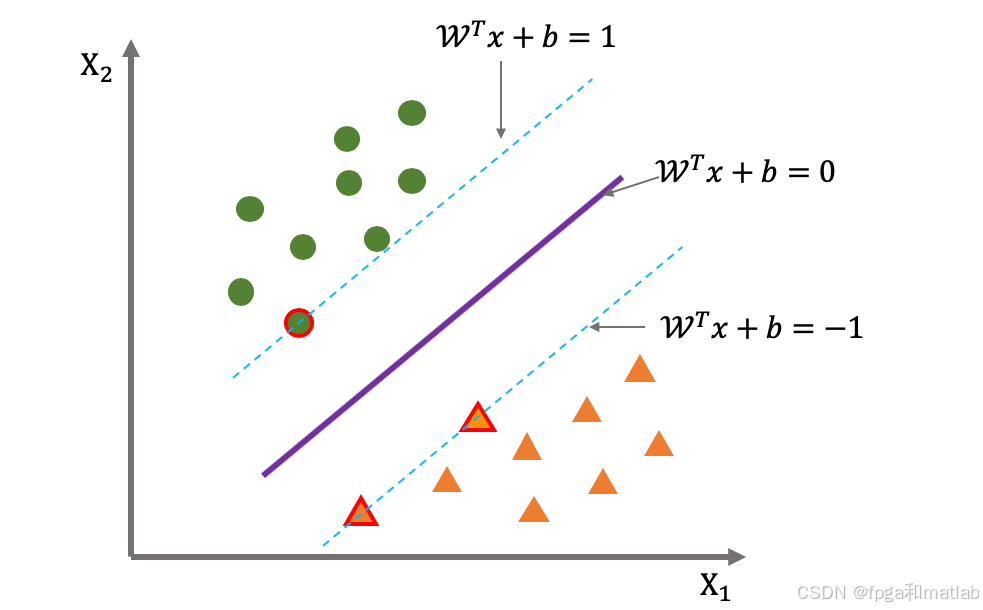
假设有两类样本集,分别记为C1和C2,我们的目标是找到一个超平面(在二维空间中是一条直线,在高维空间中是一个超平面)来完美地或尽可能好地将这两类样本分开。这个超平面定义为:
其中,w是超平面的法向量,x是样本点,b是偏置项。
SVM的核心思想是找到这样一个超平面,它不仅能够正确分类训练数据,而且使得距离超平面最近的样本点(支持向量)到超平面的距离最大化。这个最大间隔被称为“margin”,最大化间隔能够提高模型的泛化能力。
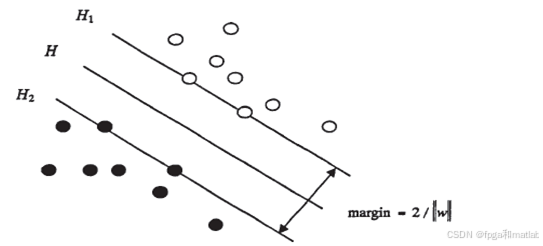
SVM是从线性可分情况下的最优分类面发展而来的,基本思想可用图1来说明。对于一维空间中的点,二维空间中的直线,三维空间中的平面,以及高维空间中的超平面,图中实心点和空心点代表两类样本,H为它们之间的分类超平面,H1,H2分别为过各类中离分类面最近的样本且平行于分类面的超平面,它们之间的距离△叫做分类间隔(margin)。
所谓最优分类面要求分类面不但能将两类正确分开,而且使分类间隔最大。将两类正确分开是为了保证训练错误率为0,也就是经验风险最小(为O)。使分类空隙最大实际上就是使推广性的界中的置信范围最小,从而使真实风险最小。推广到高维空间,最优分类线就成为最优分类面。
2. 函数间隔与几何间隔
3. 最优化问题
SVM的基本形式是求解一个凸优化问题,即寻找一个超平面使得所有样本的几何间隔最大化。转换为数学表达式为:
这个原始问题可以通过拉格朗日乘数法转化为对偶问题来解决,因为对偶问题通常更容易求解。
4. 对偶问题
5. 核函数
在处理非线性可分问题时,SVM通过引入核函数(Kernel Function)将输入数据从原始特征空间映射到一个高维特征空间,使得原本在低维空间中线性不可分的数据在高维空间中变得线性可分。常用的核函数有线性核、多项式核、高斯核(RBF)等。
6. 软间隔与正则化
实际应用中,数据往往存在噪声或异常点,导致完全线性分离不可行。为此,引入软间隔的概念,允许一些样本点位于超平面附近甚至错误分类,但需付出一定的代价。通过引入松弛变量ξi和正则化参数C,优化目标变为:
7.应用概述
SVM因其强大的泛化能力和对高维数据的有效处理,在众多领域有着广泛的应用,包括:
- 文本分类:利用词袋模型将文本转换为向量,然后使用SVM进行分类。
- 图像识别:通过提取图像的特征向量,SVM能够识别手写数字、人脸等。
- 生物信息学:在基因表达数据分类、蛋白质结构预测等方面发挥作用。
- 手写识别:将手写字符的像素特征向量作为输入,实现字符的自动识别。
- 金融风控:在信用评分、欺诈检测等场景中,SVM能有效区分正常交易与异常交易。