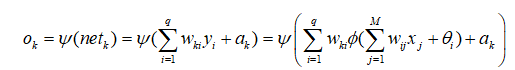欢迎订阅FPGA/MATLAB/Simulink系列教程
目录
1.使用软件和版本
matlab2022a/matlab2024b
2.BP神经网络理论概述
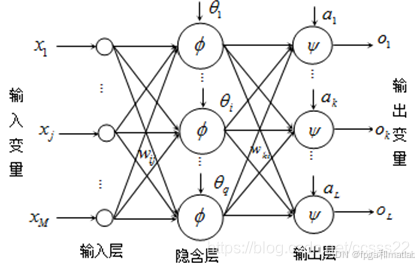
BP(Back Propagation)神经网络是一种按误差反向传播算法训练的多层前馈网络,它是目前应用最广泛的神经网络模型之一。其基本思想是信号前向传播,误差反向传播,通过不断调整网络的权值和阈值,使得网络的输出误差最小。BP神经网络的基本结构如下图所示:
从图的结构可知,BP神经网络主要由三个层次组成,包括BP神经网络的输入层,BP神经网络的隐含层以及BP神经网络的输出层。来自外部的各种信息通过BP神经网络的输入层传输进入到其隐含层进行网络运算处理,并通过输出层输出得到最终的处理结果。当BP神经网络的输出层输出结果和其预先设置的输入值的误差较大的时候,则进入BP神经网络的反向传播阶段,并进行网络权值的更新,直到输出结果和期望结果误差满足一定条件为止。
信号的前向传播过程的主要步骤如下:
第一、神经网络隐含层的第i个节点的输入变量neti:

第二、神经网络隐含层的第i个节点的输出变量yi:
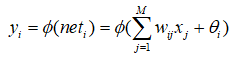
第三、神经网络输出层的第k个节点的输入变量netk:
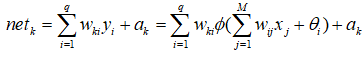
第四、神经网络输出层第k个节点的输出变量ok:
3.BP神经网络的MATLAB编程实现
在matlab中,我们将使用feedforwardnet函数来构建BP神经网络。其使用方法如下:
net = feedforwardnet(hiddenSizes,trainFcn)
返回前馈神经网络,其隐藏层大小为hiddenSizes,训练函数由trainFcn指定。
前馈网络由一系列层组成。第一层有来自网络输入的连接。每个后续层都有来自上一个层的连接。最终层产生网络的输出。
3.1 构建单输入-单输出的BP神经网络
我们编写如下的MATLAB程序:
clc;
clear;
close all;
warning off;
%100个样本,每个样本有5个输入特征和1个输出值
Num = 100; % 样本数量
Ni = 1; % 输入维度
No = 1; % 输出维度
X = rand(Ni, Num)+[1:Num]/10; % 输入数据,大小为 Ni x Num
T = sin([1:Num]/10); % 目标输出数据,大小为 No x Num
% 创建BP神经网络
% 隐藏层神经元数量设为10
Nhidden = 10;
net = feedforwardnet(Nhidden);
% 设置训练参数
net.trainParam.epochs = 1000; % 最大迭代次数
net.trainParam.lr = 0.01; % 学习率
net.trainParam.goal = 1e-5; % 目标误差
% 训练神经网络
[net, tr] = train(net, X, T);
% 使用训练好的网络进行预测
Y = net(X);
% 计算预测误差
error = T - Y;
mse = mean(error.^2); % 均方误差
fprintf('均方误差: %.6f\n', mse);
figure;
plot(T,'r','LineWidth',2);
hold on
plot(Y,'b-o');
legend('真实数据','预测数据');
% 绘制训练过程中的误差曲线
figure;
plot(tr.perf,'-r>',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.9,0.9,0.0]);
xlabel('迭代次数');
ylabel('均方误差');
title('训练过程中的均方误差变化');
grid on;
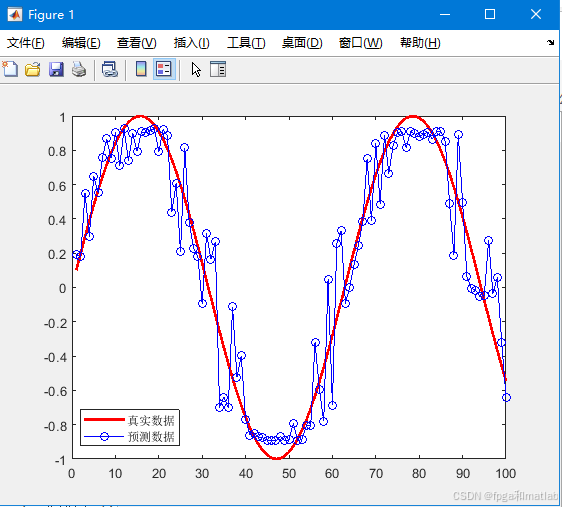
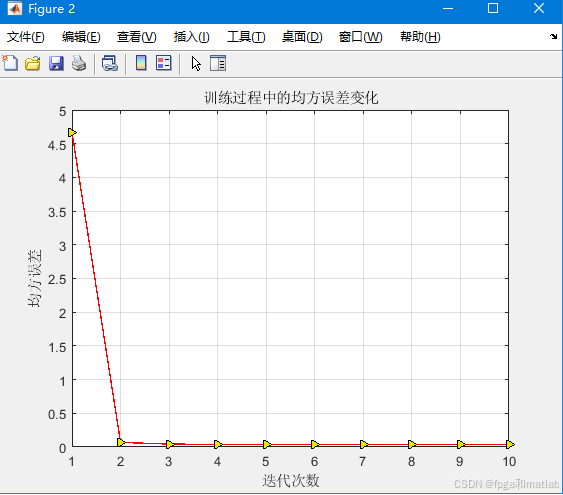
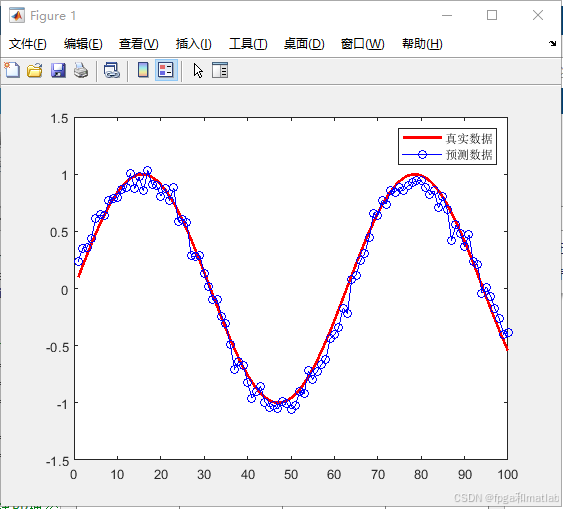
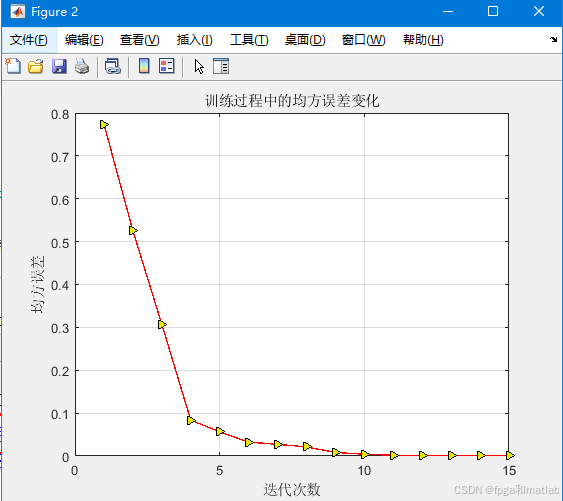
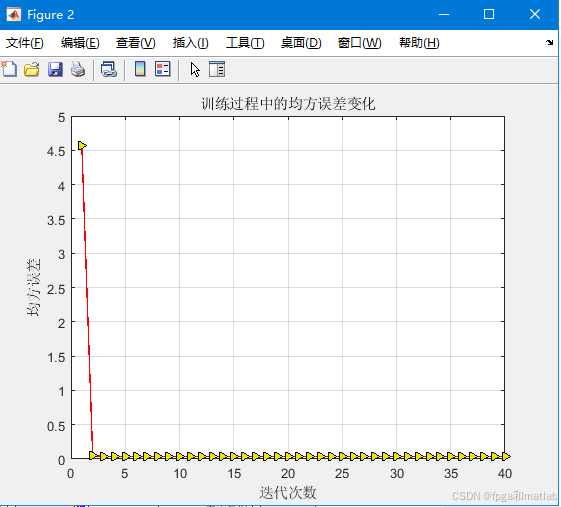
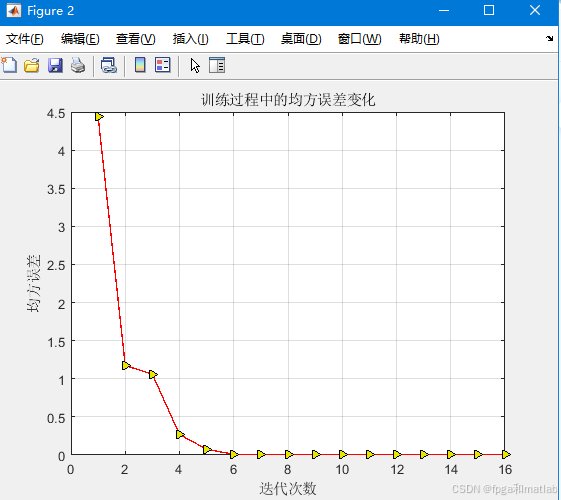
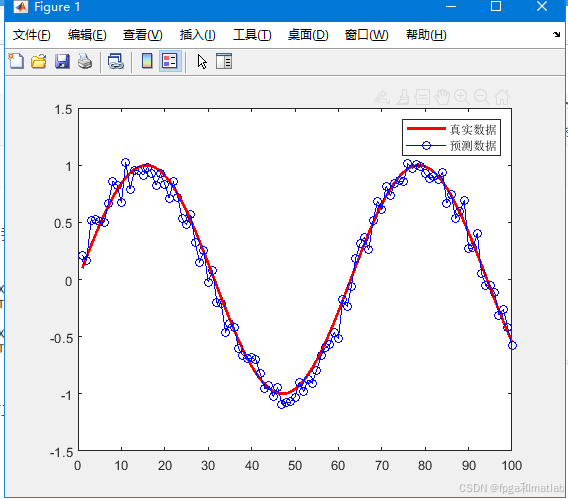
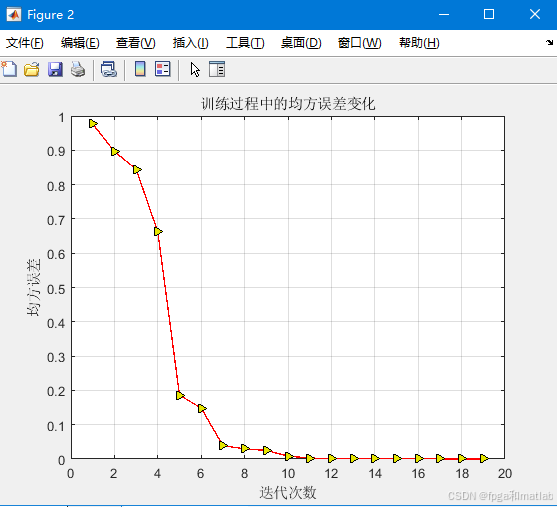
运行上述MATLAB程序,我们可以得到如下的仿真结果:
可以看到,通过BP神经网络,可以得到一个和真实数据接近的预测数据。
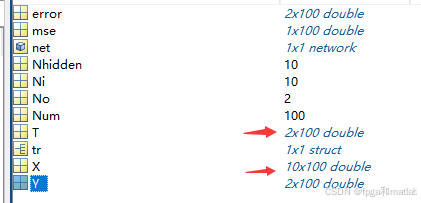
如果这里您需要替换自己的数据,则可以查看上述程序中如下变量:
其中X是输入,其维度是1*N,T为输出,其维度是1*N,直接替换X和T就可以了。
3.2 构建多输入-单输出的BP神经网络
我们将3.1小节中的程序中:
将Ni这个输入维度修改为大于1即可,比如我们改为10,然后运行程序,得到如下结果:
对比3.1的结论可知,输入维度越大,BP神经网络的预测输出越精确。
如果要替换数据,替换X和T即可。
其中X是输入,其维度是10*N,T为输出,其维度是1*N,直接替换X和T就可以了。
3.3 构建单输入-多输出的BP神经网络
我们将3.1小节中的程序中:
改为如下:
%100个样本,每个样本有5个输入特征和1个输出值
Num = 100; % 样本数量
Ni = 1; % 输入维度
No = 2; % 输出维度
X = rand(Ni, Num)+[1:Num]/10; % 输入数据,大小为 Ni x Num
T = [sin([1:Num]/10);cos([1:Num]/10)]; % 目标输出数据,大小为 No x Num
注意,这里输出我们以2为例子,所以输出训练样本T,为一个2*N维度的数据。
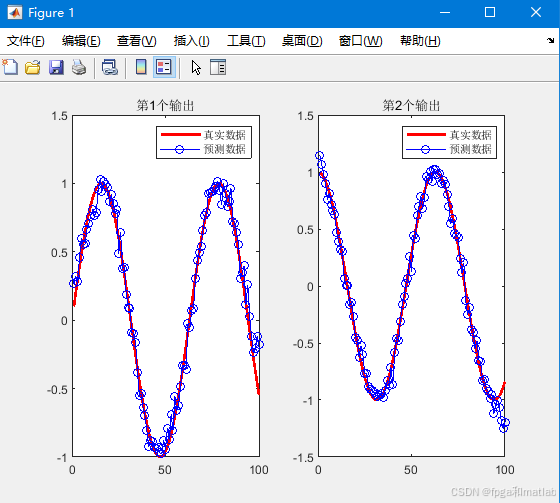
运行程序,得到如下结果:
如果要替换数据,替换X和T即可。
其中X是输入,其维度是1*N,T为输出,其维度是2*N,直接替换X和T就可以了。
3.4 构建多输入-多输出的BP神经网络
我们将3.1小节中的程序中:
改为如下:
%100个样本,每个样本有5个输入特征和1个输出值
Num = 100; % 样本数量
Ni = 10; % 输入维度
No = 2; % 输出维度
X = rand(Ni, Num)+[1:Num]/10; % 输入数据,大小为 Ni x Num
T = [sin([1:Num]/10);cos([1:Num]/10)]; % 目标输出数据,大小为 No x Num
注意,这里输出我们以2为例子,所以输出训练样本T,为一个2*N维度的数据。
运行程序,得到如下结果:
如果要替换数据,替换X和T即可。
其中X是输入,其维度是10*N,T为输出,其维度是2*N,直接替换X和T就可以了。
3.5 隐含层对BP神经网络性能的影响分析
我们按3.1的程序为基准,修改程序,编写一个不同隐含层大小的BP神经网络预测误差计算程序,matlab程序如下:
clc;
clear;
close all;
warning off;
idx=0;
for ii = [1,5,10,15,20,25]
idx=idx+1;
for jj=1:10
[ii,jj]
%100个样本,每个样本有5个输入特征和1个输出值
Num = 100; % 样本数量
Ni = 5; % 输入维度
No = 1; % 输出维度
X = rand(Ni, Num)+[1:Num]/10; % 输入数据,大小为 Ni x Num
T = sin([1:Num]/10); % 目标输出数据,大小为 No x Num
% 创建BP神经网络
% 隐藏层神经元数量设为ii
Nhidden = ii;
net = feedforwardnet(Nhidden);
% 设置训练参数
net.trainParam.epochs = 1000; % 最大迭代次数
net.trainParam.lr = 0.01; % 学习率
net.trainParam.goal = 1e-5; % 目标误差
% 训练神经网络
[net, tr] = train(net, X, T);
% 使用训练好的网络进行预测
Y = net(X);
% 计算预测误差
error = T - Y;
mse2(idx,jj) = mean(error.^2); % 均方误差
if ii == 1 & jj==1
figure;
plot(T,'r','LineWidth',2);
hold on
plot(Y,'b-o');
legend('真实数据','预测数据');
title('隐含层数=1');
end
if ii == 5 & jj==1
figure;
plot(T,'r','LineWidth',2);
hold on
plot(Y,'b-o');
legend('真实数据','预测数据');
title('隐含层数=5');
end
if ii == 15 & jj==1
figure;
plot(T,'r','LineWidth',2);
hold on
plot(Y,'b-o');
legend('真实数据','预测数据');
title('隐含层数=15');
end
if ii == 25 & jj==1
figure;
plot(T,'r','LineWidth',2);
hold on
plot(Y,'b-o');
legend('真实数据','预测数据');
title('隐含层数=25');
end
end
end
figure;
semilogy([1,5,10,15,20,25],mean(mse2,2),'-r>',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.9,0.9,0.0]);
xlabel('隐含层数');
ylabel('BP网络预测误差');
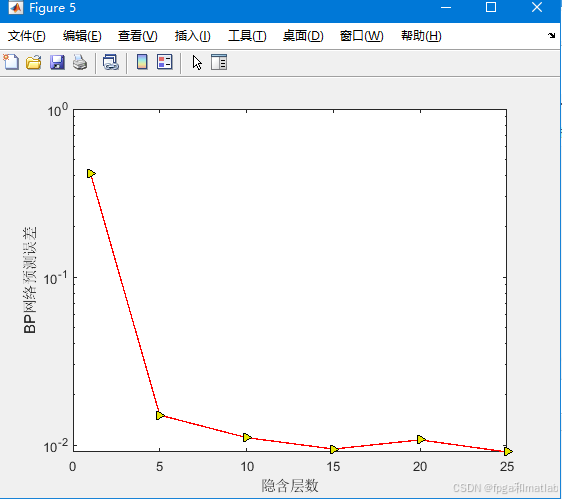
运行上述程序,可以得到如下的结论:
其误差曲线如下:
可以看到,随着隐含层数量的增加,BP神经网络的预测误差逐渐下降,当隐含层数量大于10时,预测误差基本收敛,文档在10的-2次方左右。
4.BP神经网络的泛化
BP神经网络的泛化能力指的是模型在未见过的数据上的表现能力,即模型对新数据的适应和预测准确性。较强的泛化能力意味着模型不仅在训练数据上表现良好,还能准确地对新数据进行分类或预测,这是衡量神经网络性能的关键指标之一。
上述第三小节,我们使用的训练样本和测试样本均为X,这里,我们重新定义一组未见过的数据作为测试样本进行测试。修改程序,得到如下的MATLAB程序:
clc;
clear;
close all;
warning off;
%100个样本,每个样本有5个输入特征和1个输出值
Num = 100; % 样本数量
Ni = 10; % 输入维度
No = 1; % 输出维度
X = rand(Ni, Num)+[1:Num]/10; % 输入数据,大小为 Ni x Num
T = sin([1:Num]/10); % 目标输出数据,大小为 No x Num
X2 = rand(Ni, Num)+[1:Num]/10; % 输入数据,大小为 Ni x Num
T2 = sin([1:Num]/10); % 目标输出数据,大小为 No x Num
% 创建BP神经网络
% 隐藏层神经元数量设为10
Nhidden = 10;
net = feedforwardnet(Nhidden);
% 设置训练参数
net.trainParam.epochs = 1000; % 最大迭代次数
net.trainParam.lr = 0.01; % 学习率
net.trainParam.goal = 1e-5; % 目标误差
% 训练神经网络
[net, tr] = train(net, X, T);
% 使用训练好的网络进行预测
Y2 = net(X2);
% 计算预测误差
error = T2 - Y2;
mse = mean(error.^2); % 均方误差
fprintf('均方误差: %.6f\n', mse);
figure;
plot(T2,'r','LineWidth',2);
hold on
plot(Y2,'b-o');
legend('真实数据','预测数据');
% 绘制训练过程中的误差曲线
figure;
plot(tr.perf,'-r>',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.9,0.9,0.0]);
xlabel('迭代次数');
ylabel('均方误差');
title('训练过程中的均方误差变化');
grid on;
上述程序中,我们做的修改:
这里添加了第二组数据作为未知数据进行测试,测试结果如下:
可以看到,通过BP神经网络,基本上可以对未知的数据做测试。
5.视频操作步骤演示
如果上述操作有什么不熟悉的地方,也可以参考如下的视频教程完成课程学习。