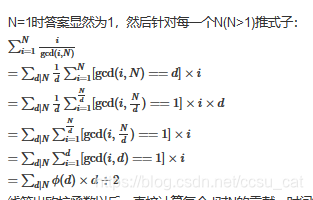今天出去玩了,所以比赛只打了一个小时.....
签到题,从第一个点开始找,每次都在合法的范围贪心去找一个最大的右端点,如果到了刚好不合法的点,那么答案++,合法范围变成之前的最大的右端点,然后继续找即可。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=1e5+10;
struct node
{
int l,r;
bool operator<(const node&t)const
{
if(l==t.l)return r>t.r;
return l<t.l;
}
}a[maxn];
int main()
{
int n,m,ans=1,mx,t;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
scanf("%d%d",&a[i].l,&a[i].r);
sort(a+1,a+1+m);
if(a[1].l>1)
puts("-1"),exit(0);
mx=t=a[1].r;
for(int i=2;i<=m;i++)
if(a[i].l<=t)
mx=max(mx,a[i].r);
else
{
if(a[i].l>mx+1)puts("-1"),exit(0);
if(a[i].l==t+1)
mx=max(mx,a[i].r);
t=mx;
ans++;
i--;
}
if(mx<n)puts("-1"),exit(0);
if(t!=n)ans++;
cout<<ans;
}签到题,快速幂结合快速乘即可,当然也可以用java大数快速幂(麻烦的解法)。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll mod;
ll mul(ll a,ll b)
{
ll res=0;
while(b)
{
if(b&1)res=(res+a)%mod;
a=(a+a)%mod;
b/=2;
}
return res;
}
ll ksm(ll a,ll b)
{
ll res=1;
while(b)
{
if(b&1)res=mul(res,a);
a=mul(a,a);
b/=2;
}
return res;
}
int main()
{
int T;
cin>>T;
while(T--)
{
ll a,b;
cin>>a>>b>>mod;
printf("%lld\n",ksm(a,b));
}
}设f[x]=x^n,不难发现f[ a*b ]=f[a]*f[b],因此我可以用线性筛求出所有素数x的f[ x ],其他所有合数的f[x]可通过两个因数相乘得到。D. 月月给华华出题
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=13000005,mod=1e9+7;
int vis[maxn],pri[maxn],cnt,n;
int d[maxn],ans;
int ksm(ll x,int y)
{
ll res=1;
while(y)
{
if(y&1)res=res*x%mod;
x=x*x%mod;
y/=2;
}
return res;
}
void init()
{
d[1]=1;
for(int i=2;i<=n;i++)
{
if(!vis[i])
pri[++cnt]=i,d[i]=ksm(i,n);
for(int j=1;j<=cnt&&pri[j]*i<=n;j++)
{
vis[pri[j]*i]=1;
d[pri[j]*i]=1ll*d[i]*d[pri[j]]%mod;
if(i%pri[j]==0)break;
}
}
for(int i=1;i<=n;i++)
ans^=d[i];
}
int main()
{
cin>>n;
init();
cout<<ans;
}
orz,数学差的我表示服气,公式推导到这后就可以直接枚举每个欧拉函数的贡献了。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=1e6+10;
int pri[maxn],vis[maxn],f[maxn],cnt,n;
ll ans[maxn];
void init()
{
f[1]=1;
for(int i=2;i<=n;i++)
{
if(!vis[i])
pri[++cnt]=i,f[i]=i-1;
for(int j=1;j<=cnt&&pri[j]*i<=n;j++)
{
vis[pri[j]*i]=1;
if(i%pri[j])
f[i*pri[j]]=f[i]*f[pri[j]];
else
{
f[i*pri[j]]=f[i]*pri[j];
break;
}
}
}
for(int i=1;i<=n;i++)
for(int j=i;j<=n;j+=i)
{
if(i==1)ans[j]+=1;
else ans[j]+=1ll*f[i]*i/2;
}
}
int main()
{
cin>>n;
init();
for(int i=1;i<=n;i++)
printf("%lld\n",ans[i]);
}
水题,二分即可。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=2e5+10;
int a[maxn],k,n;
int ok(int m)
{
ll res=0;
for(int i=1;i<=n;i++)
res+=a[i]/m;
if(res>=k)return 1;
return 0;
}
int main()
{
int l=1,r=1e9;
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
while(l<r)
{
int m=(l+r)/2;
if(ok(m))l=m+1;
else r=m;
}
if(!ok(l))l--;
cout<<l;
}我们设T=sqrt(n),每次操作1 D K,如果D>=T,那么我们就用树状数组暴力更新所有点x(x%D=0),如果D<T,那我们就跟新这个:a[D]+=K,查询区间[ l r ]的和,我们分别用树状数组求出对其的贡献,然后再求a数组对其的贡献即可。举个例子:ans+=n/i*a[i]。
#include<bits/stdc++.h>
#define low(x) x&-x
#define ll long long
using namespace std;
const int maxn=1e5+10;
ll c[maxn],a[maxn];
void up(int i,int v,int n)
{
for(;i<=n;i+=low(i))c[i]+=v;
}
ll qu(int i)
{
ll res=0;
for(;i;i-=low(i))res+=c[i];
return res;
}
int n,k,x,d,tp,T;
ll gao(int m)
{
ll res=qu(m);
int N=min(m,T);
for(int i=1;i<=N;i++)
res+=1ll*m/i*a[i];
return res;
}
int main()
{
scanf("%d%d",&n,&k);
T=(int)sqrt(1.0*n*2);
while(k--)
{
scanf("%d%d%d",&tp,&d,&x);
if(tp==1)
{
if(d>=T)
for(int i=d;i<=n;i+=d)up(i,x,n);
else a[d]+=x;
}
else
printf("%lld\n",gao(x)-gao(d-1));
}
}水题,就是求gcd(a,b),简单证明:我们都知道gcd是这样实现的:gcd(a,b)=gcd(b,a%b)=gcd(b,a-b),那么gcd(fn,fn-1)=gcd(fn-1,fn-2)=...
gcd(a,b)。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=2e5+10;
int main()
{
ll a,b,c;
cin>>a>>b>>c;
cout<<__gcd(a,b);
}这个题应该是最难的,我们先离线一下把整棵树给建出来,记录其dfs序,接下来再按顺序进行操作,如果操作2 i a,那我们就把i子树所有节点都+a,你可能有疑问,万一 i 子树有一个节点目前还没出现会有问题,好我们先不管这个继续其他操作你就明白了,假设操作 3 i,我们直接查询 i 的dfs序点的值即可,假设操作1 i,代表节点 i 插入一个儿子 x,如果之前 x 的祖先有进行过区间的加法,那么x子树每个节点权值都是错误的,这时我们就把x子树全部清0即可解决上面的问题。
#include<bits/stdc++.h>
#define low(x) x&-x
using namespace std;
const int maxn=4e5+10;
int c[maxn],cnt,sz[maxn],id[maxn];
void up(int i,int v)
{
for(;i<=cnt;i+=low(i))c[i]+=v;
}
int qu(int i)
{
int res=0;
for(;i;i-=low(i))res+=c[i];
return res;
}
struct node
{
int a,b,c;
}a[maxn];
vector<int>G[maxn];
void dfs(int u,int fa)
{
sz[u]=1;
id[u]=++cnt;
for(int i=0;i<G[u].size();i++)
{
int v=G[u][i];
if(v==fa)continue;
dfs(v,u);
sz[u]+=sz[v];
}
}
int main()
{
int m,n=0,res=0;
scanf("%d",&m);
for(int i=1;i<=m;i++)
{
scanf("%d%d",&a[i].a,&a[i].b);
if(a[i].a==1)
{
n++;
G[a[i].b].push_back(n);
G[n].push_back(a[i].b);
}
if(a[i].a==2)scanf("%d",&a[i].c);
}
dfs(0,-1);
for(int i=1;i<=m;i++)
if(a[i].a==1)
{
res++;
int x=qu(id[res]);
up(id[res],-x);
up(id[res]+sz[res],x);
}
else if(a[i].a==2)
{
up(id[a[i].b],a[i].c);
up(id[a[i].b]+sz[a[i].b],-a[i].c);
}
else printf("%d\n",qu(id[a[i].b]));
}裸的求无向图的桥,水题。
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
vector<int>G[maxn];
int cnt,res,low[maxn],dfn[maxn];
void dfs(int u,int fa)
{
dfn[u]=low[u]=++cnt;
for(int i=0;i<G[u].size();i++)
{
int v=G[u][i];
if(v==fa)continue;
if(!dfn[v])
{
dfs(v,u);
low[u]=min(low[u],low[v]);
if(low[v]>dfn[u])
res++;
}
else
low[u]=min(low[u],dfn[v]);
}
}
int main()
{
int n,m,u,v;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
scanf("%d%d",&u,&v);
G[u].push_back(v);
G[v].push_back(u);
}
dfs(1,0);
printf("%d\n",m-res);
}我们设a[ i ][ j ]表示原串第 j 个字母 a+'i' 出现的位置,那么我们如何判断abc是原串的子序列呢,先二分找到第一个a出现的位置x,接下来从[ x , n ]二分找到第一个b出现的位置pos,更新x=pos,接下来找 c 同理,如果什么时候找不到了就是No,否则Yes。
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+10;
char s[maxn];
int a[26][maxn],b[26];
int main()
{
int n,m;
scanf("%s",s+1);
for(int i=1;s[i];i++)
{
int x=s[i]-'a';
b[x]++;
a[x][b[x]]=i;
}
scanf("%d",&m);
while(m--)
{
scanf("%s",s+1);
int l=1,flag=1;
for(int i=1;s[i];i++)
{
int x=s[i]-'a';
if(a[x][b[x]]<l)
{
flag=0;
break;
}
int cur=lower_bound(a[x]+1,a[x]+b[x]+1,l)-a[x];
if(a[x][cur]<l)cur++;
l=a[x][cur]+1;
}
if(flag)printf("Yes\n");
else printf("No\n");
}
}