K近邻算法（K-Nearest Neighbors，简称KNN）是一种基于实例的学习方法，主要用于分类和回归问题。它的工作原理非常直观，核心思想是：如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别，那么该样本也属于这个类别，并具有这个类别上样本的特性。

以下是KNN算法的基本步骤：

1. 选择K值：首先，你需要确定一个合适的K值，即考虑最近的邻居数量。K值的选择对结果有很大影响，太小可能会受到噪声的影响，太大可能无法对数据进行准确建模。

2. 计算距离：对于给定的测试样本，计算其与训练集中的每个样本之间的距离。常用的距离度量有欧氏距离、曼哈顿距离等。

3. 找到K个最近邻：从训练集中找出距离测试样本最近的K个样本。

4. 决策规则：对于分类问题，通常采用多数表决法，即测试样本被分配到K个最近邻中出现次数最多的类别；对于回归问题，则可能是这K个样本目标值的平均值或加权平均值。

KNN算法的优点包括简单易理解、不需要训练过程（所有的“学习”都在预测阶段进行）、可以处理多分类问题以及非线性数据。然而，它的缺点也很明显，如计算量大（特别是当数据集很大时），且需要大量的内存来存储整个训练数据集；此外，K值的选择和距离度量方式对结果影响较大，需要适当调整。

KNN算法在很多领域都有应用，如文本分类、推荐系统、图像识别等。

在Mindspore中也可以使用K-means进行图像分类：

1.数据处理：

%matplotlib inline
import os
import csv
import numpy as np
import matplotlib.pyplot as plt

import mindspore as ms
from mindspore import nn, ops

ms.set_context(device_target="CPU")

with open('wine.data') as csv_file:
    data = list(csv.reader(csv_file, delimiter=','))
print(data[56:62]+data[130:133])

X = np.array([[float(x) for x in s[1:]] for s in data[:178]], np.float32)
Y = np.array([s[0] for s in data[:178]], np.int32)

attrs = ['Alcohol', 'Malic acid', 'Ash', 'Alcalinity of ash', 'Magnesium', 'Total phenols',
         'Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins', 'Color intensity', 'Hue',
         'OD280/OD315 of diluted wines', 'Proline']
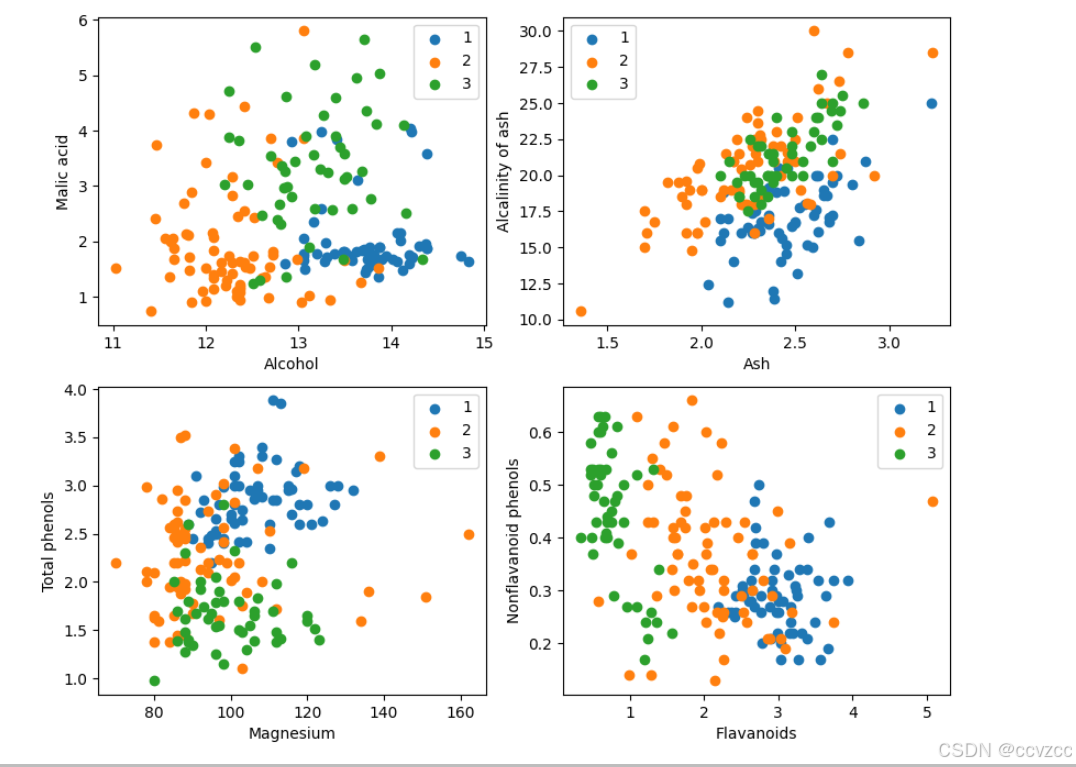
plt.figure(figsize=(10, 8))
for i in range(0, 4):
    plt.subplot(2, 2, i+1)
    a1, a2 = 2 * i, 2 * i + 1
    plt.scatter(X[:59, a1], X[:59, a2], label='1')
    plt.scatter(X[59:130, a1], X[59:130, a2], label='2')
    plt.scatter(X[130:, a1], X[130:, a2], label='3')
    plt.xlabel(attrs[a1])
    plt.ylabel(attrs[a2])
    plt.legend()
plt.show()

2.划分训练集：

train_idx = np.random.choice(178, 128, replace=False)
test_idx = np.array(list(set(range(178)) - set(train_idx)))
X_train, Y_train = X[train_idx], Y[train_idx]
X_test, Y_test = X[test_idx], Y[test_idx]

3.模型构建

class KnnNet(nn.Cell):
    def __init__(self, k):
        super(KnnNet, self).__init__()
        self.k = k

    def construct(self, x, X_train):
        #平铺输入x以匹配X_train中的样本数
        x_tile = ops.tile(x, (128, 1))
        square_diff = ops.square(x_tile - X_train)
        square_dist = ops.sum(square_diff, 1)
        dist = ops.sqrt(square_dist)
        #-dist表示值越大，样本就越接近
        values, indices = ops.topk(-dist, self.k)
        return indices

def knn(knn_net, x, X_train, Y_train):
    x, X_train = ms.Tensor(x), ms.Tensor(X_train)
    indices = knn_net(x, X_train)
    topk_cls = [0]*len(indices.asnumpy())
    for idx in indices.asnumpy():
        topk_cls[Y_train[idx]] += 1
    cls = np.argmax(topk_cls)
    return cls

acc = 0
knn_net = KnnNet(5)
for x, y in zip(X_test, Y_test):
    pred = knn(knn_net, x, X_train, Y_train)
    acc += (pred == y)
    print('label: %d, prediction: %s' % (y, pred))
print('Validation accuracy is %f' % (acc/len(Y_test)))