three.js中的矩阵变换(模型视图投影变换)

文章目录

1. 概述
2. 基本变换
3. 着色器变换
- 3.1. 代码
- 3.2. 解析
4. 其他

1. 概述

我在《WebGL简易教程(五)：图形变换(模型、视图、投影变换)》这篇博文里详细讲解了OpenGL\WebGL关于绘制场景的图形变换过程，并推导了相应的模型变换矩阵、视图变换矩阵以及投影变换矩阵。这里我就通过three.js这个图形引擎，验证一下其推导是否正确，顺便学习下three.js是如何进行图形变换的。

2. 基本变换

2.1. 矩阵运算

three.js已经提供了向量类和矩阵类，定义并且查看一个4阶矩阵类：

var m = new THREE.Matrix4();
m.set(11, 12, 13, 14,
    21, 22, 23, 24,
    31, 32, 33, 34,
    41, 42, 43, 44);
console.log(m);

输出结果：
imglink1

说明THREE.Matrix4内部是列主序存储的，而我们理论描述的矩阵都为行主序。

2.2. 模型变换矩阵

在场景中新建一个平面：

// create the ground plane
var planeGeometry = new THREE.PlaneGeometry(60, 20);
var planeMaterial = new THREE.MeshBasicMaterial({
    color: 0xAAAAAA
});
var plane = new THREE.Mesh(planeGeometry, planeMaterial);

// add the plane to the scene
scene.add(plane);

three.js中场景节点的基类都是Object3D，Object3D包含了3种矩阵对象：

Object3D.matrix: 相对于其父对象的局部模型变换矩阵。
Object3D.matrixWorld: 对象的全局模型变换矩阵。如果对象没有父对象，则与Object3D.matrix相同。
Object3D.modelViewMatrix: 表示对象相对于相机坐标系的变换。也就是matrixWorld左乘相机的matrixWorldInverse。

2.2.1. 平移矩阵

平移这个mesh：

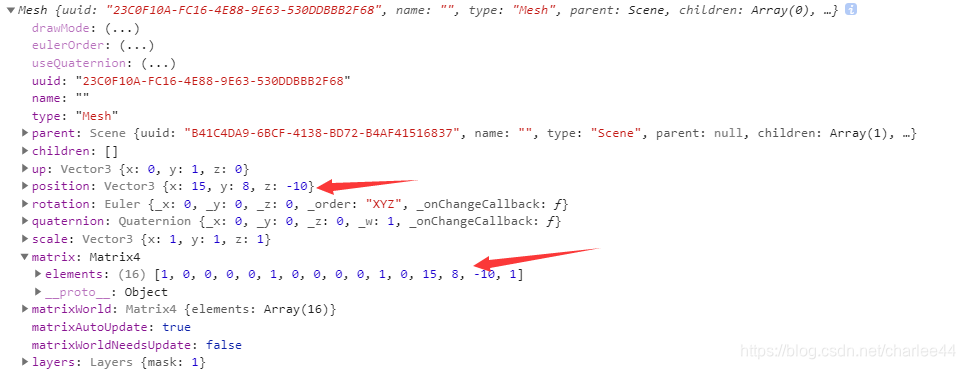
plane.position.set(15, 8, -10);

根据推导得到平移矩阵为：
$\left[ \begin{matrix} 1 & 0 & 0 & Tx\\ 0 & 1 & 0 & Ty\\ 0 & 0 & 1 & Tz\\ 0 & 0 & 0 & 1 \end{matrix} \right]$
输出这个Mesh：
imglink2

2.2.2. 旋转矩阵

2.2.2.1. 绕X轴旋转矩阵

绕X轴旋转：

plane.rotation.x = THREE.Math.degToRad(30);

对应的旋转矩阵：
$\left[ \begin{matrix} 1 & 0 & 0 & 0\\ 0 & cosβ & -sinβ & 0\\ 0 & sinβ & cosβ & 0\\ 0 & 0 & 0 & 1 \end{matrix} \right]$

输出信息：
imglink3

2.2.2.2. 绕Y轴旋转矩阵

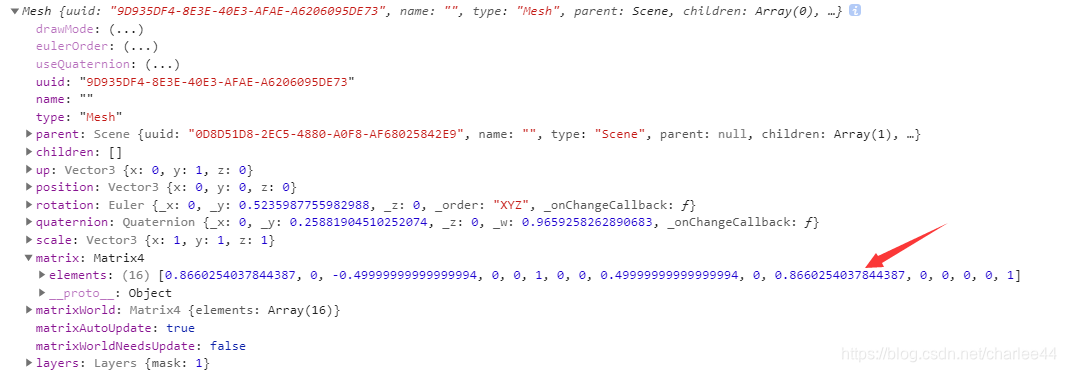
绕Y轴旋转：

plane.rotation.y = THREE.Math.degToRad(30);

对应的旋转矩阵：
$\left[ \begin{matrix} cosβ & 0 & sinβ & 0\\ 0 & 1 & 0 & 0\\ -sinβ & 0 & cosβ & 0\\ 0 & 0 & 0 & 1 \end{matrix} \right]$

输出信息：
imglink4

2.2.2.3. 绕Z轴旋转矩阵

绕Z轴旋转：

plane.rotation.z = THREE.Math.degToRad(30);

对应的旋转矩阵：
$\left[ \begin{matrix} cosβ & -sinβ & 0 & 0\\ sinβ & cosβ & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{matrix} \right]$

输出信息：
imglink5

2.3. 投影变换矩阵

在场景中新建一个Camera：

var camera = new THREE.PerspectiveCamera(45, window.innerWidth / window.innerHeight, 0.1, 1000);

这里创建了一个透视投影的相机，一般建立的都是对称的透视投影，推导的透视投影矩阵为：
$\left[ \begin{matrix} \frac{1}{aspect*tan⁡(\frac{fovy}{2})} & 0 & 0 & 0 \\ 0 & \frac{1}{tan⁡(\frac{fovy}{2})} & 0 & 0 \\ 0 & 0 & \frac{f+n}{n-f} & \frac{2fn}{n-f} \\ 0 & 0 & -1 & 0 \\ \end{matrix} \right]$

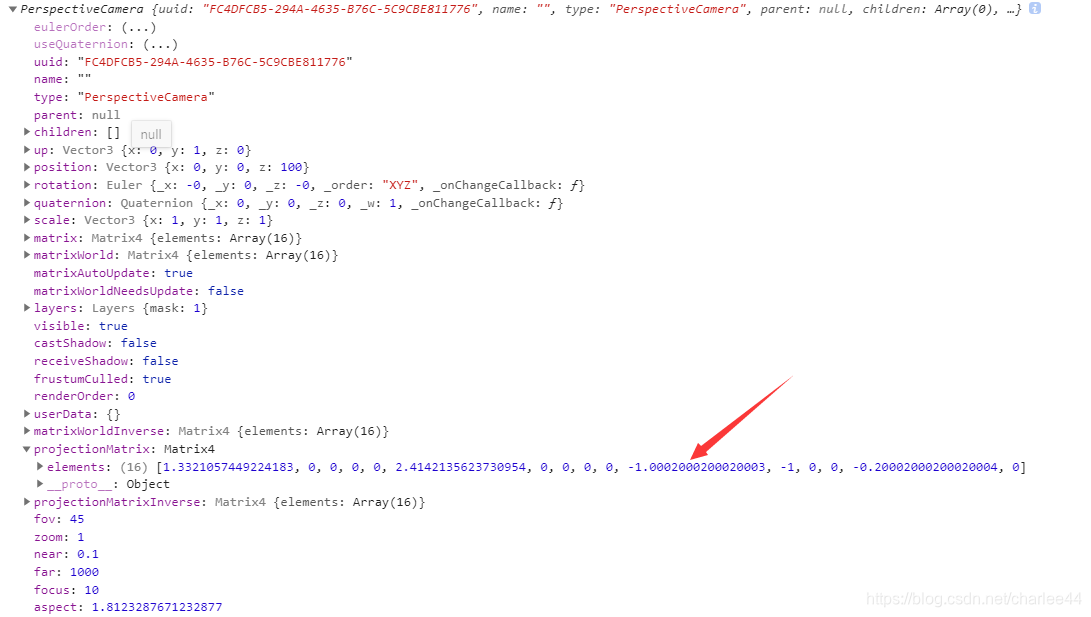
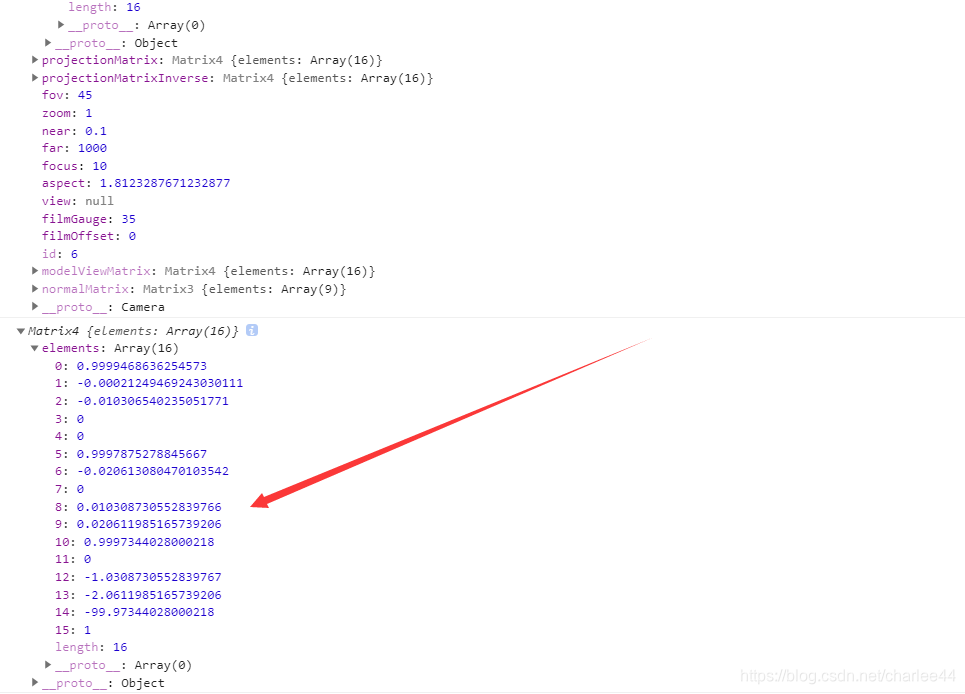
为了验证其推导是否正确，输出这个camera，查看projectionMatrix，也就是透视投影矩阵：
imglink6

2.4. 视图变换矩阵

通过Camera可以设置视图矩阵：

camera.position.set(0, 0, 100);   //相机的位置
camera.up.set(0, 1, 0);         //相机以哪个方向为上方
camera.lookAt(new THREE.Vector3(1, 2, 3));          //相机看向哪个坐标

根据《WebGL简易教程(五)：图形变换(模型、视图、投影变换)》中的描述，可以通过three.js的矩阵运算来推导其视图矩阵：

var eye = new THREE.Vector3(0, 0, 100);
var up = new THREE.Vector3(0, 1, 0);
var at = new THREE.Vector3(1, 2, 3);

var N = new THREE.Vector3();
N.subVectors(eye, at); 
N.normalize();
var U = new THREE.Vector3();
U.crossVectors(up, N);
U.normalize();
var V = new THREE.Vector3();
V.crossVectors(N, U);
V.normalize();

var R = new THREE.Matrix4();
R.set(U.x, U.y, U.z, 0,
    V.x, V.y, V.z, 0,
    N.x, N.y, N.z, 0,
    0, 0, 0, 1);  

var T = new THREE.Matrix4(); 
T.set(1, 0, 0, -eye.x,
    0, 1, 0, -eye.y,
    0, 0, 1, -eye.z,
    0, 0, 0, 1);  

var V = new THREE.Matrix4();
V.multiplyMatrices(R, T);   
console.log(V);

其推导公式如下：
$V=R^{-1} T^{-1}= \left[ \begin{matrix} Ux & Uy & Uz & 0 \\ Vx & Vy & Vz & 0 \\ Nx & Ny & Nz & 0 \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right] * \left[ \begin{matrix} 1 & 0 & 0 & -Tx \\ 0 & 1 & 0 & -Ty\\ 0 & 0 & 1 & -Tz\\ 0 & 0 & 0 & 1\\ \end{matrix} \right] = \left[ \begin{matrix} Ux & Uy & Uz & -U·T \\ Vx & Vy & Vz & -V·T \\ Nx & Ny & Nz & -N·T \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right]$

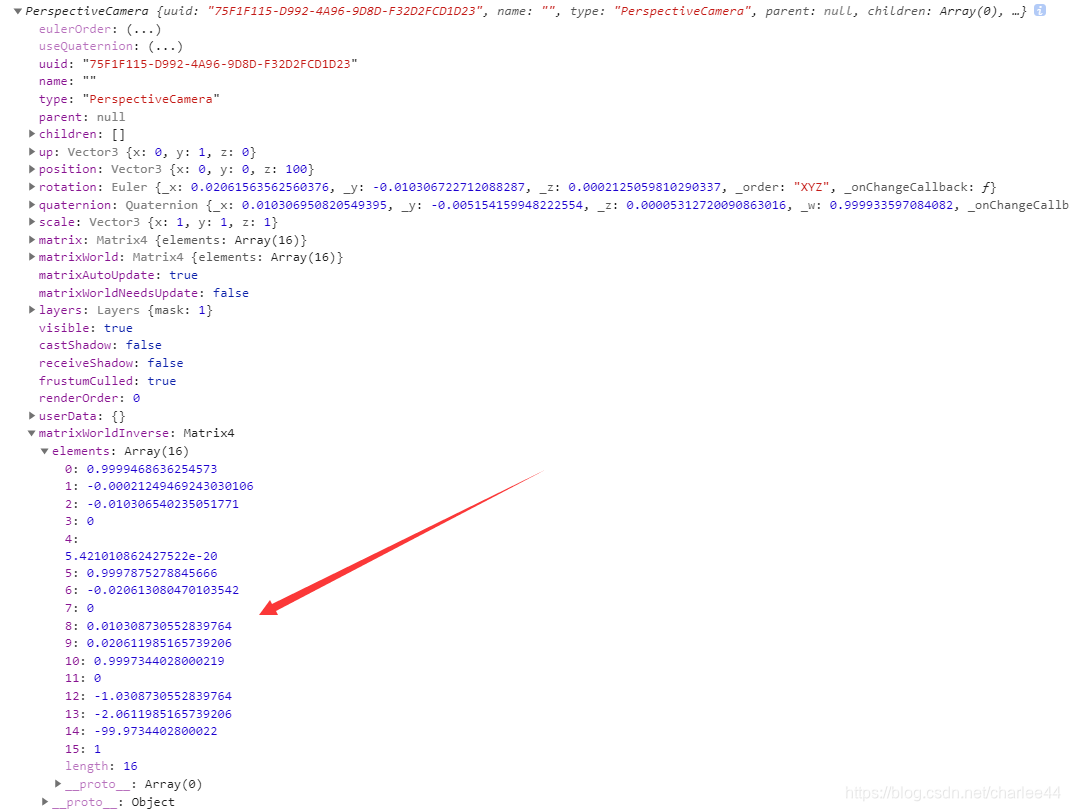
最后输出它们的矩阵值：
imglink7
imglink8

两者的计算结果基本时一致的。需要注意的是Camera中表达视图矩阵的成员变量是Camera.matrixWorldInverse。它的逻辑应该是视图矩阵与模型矩阵互为逆矩阵，模型矩阵也可以称为世界矩阵，那么世界矩阵的逆矩阵就是视图矩阵了。

3. 着色器变换

可以通过给着色器传值来验证计算的模型视图投影矩阵（以下称MVP矩阵）是否正确。对于一个任何事情都不做的着色器来说：

vertexShader: ` 
    void main() { 
        gl_Position = projectionMatrix * modelViewMatrix * vec4( position, 1.0 );      
    }`
,

fragmentShader: `       
    void main() {    
        gl_FragColor = vec4(0.556, 0.0, 0.0, 1.0)                   
    }`

projectionMatrix和modelViewMatrix分别是three.js中内置的投影矩阵和模型视图矩阵。那么可以做一个简单的验证工作，将计算得到的MVP矩阵传入到着色器中，代替这两个矩阵，如果最终得到的值是正确的，那么就说明计算的MVP矩阵是正确的。

3.1. 代码

实例代码如下：

<!DOCTYPE html>
<html>

<head>
    <title>Example 01.01 - Basic skeleton</title>
    <meta charset="UTF-8" />
    <script type="text/javascript" charset="UTF-8" src="../three/three.js"></script>
    <script type="text/javascript" charset="UTF-8" src="../three/controls/TrackballControls.js"></script>
    <script type="text/javascript" charset="UTF-8" src="../three/libs/stats.min.js"></script>
    <script type="text/javascript" charset="UTF-8" src="../three/libs/util.js"></script>
    <script type="text/javascript" src="MatrixDemo.js"></script>
    <link rel="stylesheet" href="../css/default.css">
</head>

<body>
    <!-- Div which will hold the Output -->
    <div id="webgl-output"></div>

    <!-- Javascript code that runs our Three.js examples -->
    <script type="text/javascript">
        (function () {
            // contains the code for the example
            init();
        })();
    </script>
</body>

</html>

'use strict';

THREE.StretchShader = {

    uniforms: {   
        "sw" : {type:'b', value : false},
        "mvpMatrix" : {type:'m4',value:new THREE.Matrix4()}    
    },

    // 
    vertexShader: `    
        uniform mat4 mvpMatrix;
        uniform bool sw;
        void main() { 
            if(sw) {
                gl_Position = mvpMatrix * vec4( position, 1.0 );  
            }else{
                gl_Position = projectionMatrix * modelViewMatrix * vec4( position, 1.0 ); 
            }       
        }`
    ,

    //
    fragmentShader: `   
        uniform bool sw; 
        void main() {    
            if(sw) {
                gl_FragColor = vec4(0.556, 0.0, 0.0, 1.0); 
            }else {
                gl_FragColor = vec4(0.556, 0.8945, 0.9296, 1.0); 
            }                    
        }`
};


function init() {
    //console.log("Using Three.js version: " + THREE.REVISION);   

    // create a scene, that will hold all our elements such as objects, cameras and lights.
    var scene = new THREE.Scene();

    // create a camera, which defines where we're looking at.
    var camera = new THREE.PerspectiveCamera(45, window.innerWidth / window.innerHeight, 0.1, 1000);

    // position and point the camera to the center of the scene
    camera.position.set(0, 0, 100);   //相机的位置
    camera.up.set(0, 1, 0);         //相机以哪个方向为上方
    camera.lookAt(new THREE.Vector3(1, 2, 3));          //相机看向哪个坐标
 
    // create a render and set the size
    var renderer = new THREE.WebGLRenderer();
    renderer.setClearColor(new THREE.Color(0x000000));
    renderer.setSize(window.innerWidth, window.innerHeight);

    // add the output of the renderer to the html element
    document.getElementById("webgl-output").appendChild(renderer.domElement);

    
    // create the ground plane
    var planeGeometry = new THREE.PlaneGeometry(60, 20);
    // var planeMaterial = new THREE.MeshBasicMaterial({
    //     color: 0xAAAAAA
    // });

    var planeMaterial = new THREE.ShaderMaterial({
        uniforms: THREE.StretchShader.uniforms,
        vertexShader: THREE.StretchShader.vertexShader,
        fragmentShader: THREE.StretchShader.fragmentShader
    });

    var plane = new THREE.Mesh(planeGeometry, planeMaterial);

    // add the plane to the scene
    scene.add(plane);

    // rotate and position the plane    
    plane.position.set(15, 8, -10);
    plane.rotation.x = THREE.Math.degToRad(30);
    plane.rotation.y = THREE.Math.degToRad(45);
    plane.rotation.z = THREE.Math.degToRad(60);
 
    render();
  
    var farmeCount = 0;
    function render() {    
        
        var mvpMatrix = new THREE.Matrix4(); 
        mvpMatrix.multiplyMatrices(camera.projectionMatrix, camera.matrixWorldInverse);    
        mvpMatrix.multiplyMatrices(mvpMatrix, plane.matrixWorld);   
        
        THREE.StretchShader.uniforms.mvpMatrix.value = mvpMatrix; 
        if(farmeCount % 60 === 0){
            THREE.StretchShader.uniforms.sw.value = !THREE.StretchShader.uniforms.sw.value;
        }          
        
        farmeCount = requestAnimationFrame(render);
        renderer.render(scene, camera);
    }
   
}

3.2. 解析

这段代码的意思是，给着色器传入了计算好的MVP矩阵变量mvpMatrix，以及一个开关变量sw。开关变量会每60帧变一次，如果为假，会使用内置的projectionMatrix和modelViewMatrix来计算顶点值，此时场景中的物体颜色会显示为蓝色；如果开关变量为真，则会使用传入的计算好的mvpMatrix计算顶点值，此时场景中的物体颜色会显示为红色。运行截图如下：
imglink9

可以看到场景中的物体的颜色在红色与蓝色之间来回切换，且物体位置没有任何变化，说明我们计算的MVP矩阵是正确的。

4. 其他

在使用JS的console.log()进行打印camera对象的时候，会发现如果不调用render()的话（或者单步调式），其内部的matrix相关的成员变量仍然是初始化的值，得不到想要的结果。而console.log()可以认为是异步的，调用render()之后，就可以得到正确的camera对象了。