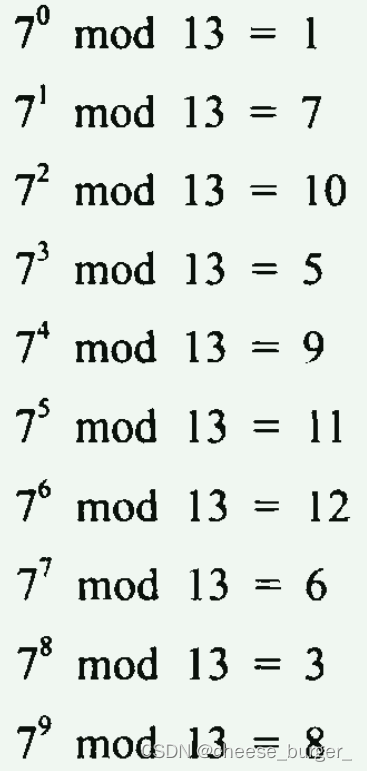$$用公钥加密，用私钥解密$$

一、投币寄物柜的使用方法

 首先，将物品放人寄物柜中。然后，投入硬币并拔出钥匙，就可以将寄物柜关闭了。关闭后的寄物柜，没有钥匙是无法打开的。
 只要有硬币，任何人都可以关闭寄物柜，但寄物柜一旦被关闭，再怎么投币也无法打开。打开寄物柜需要使用钥匙，而不是硬币。
 因此我们可以说，硬币 是关闭寄物柜的密钥，而 钥匙 则是打开寄物柜的密钥。

二、本章学习的内容

 在 对称密码 中，由于 加密和解密的密钥是 相同的，因此必须 向接收者 配送密钥。用于解密的密钥必须被配送给接收者，这一问题称为 密钥配送问题。
 如果使用 公钥密码，则无需向接收者配送用于解密的密钥，这样就解决了密钥配送问题。可以说公钥密码是密码学历史上最伟大的发明¹。

 本章中，我们将首先来探讨一下 密钥配送问题，然后再来讲解 公钥密码 是如何解决密钥配送问题的。最后，我们还将介绍一种最常用的公钥密码 —— RSA。

三、密钥配送问题

1、什么是密钥配送问题

 在现实世界中使用对称密码时，我们一定会遇到 密钥配送问题 (key distribution problem)。
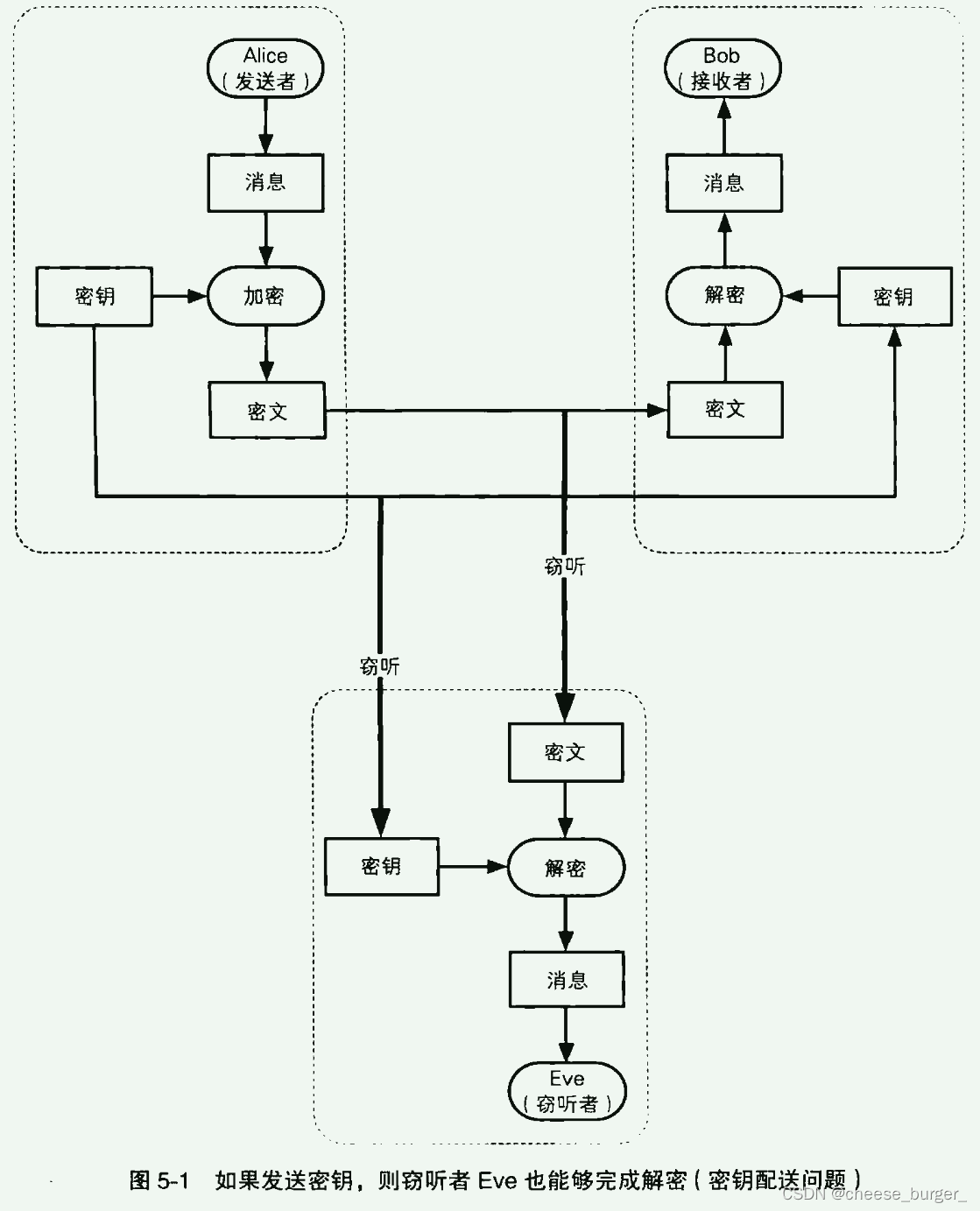
 假设 Alice 和 Bob 用过 对称加密 进行对话。Alice 不但要将 密文 发送给 Bob，还需要将 密钥 也发送给 Bob，这样 Bob 才能解密 密文 得到 明文。
 但是，如果同时发送密文和密钥，则 Eve 也能够同时拿到 密文和密钥 完成解密，图5-1。
 当然，如果窃听者 Eve 无法知道使用的是什么密码算法，那么即便得到了密文和密钥也是无法解密的。然而，密码算法本来就应该是以 公开 为前提的，隐蔽式安全性 是非常危险的。

 密钥必须要发送，但又不能发送，这就是对称密码的 密钥配送问题。

 解决密钥配送问题有如下几种方法：

1. 通过 事先共享密钥 来实现；
2. 通过 密钥分配中心 来解决；
3. 通过 Diffice-Hellman 来解决；
4. 通过 公钥密码 来结局。

2、事先共享密钥

 就是 事先 用 安全的方式 将密钥交给对方，这称为密钥的 事先共享。

 首先通过网络的方法事先将密钥给对方，和 同时发送密文和密钥 没有任何区别。最安全的永远是发送者自己，那就是发送者自己在现实世界中将密钥告诉接收者。这一方面受到了时间距离的限制，另一方面，如果接收者不只一个人，那么每个人都需要一个密钥，事情会变得更加麻烦。

3、密钥分配中心

 如果所有参与加密通信的人都需要 事先共享密钥，则 密钥的数量 会变得巨大，在这样的情况下，可以使用 密钥分配中心 (Key Distribution Center, KDC) 来解决密钥配送问题。
 当需要进行加密通信时，密钥分配中心 会生成一个通信密钥，每个人只要和密钥分配中心 事先共享密钥 就可以了。那么，现在 Alice 再向 Bob 发送加密邮件时，就需要进行以下步骤：

1. Alice 向 密钥分配中心 发出希望与 Bob 进行通信的请求；
2. 密钥分配中心 通过 伪随机数生成器 生成一个 会话密钥，这个密钥是供 Alice 与 Bob 在本次通信中使用的 临时密钥；
3. 密钥分配中心 从数据库中取出 Alice的密钥 和 Bob的密钥；
4. 密钥分配中心 用 Alice的密钥 对 会话密钥 进行加密，并发送给 Alice；
5. 密钥分配中心 用 Bob的密钥 对 会话密钥 进行加密，并发送给 Bob；
6. Alice 对来自密钥分配中心的 会话密钥 (已使用Alice的密钥加密) 进行解密，得到 会话密钥；
7. Alice 用 会话密钥 对 邮件 进行 加密，并将邮件发送给 Bob；
8. Bob 对来自密钥分配中心的 会话密钥 (已使用Bob的密钥加密) 进行解密，得到 会话密钥；
9. Bob 用 会话密钥 对来自 Alice 的 密文 进行解密；
10. Alice 和 Bob 删除 会话密钥。

 然后来看看缺点：过于依赖中心，只要中心出现任何问题，便会导致所有人都无法相互通信，比如：数据太多导致瘫痪、中心受到攻击 … …

4、Diffie-Hellman 密钥交换

 这里的 交换，并不是指东西坏了需要换一个，而是指发送者和接收者之间相互传递信息的意思。
 在 Diffie-Hellman密钥交换中，进行加密通信的双方需要交换 一些信息，而这些信息 即便被窃听者 Eve 窃听到也没有问题。
 根据所交换的信息，双方可以 各自生成 相同的密钥，而 窃听者Eve 却 无法 生成相同的密钥。Eve 虽然能够窃听到双方所交换的信息，但却 无法根据这些信息生成和双方 相同的密钥。

 关于 Diffie-Hellman 密钥交换，将在 第11章 详细探讨。

5、公钥密码

 公钥密码 中，加密密钥 和 解密密钥 却是 不同的。只要拥有加密密钥，任何人都可以进行加密，但没有解密密钥是无法解密的。
 因此，公钥密码的一个重要性质，就是 只有拥有 解密密钥 的人才能够进行解密。
 接收者 事先将 加密密钥 发送给 发送者，加密密钥 即便被窃听者获取也没有问题。发送者 使用 加密密钥 对通信内容进行加密，并发送给 接收者，而只有拥有解密密钥的人 (即接收者本人) 才能够进行解密。

四、公钥密码

1、什么是公钥密码

 公钥密码中，密钥分为 加密密钥 和 解密密钥 两种。

• 加密密钥，一般是公开的，因此也称为 公钥 public key。
• 解密密钥，是绝对不能公开的，因此也称为 私钥 private key。

 可以发现加密密钥和解密密钥之间的一些特点：

1. 发送者 只需要 加密密钥；
2. 接收者 只需要 解密密钥；
3. 解密密钥 不可以被窃听者听到；
4. 加密密钥 被窃听者听到也没有什么问题。

 公钥和私钥是一一对应的，一对公钥和私钥 统称为 密钥对 key pair。由公钥进行加密的密文，必须使用 与该公钥配对的 私钥 才能够解密。
 密钥对中的两个密钥之间具有非常密切的关系 —— 数学上的关系，因此公钥和私钥是不能分别单独生成的。
 公钥密码的使用者 (一般是消息的接收者) 需要生成一个包括公钥和私钥的 密钥对，其中公钥会被发送给别人，而私钥则仅供自己使用。由于 私钥 是由 接收者 一直保存在 本地的，所以不存在 密钥配送问题。

2、公钥的历史

略

3、公钥通信的流程

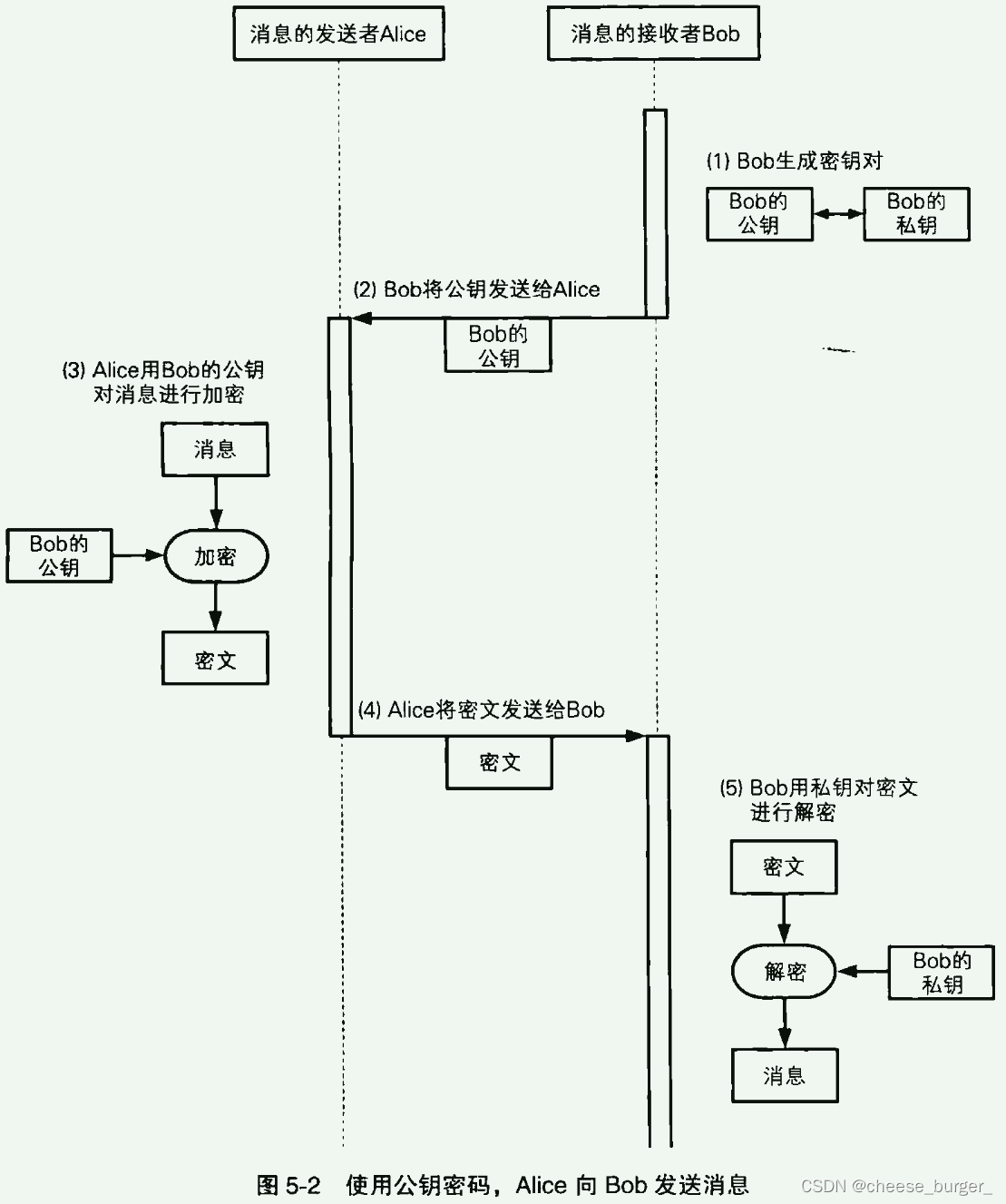
 基本过程上面已经说过了，即 接收者*将 公钥 (加密密钥) 发送给 发送者，发送者 用接收到的 公钥 对消息进行加密生成 密文，并将 密文 发送给 接收者。接收者 收到密文后用 私钥 (解密密钥) 将密文解密成明文，如图5-2 所示：
 其实可以观察到：Alice 和 Bob 之间传输的信息只有两个：

• Bob 的公钥
• 公钥加密的密文

就算被 Eve 全部窃听到了，也没关系，因为 Eve 没有 解密密钥。

4、公钥密码无法解决的问题

• 公钥认证问题：
   公钥密码解决了密钥配送问题，但这并不意味着它能够解决所有的问题，因为我们需要 判断所得到的公钥是否正确合法，这个问题被称为 公钥认证问题。关于这个问题，我们将在后面的章节中通过对 中间人攻击 的讲解来探讨。
• 处理速度较慢：
   此外，公钥密码还有一个问题就是，它的 处理速度 只有 对称密码的几百分之一。关于这个问题的解决方法，我们将在下一章中进行介绍。

五、时钟运算

 在讲解公钥密码的代表 RSA 之前，我们需要做一些数学方面的准备工作，即 时钟运算²，实际上就是 取余运算。

1、加法

$$(7+20)mod12=27mod12=3$$

2、减法

减法实际上就是加法
$$(5-3)mod12=(5-3+12)mod12=(5+9)mod12=2$$

3、乘法

$$(7\times 4)mod12=28mod12=4$$

4、除法

 除法也就可以看成是 乘法的逆运算。例如，在下面的算式中：
$$(7\times x)mod12=1$$想要知道 x 的值是多少，在时钟运算中就是 将 “向右转动 7 个刻度” 的操作重复几次指针会指向 1 呢?
 刚才上述式子的描述是 在mod12的世界中，7乘以几等于1，换句话就是 在mod12的世界中，1除以7等于几。在一般的整数世界中，1 除以7是除不尽的，但在以12为模的世界中却可以除尽。$$(7\times x)mod12=1\to (1÷7)mod12=x$$

 再来看看下面这个算式：
$$(x\times y)mod=1$$我们可以称 在mod12的世界里，x 和 y 是 互为 倒数 的关系。

 实际上，时钟运算中 “某个数是否存在倒数” 这个问题，与 公钥算法RSA 中 “一个公钥是否存在相对应的私钥” 这个问题是直接相关的。

 直接给结论：在 mod 12 的世界中，存在倒数的数，它们和 12 之间的 最大公约数 都是 1 (公约数只有1)。

5、乘方

6、对数

 乘方的逆运算称为对数，时钟运算中的对数称为 离散对数，例如：
$$7^{x}mod13=8$$来尝试以下暴力的方法：
 当数字很大时，求离散对数 非常困难，也非常耗时。能快速求出离散对数的算法到 现在还没有被发现。Diffie-Hellman密钥交换协议 (之前解决密钥配问题中有提到) 以及 ElGamal公钥算法 中就运用了离散对数。

六、RSA

1、什么是 RSA

 RSA 可以被用于 公钥密码 和 数字签名，关于数字签名我们将在 第9章 进行讲解。

2、RSA 加密

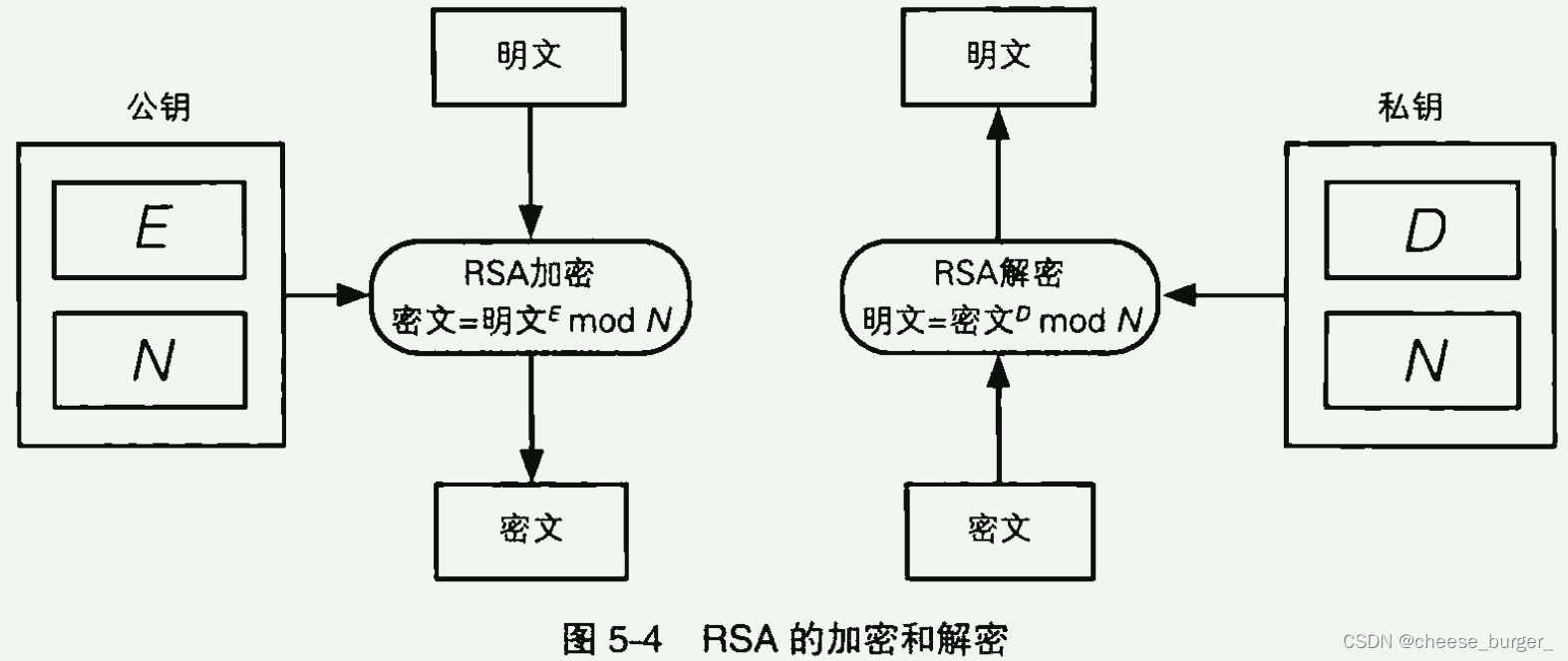
 在 RSA 中，明文、密钥、密文 都是 数字。RSA 的 加密过程 可以用下列公式来表达，这个公式很重要：
$$密文=明{文}^{E}modN(RSA加密)$$上述公式就是将明文加密的方法了，没错就是这么简单，只要知道 E 和 N，任何人都可以对明文进行加密，但是 E 和 N 并不是随便什么数都可以的，它们是需要经过严密计算的，这个稍后会说。
 E 和 N 两个数才组成了一个公钥，因此我们一般会写成 “公钥是 (E, N)” 或者 “公钥是 {E, N}” 这样的形式。

3、RSA 解密

 RSA 解密和加密一样可以用一个公式来表示：
$$明文=密{文}^{D}modN(RSA加密)$$D 和 N 的组合就是一个 私钥，所以也可以写成 私钥是 (D, N) 或 {D, N}。
 当然，D 也并不是随便什么数都可以的，作为解密密钥的 D，和数字 E 有着相当紧密的联系。

要加密的明文必须是小于 N 的数，这是因为：解密的时候需要 mod N，这是一定不会生成一个大于等于 N 的明文的。

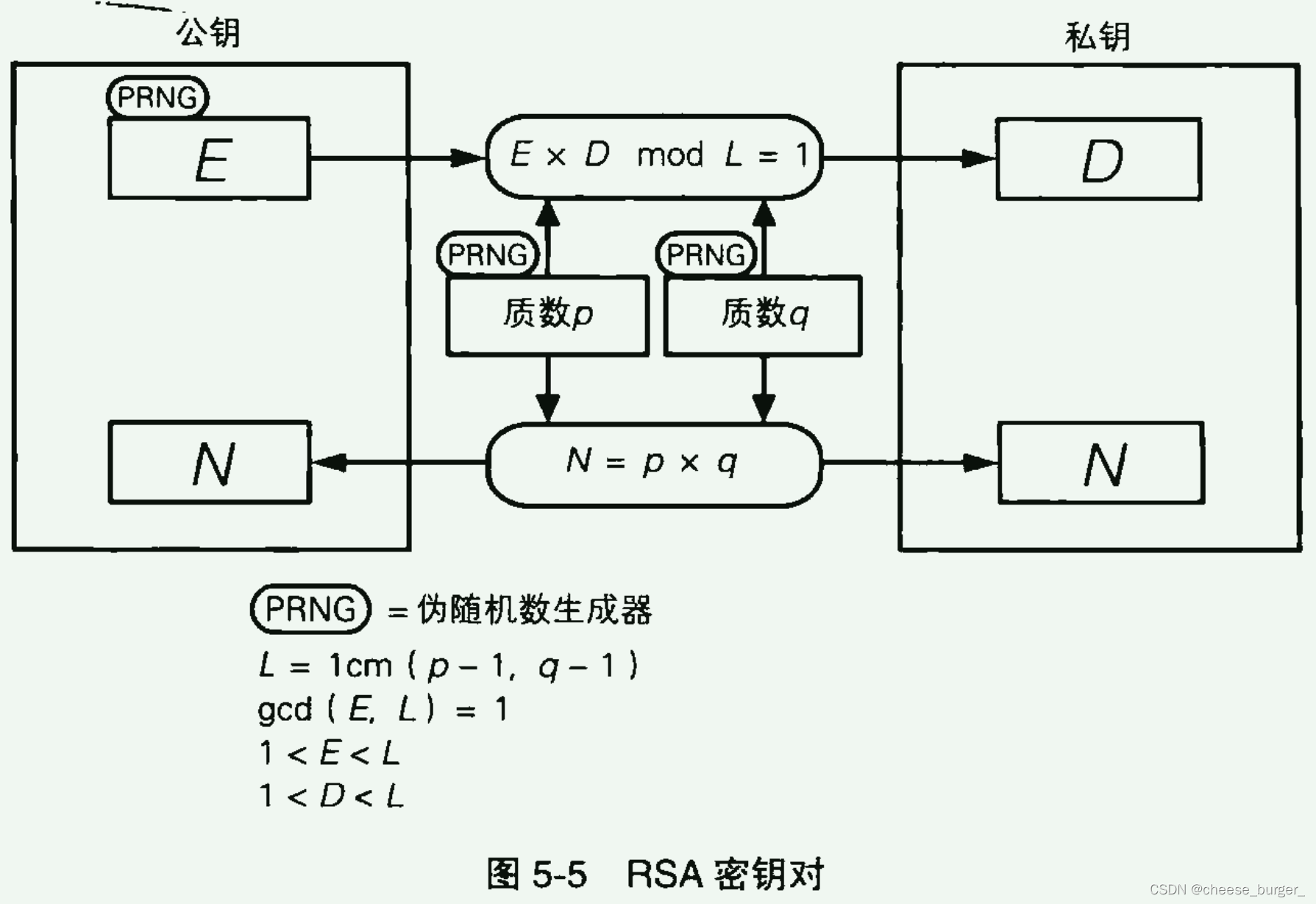
4、生成密钥对

 由于E 和 N 是公钥，D 和 N 是私钥，因此求 E、D、N 这三个数就是 生成密钥对。RSA 密钥对的生成步骤如下：

1. 求 N；
2. 求 L (L 是仅在生成密钥对的过程中使用的数)；
3. 求 E；
4. 求 D。

4.1、求 N

 先准备两个很大的质数 p 和 q，p 和 q 的大小要合适，太小会导致容易破译，太大会导致计算时间很长。
 假设现在需要一个 512bit 的质数，相当于 155位 的十进制数。通过一个 伪随机数生成器 随机生成一个 512bit 的数即可，如果该数不是质数，则再生成一个，直到生成了两个质数 p 和 q。

判断一个数是不是质数是通过数学方法实现的，包括 费马测试 和 米勒·拉宾测试 等。

 所需要的 N 就是：$N=p\times q$。至于为什么是两个质数相乘，这里就先省略了。

4.2、求 L

 L 是 p-1 和 q-1 的 最小公倍数。如果用 lcm(X,Y) 来表示 "X 和 Y 的最小公倍数”***==，则 L 可以写成下列形式：
$$L=lcm(p-1,q-1)$$

4.3、求 E

 E 是一个比 1 大、比 L 小的数。此外，E 和 L 的 最大公约数 (gcd) 必须为 1。如果用 gcd(X, Y) 来表示 X 和 Y 的最大公约数，则 E 和 L 之间存在下列关系：
$$1<E<L，gcd(E,L)=1$$要找出满足 gcd(E, L)=1 的数，还需要使用 伪随机数生成器。通过伪随机数生成器在 1 < E < L 的范围内生成 E 的候选数，然后再判断其是否满足 gcd(E, L) = 1 这个条件。求最大公约数可以使用欧几里得的辗转相除法。
 简单来说，之所以要加上 E 和 L 的最大公约数为 1 这个条件，是为了保证一定存在解密时
需要使用的数D。
 至此，加密所需要的 E 和 N 都已经求出来了。

4.4、求 D

 D 是由 E 计算出来的，D、E、L 之间必须具备下列关系。
$$1<D<L，E\times DmodL=1$$只要 D 满足上述条件，则通过 E 和 N 进行加密的密文，就可以通过 D 和 N 进行解密。
 $E\times DmodL=1$ 这样的公式在 时钟运算 中也出现过，且由 时钟运算 可知，要保证存在满足条件的 D，就需要保证 E 和 L 的最大公约数为 1。
 至此，解密所需要的 D 和 N 都已经求出来了。

七、对 RSA 的攻击

 RSA 的加密解密原理非常简单，但是作为密码算法，RSA 的机密性如何呢？即，密码破译者是不是也能够还原出明文呢？
 这个问题非常重要，我们先来整理一下密码破译者知道的以及不知道的信息。

• 破译者知道的信息：
  1. 密文：可以通过窃听来获取
  2. E 和 N：公钥是公开的信息，因此密码破译者知道 E 和 N
• 破译者不知道的信息：
  1. 明文：需要破译的内容
  2. D：私钥中至少不知道 D
  3. 其他：密码破译者不知道生成密钥对时所使用的 p、q、L

 接下来讨论一下破译 RSA 的方法。

1、通过密文来破获明文

 RSA 的加密过程为：
$$密文=明{文}^{E}modN$$ 由于密码破译者知道密文 E 和 N，如果没有 “mod N”，那这个问题就是求对数。但是加上 “mod N” 之后，问题便变成了 求离散对数 的问题，这是非常困难的，人类目前还没找到求离散对数的高效算法。

2、通过暴力破解来找出 D

 RSA 的解密过程为：
$$明文=密{文}^{D}modN$$ 只要能知道 D，就能对密文进行解密。那么此时就会想能不能暴力出 D 呢？
 现在，RSA 中所使用的 p 和 q 的长度都是 1024比特 以上，N 的长度为 2048比特 以上。由于 E 和 D 的长度可以和 N 差不多，因此要找出 D，就需要进行 2048比特 以上的暴力破解。要在这样的长度下用暴力破解找出 D 是极其困难的。

3、通过 E 和 N 求 D

 在计算 D 的过程中，关系式为：
$$E\times DmodL=1$$出现的数字是 L，而 $L=lcm(p-1,q-1)$，由于 p 和 q 是破译者所不知道的，所以也无法得到 L，进而无法得到 D。
 反之，如果破译者知道了 p 和 q，也就等价于知道了 D。
 虽然破译者不能直接得到 p 和 q，但是下面有一些想法，我们来讨论一下它们的可行性：

3.1、对 N 进行质因数分解

 $N=p\times q$，而且 N 是公开的，那么能不能由 N 求出 p 和 q呢？由于 p 和 q 都是质数，所以该问题就是 将 N 进行质因数分解。
 一旦发现了对大整数进行质因数分解的高效算法，RSA 就能够被破译。
 然而，现在我们还没有发现对 大整数进行质因数分解 的 高效算法，而且也尚未证明质因数分解是否真的是非常困难的问题，甚至也 不知道 是否存在一种分解质因数的简单方法。

3.2、通过推测 p 和 q 进行攻击

 由于 p 和 q 是通过 伪随机数生成器 产生的，如果伪随机数生成器的算法很差，密码破译者就有可能 推测出 p 和 q 因此使用能够被推测出来的随机数是非常危险的。

4、中间人攻击

 这种方法虽然不能破译 RSA，但却是一种 针对机密性 的有效攻击。

 所谓中间人攻击，就是 主动攻击者Mallory 混入发送者和接收者的中间，对发送者伪装成接收者，对接收者伪装成发送者 的攻击方式，在这里 Mallory 就是 “中间人”。

 上述过程可以反复多次，Bob 向 Alice 发送加密邮件时也可能受到同样的攻击，因此 Bob 即便要发邮件给 Alice 以询问她真正的想法，也会被 Mallory 随意篡改。

 这种攻击不仅针对 RSA，而是可以 针对任何公钥密码。在这个过程中，公钥密码并没有被破译，所有的密码算法也都正常工作并确保了机密性。
 然而，所谓的机密性并非在 Alice 和 Bob 之间，而是在 Alice 和 Mallory 之间，以及 Mallory 和 Bob之间成立的。

仅靠公钥密码本身，是无法防御中间人攻击的。
要防御中间人攻击，还需要一种手段来 确认所收到的公钥是否真的属于 Bob, 这种手段称为 认证。在这种情况下，我们可以使用公钥的证书。关于证书，我们会在 第10章 进行探讨。

5、选择密文攻击

 在研究密码算法的强度时，我们会假设 攻击者有能力获得一些关键信息。比如，一般我们都会假设攻击者已经知道我们所使用的密码算法，只是 不知道密钥 而已。

 在 选择密文攻击 (Chosen Ciphertext Attack) 中，我们假设攻击者可以使用这样一种服务，即 “发送任意数据，服务器都会将其当作密文来解密并返回解密的结果”，这种服务被称为 解密提示 (Decryption Oracle)。

 实际上，网络上很多服务器在收到格式不正确的数据时都会向通信对象返回错误消息，并提示 “这里的数据有问题"。然而，在使用密码进行通信的情况下，这种看似很贴心的设计却会让攻缶者有机可乘。
 攻击者可以向服务器反复发送自己生成的伪造密文，并通过分析服务器返冋的错误消息和响应时间获得一些关于密钥和明文的信息。

5.1、RSA-OAEP算法 (加了认证)

 接下来思考一下，如何改进 RSA 才能抵御密文攻击呢？只要我们在 解密时 能够判断 “密文是否是由 知道明文的人 通过 合法的方式 生成的” 就可以了。换句话说，也就是 对密文进行 “认证”。RSA-OAEP (Optimal Asymmetric Encryption Padding，最优非对称加密填充) 正是基于上述思路设计的一种 RSA 改良算法 (RFC2437)。

 RSA-OAEP 在 加密时 会在 明文前面 填充一些 认证信息，包括 明文的散列值 以及 一定数量的 0，然后再对填充后的明文 用 RSA 进行加密。

 在 RSA-OAEP 的 解密过程 中，如果在 RSA 解密后的 数据的开头 没有找到 正确的认证信息，则可以断定 “这段密文不是由知道明文的人生成的”，并返回一条 固定的错误消息 “ decryption error” (这里的重点是，不能将具体的错误内容告知发送者)。

可以看出 RSA-OAEP 就是在 RSA 加密之前对明文进行填充，并在解密后可以通过填充信息进行一些判断。

 这样一来，攻击者就无法通过 RSA-OAEP 的 解密提示 获得有用的信息，因此这一算法 能够抵御选择密文攻击。
 在 RSA-OAEP 的实际运用中，还会通过 随机数 使得 每次生成的密文 呈现 不同的排列方式，从而进一步提高安全性。

八、其他公钥密码

 RSA 是现在最为普及的一种公钥密码算法。现在介绍一些其他的公钥算法：ElGamal方式、Rabin方式、椭圆曲线密码。这些密码都可以被用于一般的加密和数字签名。

1、ElGamal方式

 RSA 利用了质因数分解的困难度，而 ElGamal方式 则利用了 ==mod N下求离散对数的困难度。
 ElGamal方式 有一个缺点，就是 经过加密的密文长度 会变为 明文 的 两倍。密码软件 GnuPG 中就支持这种方式。

2、Rabin方法

 Rabin方式 利用了 mod N下求平方根的困难度。上文中我们提到了破解 RSA 有可能不需要通过对大整数 N 进行质因数分解，而破译 Rabin方式 公钥密码的困难度与质因数分解则是相当的，这一点已经得到了证明。

3、椭圆曲线密码

 補圆曲线密码 (Elliptic Curve Cryptography, ECC) 是最近备受关注的一种公钥密码算法。它的特点是 所需的密钥长度比 RSA 短。
 椭圆曲线密码是通过 将 椭圆曲线 上的 特定点 进行 特殊的乘法运算 来实现的，它利用了这种 乘法运算的逆运算 非常困难 这一特性。关于椭圆曲线密码的详细内容，请参考附录。