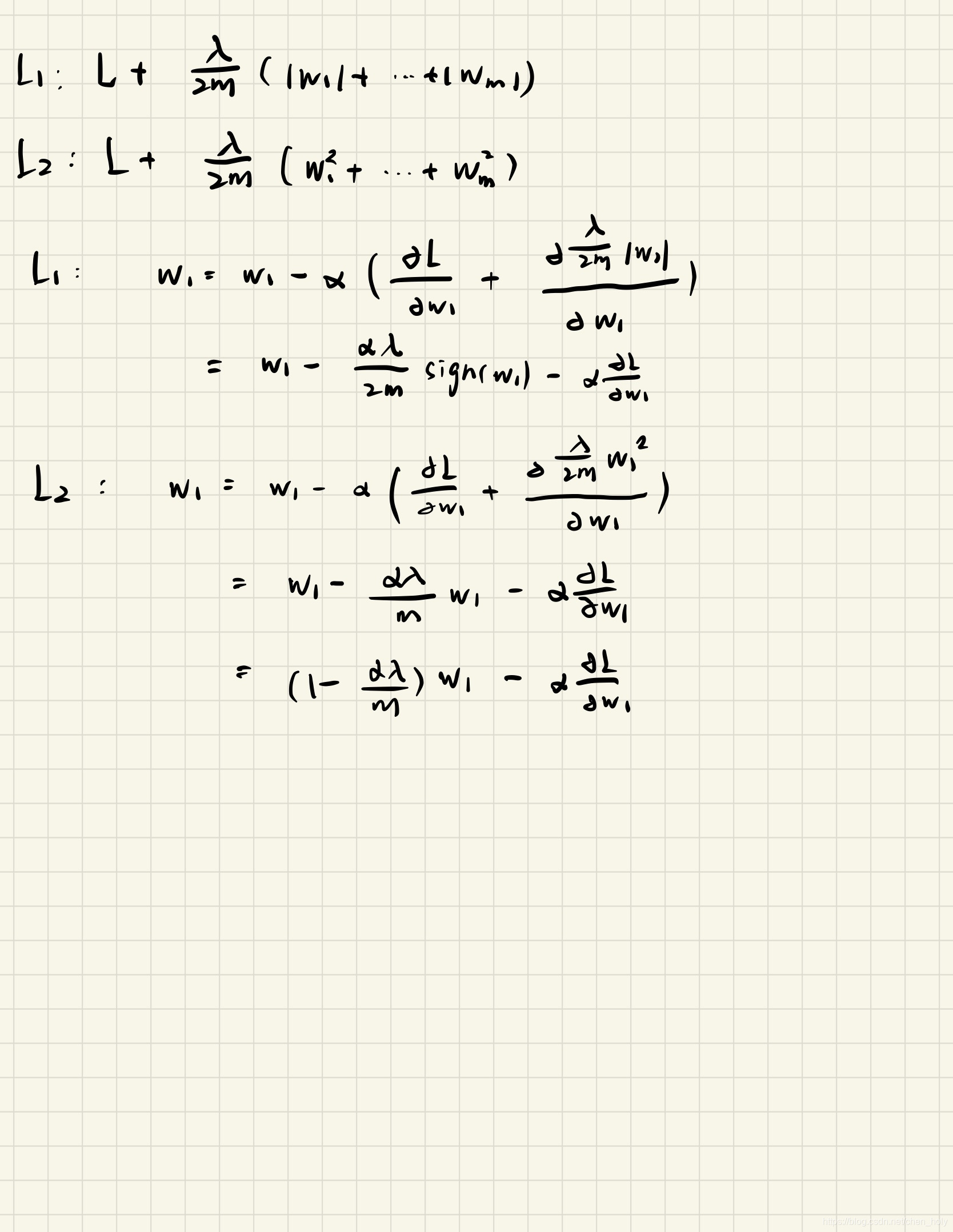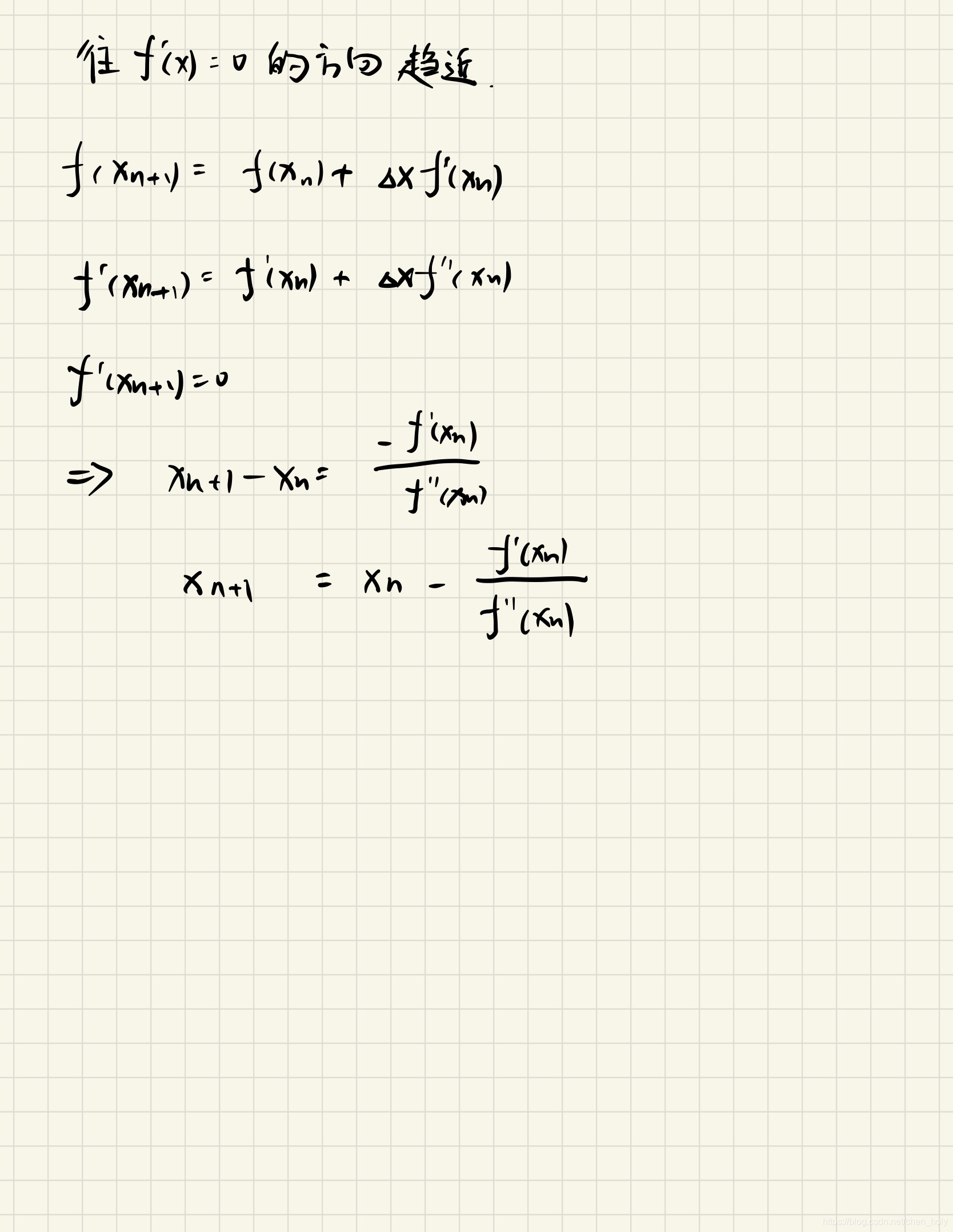特征工程
机器学习算法
K近邻算法
- 原理
每个样本都能用最接近它的k个邻居代表
- 流程
计算目标与所有样本之间的距离,选出距离最小的前K个样本,K个样本中占比最高的类别即为目标类别
- KNN三要素
K值的选取
距离度量方式
分类决策规则
- K值选取方式
交叉验证
- K值对模型结果的影响
较小的K值,减少训练误差,但容易过拟合
较大的K值,减少泛化误差,但训练误差会上升
- 分类决策规则
分类:
多数表决法,加权表决
回归:
平均法
- 优点 和 缺点
优点:
1. 思想简单,即可分类也可回归
2. 可用于非线性分类
3. 不需要对数据做假设,对异常点不敏感
4. 能处理类域交叉,重叠较多场景
缺点:
1. 计算量大,预测速度较慢,尤其样本,特征非常多的时候
2. 样本不平衡时分类结果不好,对稀有类别的预测准确率比较低
3. 相比决策模型,KNN可解释性不强
线性回归
逻辑回归
决策树
深度学习算法
其他
正则化
参考博客:
L1、L2正则化知识详解
比较全面的L1和L2正则化的解释
- 正则化是如何防止过拟合的
降低模型复杂度
- L1正则化,L2正则化
正则化通过降低模型复杂度,减少过拟合风险
L1正则化通过稀疏参数(减少参数的数量)来降低模型复杂度,具有特征选择功能
L2正则化通过减小参数的大小来降低模型复杂度
- 为什么L1正则化具有稀疏性,L2正则化却使参数变小
推导 带L1正则 或 L2正则的参数更新公式:
我们发现带L1正则的参数更新倾向减去一个常数,较L2更新更容易趋向0
带L2正则的参数更新倾向于比例放缩,使整体参数变小
BN
参考博客:
不请自来,BN本质上解决的是反向传播过程中的梯度问题。
- BN流程
对同一批次输入的数据进行标准归一化
缩放,偏移
- BN作用
保证同一层输入数据同分布,同时解决了反向传播中梯度爆炸梯度消失问题
每一层输入数据同分布是使用训练集训练模型有效的前提
如果不使用BN,不断的非线性变化使得同一层输入的分布发生了变化(层间Covariate Shift)
使用BN后强制使每一层的输入分布回到均值0方差1的分布中,类似数据预处理步骤中的标准归一化
同时BN的过程中增加两个调节参数(scale和shift), 避免了由w的scale导致的梯度消失与梯度爆炸问题
- 为什么会出现梯度消失和梯度爆炸
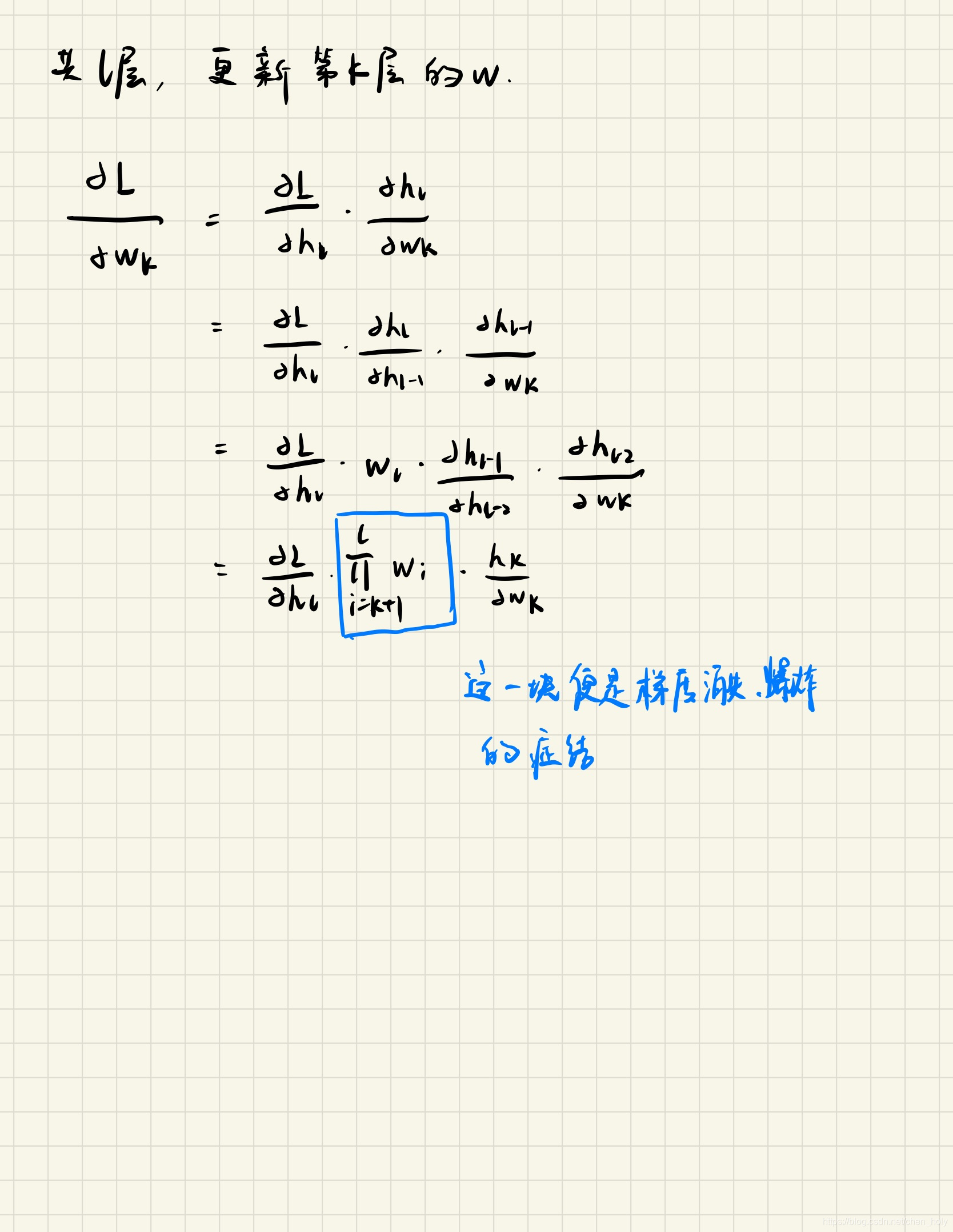
梯度反向传播的核心是链式求导法则
反向传播时,经过该层的梯度要乘以该层的参数
梯度下降
参考博客:
常见的几种最优化方法(梯度下降法、牛顿法、拟牛顿法、共轭梯度法等)
梯度下降法的推导(非常详细、易懂的推导)
关于梯度下降法和牛顿法的数学推导
梯度下降法和牛顿法的总结与比较
牛顿法与Hessian矩阵
- 梯度下降缺点, 批量梯度下降BGD,随机梯度下降SGD,MBGD:
梯度下降缺点:
靠近极小值时收敛速度减慢
BGD优点:
每次迭代参数朝着整体最优的方向更新
BGD缺点:
每次迭代需要计算全部数据,更新速度较慢
SGD优点:
更新参数速度快
SGD缺点:
受噪音影响大,每次迭代不一定朝着整体最优方向更新,容易出现“之”字型下降
- 为什么参数往这个方向更新loss能减少,为什么负梯度方向loss下降最快
一阶泰勒展开的推导过程
- 牛顿法应用
1. 求方程的根;
2. 求解最优化方法;
- 牛顿法参数更新推导
往 f′(x) = 0 的方向推导
优化器
参考博客:
深度学习——优化器算法Optimizer详解(BGD、SGD、MBGD、Momentum、NAG、Adagrad、Adadelta、RMSprop、Adam)
什么是指数加权平均、偏差修正?