from sklearn.datasets import load_iris
import pandas as pd
import numpy as np
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier,export_graphviz
from sklearn.metrics import auc, roc_curve, classification_report
import os
#信息熵:代表这系统的不确定度 ,信息熵大,系统越混乱,不确定性就越大;信息熵越小,系统越稳定,不确定性就越小
#
# # 定义两个概率分布列表
# lst = [0.25, 0.25, 0.25, 0.25]
# lst1 = [0.7, 0.2, 0.05, 0.05]
#
# # 计算并打印两个列表的熵
# print(entropy(lst)) # 对于均匀分布,熵最大,为 2
# print(entropy(lst1)) # 对于非均匀分布,熵小于 2
#条件熵H(Y|X)
#H(Y∣X)=∑x∈X p(x)H(Y∣X=x)
# 其中 p(x) 是 X 取值为 x 的概率,H(Y∣X=x) 是在 X 取值为 x 的条件下 Y 的熵
#给定随机变量X的条件下,Y的熵
"""
专业(X)性别(M)
数学 M
IT M
英语 F
数学 F
数学 M
IT M
英语 F
数学 F
"""
# def entropy(p):
# # 使用列表推导式和生成器表达式来计算非零元素的 -t * log2(t)
# return -np.sum(t * np.log2(t) for t in p if t != 0)
# #x的概率分布
# x=[0.5,0.25,0.25]
# #y的盖里分布
# y=[0.5,0.5]
# # 给定x的条件,Y的概率, 为计算 H(Y∣X=x)做准备
# x_0_y=[0.5,0.5]
# x_1_y=[1]
# x_2_y=[1]
# # 集合
# x_y=[[0.5,0.5],[1],[1]]
# H_X=entropy(x) #1.5
# # print(H_X)
# #y的信息熵
# # H_Y=entropy(y)
# # print(H_Y) # 1.0
#
# def conditional_entropy(arr,p_x):
# total=0.0
# for index,i in enumerate(arr):
# #计算 给定x的条件下的y的熵
# total += entropy(i) * p_x[index]
# return total
# H_X_Y=conditional_entropy(x_y,x)
# print(H_X_Y)
#
# #x和y发生的概率p(x,y)
# p_x_y=[0.25,0.25,0.25,0.25]
#事件(x,y)发生的熵 - X发生的熵=给定X条件下y产生的熵,conditional_entropy()等价
# H_X_and_Y=entropy(p_x_y)
# H_X_Y= H_X_and_Y - H_X
# 互信息 I(X;Y),联合熵H(X,Y),条件熵
# H(X,Y)=H(X) +H(Y)-I(X:Y)=H(X/Y)+I(X;Y)+H(Y/X)
"""
决策树是一种非常常用的有监督的分类算法
决策树分为两大类:分类树和回归树,前者用于分类标签值,后者用于预测连续值,
常用算法有ID3、C4.5、CART等
决策树是通过“纯度”来选择分割特征属性点的
决策树纯度量化
决策树的构建是基于样本概率和纯度进行构建操作的,那么进行判断数据集
是否“纯”可以通过三个公式进行判断,分别是Gini系数、熵(Entropy)、
错误率,这三个公式值越大,表示数据越“不纯”;越小表示越“纯”;实
践证明这三种公式效果差不多,一般情况使用熵公式
"""
#决策树构建过程
#信息熵
def entropy_pure(p):
return -np.sum(t * np.log2(t) for t in p if t !=0)
#错误率
def err(p):
return 1-np.sum(t **2 for t in p)
#Gini系数
def gini(p):
return 1-max(p)
def h(p):
"""
决策树的纯度量化
:param p:
:return:
"""
return entropy_pure(p)
# return gini(p)
# return err(p)
# 一、第一个判断节点的选择
# 1.0 计算整个数据集的纯度(样本数10个,3个是,7个否)
"""
拥有房产(是否) 婚姻状态(单身、离婚、已婚) 收入 不能偿还债务(否是)
是, 单身, 125, 否
是, 离婚, 220, 否
是, 已婚, 110, 否
是, 离婚, 60, 否
否, 已婚, 100, 否
否, 单身, 100, 否
否, 离婚, 95, 是
否, 单身, 85, 是
否, 已婚, 75, 否
否, 单身, 90, 是
"""
#这个决策树是单变量决策树
# H(D) 就是标签的信息熵
p=[0.7,0.3]
H_D=h(p)
print(H_D)
# 1.1 计算以拥有房产作为分割点的时候条件熵(遍历数据计算x1为是和否的概率)
# 第一个分支: 是;样本数目:4,全部为否
# ‘是’ 发生 概率是0.4
p1=0.4
# ‘是’ 条件下的标签结果为否 的概率是1,为是的概率是0
H_1=h([1,0])
print(H_1)
# 第二个分支:否;样本数目:6,3个是,3个否
# ‘否’ 发生 概率是0.4
p2=0.6
# ‘否’ 条件下的标签结果为否 的概率是0.5,为是的概率是0.5
H_2=h([0.5,0.5])
# H(D|A) A 这个指的是 是和否 的条件 ,注意区分标签是和否
# D和A一起发生的概率有:
p_A_D=[0.4,0.3,0.3]
H_A=h([0.4,0.6])
H_D_A=h(p_A_D)-H_A
# H_D_A还有另外一种算法 : H_D_A=0.4* H_1 +0.6* H_2 - H_A
# sys.exit()
# gain 信息增益度
gain_1=H_D-H_D_A
print("以拥有房产作为划分特征的时候,信息增为:{}".format(gain_1))
# # todo:信息增益率
gain_rate_1=gain_1/H_A
print("以拥有房产作为划分特征的时候,信息增率为:{}".format(gain_rate_1))
#同理分别计算 婚姻状态 收入 作为决策树的分裂属性
# 婚姻状态
# 单身 :样本数目 :4个, 否为2个,是为2个
p3=0.4
H_1=h([0.5,0.5])
#已婚 :样本数量 :3个 全部为否
p4=0.3
H_2=h([1,0])
#离婚 样本数量3个 2个否,1个是
p5=0.3
H_3=h([2/3,1/3])
p_A_D=[0.2,0.2,0.3,0.2,0.1]
H_A=h([0.4,0.3,0.3])
H_D_A=h(p_A_D)-H_A
#信息增益度
gain_2=H_D-H_D_A
#信息增益率
gain_rate_2=gain_1/H_A
print("以婚姻状态作为划分特征的时候,信息增为:{}".format(gain_2))
print("以婚姻状态作为划分特征的时候,信息增为:{}".format(gain_rate_2))
# 收入
#收入是个连续的值,需要找出split_point,大于 97.5
# 大于97.5 样本数量:5 ,全部为否
p6=0.5
H_1=h([1,0])
#小于 97.5 :样本数量为5个, 2个否,3个是
p7=0.5
H_2=h([0.4,0.6])
p_A_D=[0.5,0.2,0.3]
H_A=h([p6,p7])
H_D_A=h(p_A_D)-H_A
#信息增益度
gain_3=H_D-H_D_A
#信息增益率
gain_rate_3=gain_1/H_A
print("以收入作为划分特征的时候,信息增为:{}".format(gain_3))
print("以收入作为划分特征的时候,信息增为:{}".format(gain_rate_3))
# 信息增益度越大,该特征属性就应该在决策树的上层,此处的决策树从上到下依次是,收入,拥有房产,婚姻状态,
# 因此根据上述 信息增益率 决策树的第一个节点是收入 97.5 ,小于97.5
# 二、针对于左子树继续划分(年收入小于等于97.5的数据;样本数目:5,3个是,2个否)
"""
拥有房产(是否) 婚姻状态(单身、离婚、已婚) 收入 不能偿还债务(否是)
是, 离婚, 60, 否
否, 离婚, 95, 是
否, 单身, 85, 是
否, 已婚, 75, 否
否, 单身, 90, 是
"""
# H(D) 样本数目:5,3个是,2个否
p_D_1=[0.4,0.6]
H_D_1=h(p_D_1)
# 2.1 计算以房产作为分割点的时候条件熵
# 第一个分支: 是;样本数目:1,全部为否
p11=0.2
H_11=h([1,0])
# 第二个分支:否;样本数目:4,3个是,1个否
p22=0.8
H_22=h([0.25,0.75])
#H(D|A)
H_A_D=p11*H_11+p22*H_22
gain_11=H_D_1-H_A_D
print("决策树第二个节点选择:以房产作为划分特征的时候,信息增益为:{}".format(gain_11))
# 2.2 计算以婚姻情况作为分割点的时候条件熵(遍历数据计算x2为单身、离婚、已婚的概率)
# 婚姻状态
# 离婚 样本数量:2个, 1个为否,1个为是
p33=0.4
H_33=h([0.5,0.5])
# 单身 样本数量: :2个 ,均为是
p44=0.4
H_44=h([0,1])
#已婚 样本数量:1个, 1个否
p55=0.2
H_55=h([1,0])
#H(D|A)
H_A_D=0.4*H_33 + 0.4 * H_44 +0.2*H_55
gain_22=H_D_1-H_A_D
print("决策树第二个节点选择:以婚姻作为划分特征的时候,信息增益为:{}".format(gain_22))
# 因为gain_22>gain_11,因此决策树的第二个节点:婚姻状态
# 三、针对于右子树继续划分(年收入大于97.5的数据;样本数目:5,5个否 --> 不需要划分)
# 四、针对于第一个分支的子树继续划分(单身的数据;样本数目:2,2个是 --> 不需要划分)
# 五、针对于第二个分支的子树继续划分(离婚的数据;样本数目:2,1个是 1个否)
"""
拥有房产(是否) 婚姻状态(单身、离婚、已婚) 收入 不能偿还债务(否是)
是, 离婚, 60, 否
否, 离婚, 95, 是
"""
# 针对离婚
# 计算以婚姻情况作为分割点的时候条件熵 样本数量 2个,1个否 1个是
H_D_2=h([0.5,0.5])
#以房产作为分割点
# 第一个分支:是, 样本数量:1个 ,1个否
p_111=0.5
H_111=h([1,0])
# 第一个分支:否, 样本数量:1个 ,1个是
p_222=0.5
H_222=h([0,1])
H_A_D=0.5*H_111+p_222*H_222
gain_333=H_D_2-H_A_D
print(gain_333)
# TODO: 自己补全
# 六、针对于第三个分支的子树继续划分(已婚的数据;样本数目:1,1个否 --> 不需要划分)
#这个里的数据是经过处理的
# irs_data=load_iris()
# print(irs_data)
#读取数据
# header必须要加上,否则会以第一条数据
irs_data=pd.read_csv('../datas/iris.data',header=None,names=['A','B','C','D','cla'])
# print(irs_data)
#获取培训集,目标集,panda.iloc(行索引,列索引),是闭开
X=irs_data.iloc[:,:4]
X=np.asarray(X,dtype=np.float64)
# print(X.dtype)
Y=irs_data.iloc[:,4]
# print(Y)
#将目标转为数字
labelEncoder=LabelEncoder()
Y=labelEncoder.fit_transform(Y)
# print(Y)
# 训练集,测试集数据划分
x_train,x_test,y_train,y_test=train_test_split(X,Y,train_size=0.7,random_state=3)
# 模型创建
# 六、模型对象的构建
"""
def __init__(self,
criterion="gini",
splitter="best",
max_depth=None,
min_samples_split=2,
min_samples_leaf=1,
min_weight_fraction_leaf=0.,
max_features=None,
random_state=None,
max_leaf_nodes=None,
min_impurity_decrease=0.,
min_impurity_split=None,
class_weight=None,
presort=False)
criterion: 给定决策树构建过程中的纯度的衡量指标,可选值: gini、entropy, 默认gini
splitter:给定选择特征属性的方式,best指最优选择,random指随机选择(局部最优)
max_features:当splitter参数设置为random的有效,是给定随机选择的局部区域有多大。
max_depth:剪枝参数,用于限制最终的决策树的深度,默认为None,表示不限制
min_samples_split=2:剪枝参数,给定当数据集中的样本数目大于等于该值的时候,允许对当前数据集进行分裂;如果低于该值,那么不允许继续分裂。
min_samples_leaf=1, 剪枝参数,要求叶子节点中的样本数目至少为该值。
class_weight:给定目标属性中各个类别的权重系数。
"""
"""
需要注意的是,如果max_depth设置得过高,
决策树可能会过于复杂,导致过拟合;而如果设置得过低
,决策树可能会过于简单,导致欠拟合。因此,在选择max_depth值时,
需要综合考虑模型的性能、训练数据的规模以及特征的数量等因素。
总的来说,max_depth是决策树模型中一个重要的超参数,
通过合理设置该参数,可以在提高模型性能的同时避免过拟合和欠拟合的风险。
"""
algo = DecisionTreeClassifier(max_depth=3)
#模型训练
algo.fit(x_train,y_train)
#模型预测
y_predict=algo.predict(x_test)
#模型评估
s=algo.score(x_test,y_test)
print(s)
# 八、模型效果的评估
# print("各个特征属性的重要性权重系数(值越大,对应的特征属性就越重要):{}".format(algo.feature_importances_))
# print("训练数据上的分类报告:")
# print(classification_report(y_train, algo.predict(x_train)))
# print("测试数据上的分类报告:")
# print(classification_report(y_test, y_predict))
# print("训练数据上的准确率:{}".format(algo.score(x_train, y_train)))
# print("测试数据上的准确率:{}".format(algo.score(x_test, y_test)))
test1 = [x_test[6]]
print(test1)
print("预测函数:")
print(algo.predict(test1))
print("预测概率函数:")
print(algo.predict_proba(test1))
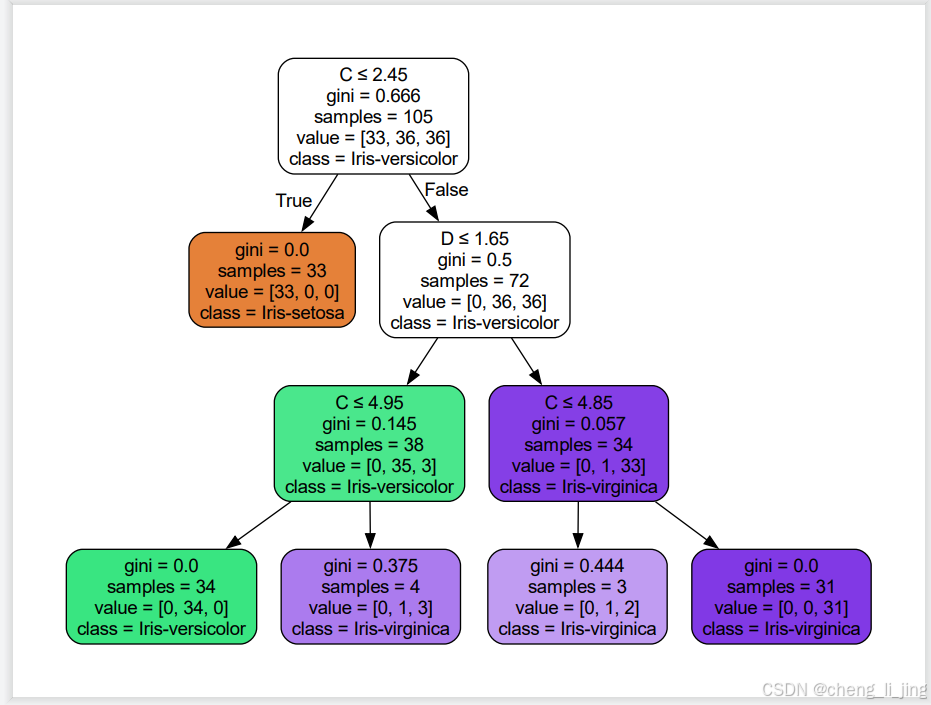
# 导出决策树为 DOT 格式
dot_data = export_graphviz(algo, out_file=None,
feature_names=['A', 'B', 'C', 'D'], # 特征名称
class_names=labelEncoder.classes_, # 目标类别名称
filled=True, rounded=True, # 图形样式
special_characters=True) # 允许特殊字符(如希腊字母)
# 将 DOT 数据写入文件
graph_file = "iris_decision_tree.dot" # 文件名(包含路径)
with open(graph_file, 'w') as f:
f.write(dot_data)
# 使用 Graphviz 将 DOT 文件转换为 PNG 图像
# 注意:这个命令需要在命令行或终端中手动执行,或者您可以使用 Python 的 subprocess 模块来执行它
# 方式一:(命令行)
# 在命令行或终端中执行以下命令:(转为pdf 或者 png)
# dot -Tpng iris_decision_tree.dot -o iris_decision_tree.png
# 或者
# dot -Tpdf iris_decision_tree.dot -o iris_decision_tree.pdf
# 如果您想在 Python 脚本中自动执行这个命令,可以使用以下代码:
try:
os.system(f"dot -Tpng {graph_file} -o {graph_file.replace('.dot', '.png')}")
except Exception as e:
print(f"无法生成 PNG 图像。请确保已安装 Graphviz,并在系统路径中可用。错误:{e}")
import pydotplus
#方式三:
graph = pydotplus.graph_from_dot_data(dot_data)
graph.write_png("iris_tree.png")
graph.write_pdf("iris_tree.pdf")
conda 安装 pydotplus