[电路]系列文章目录
1-发出功率和吸收功率关系
2-独立源和受控源
3-基尔霍夫定律
4-两端电路等效变换、电阻串并联
5-电压源、电流源的串联和并联
6-电阻的星形连接和角形连接等效变换(星角变换)
7-实际电源模型和等效变换
8-无源一端口网络输入电阻
9-电路的图及相关概念
10-支路电流法
11-网孔电流法
12-回路电流法
13-结点电压法
14-叠加定理和齐性定理
15-替代定理
16-戴维宁定理和诺顿定理
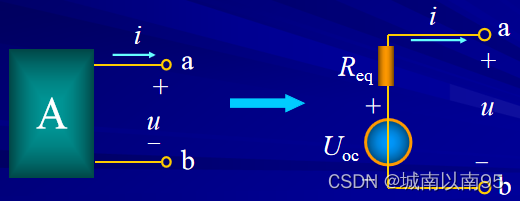
一、戴维宁定理
1 定义
任何一个线性含源一端口网络,对外电路来说,总可以用一个电压源和电阻的串联组合来等效置换;此电压源的电压等于外电路断开时端口处的开路电压 u o c u_{oc} uoc,而电阻等于一端口的输入电阻(或等效电阻 R e q R_{eq} Req)。
2 图示说明
3 说明
- 外电路可以是任意的线性或非线性电路,外电路发生改变时,含源一端口网络的等效电路不变(伏-安特性等效)。
- 当一端口内部含有受控源时,控制电路与受控源必须包含在被化简的同一部分电路中。
4 例题
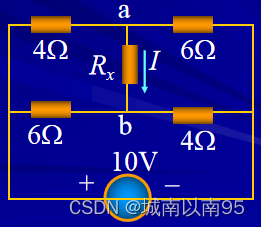
题目:
计算
R
x
R_x
Rx 分别为
1.2
Ω
1.2\Omega
1.2Ω 和
5.2
Ω
5.2\Omega
5.2Ω 时的电流
I
I
I。
分析:
由于电路中
R
x
R_x
Rx 阻值会发生变化,而其他部分不变,可以将
R
x
R_x
Rx 支路断开,将剩余部分看成一个含源一端口网络。
解答:
(1)将
R
x
R_x
Rx 支路断开,将剩余部分看成一个含源一端口网络。
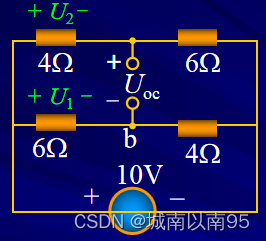
(2)求解含源一端口网络的开路电压。
U
o
c
=
U
1
−
U
2
=
−
10
×
4
4
+
6
+
10
×
6
4
+
6
=
6
−
4
=
2
V
U_{oc} = U_1 - U_2 = -10\times \frac {4}{4+6}+10 \times \frac {6}{4+6} = 6-4=2V
Uoc=U1−U2=−10×4+64+10×4+66=6−4=2V(3)计算等效电阻
R
e
q
R_{eq}
Req。
R
e
q
=
4
×
6
4
+
6
+
4
×
6
4
+
6
=
4.8
Ω
R_{eq}= \frac {4\times 6}{4+6}+\frac {4\times 6}{4+6}=4.8\Omega
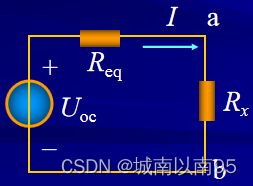
Req=4+64×6+4+64×6=4.8Ω(4)将上述含源一端口网络化为戴维宁等效电路。
(5)当
R
e
q
=
1.2
Ω
R_{eq}=1.2\Omega
Req=1.2Ω 时,计算电流
I
I
I。
I
=
U
o
c
R
e
q
+
+
R
x
=
0.333
A
I=\frac {U_{oc}}{R_{eq}++R_{x}}=0.333A
I=Req++RxUoc=0.333A(6)当
R
e
q
=
5.2
Ω
R_{eq}=5.2\Omega
Req=5.2Ω 时,计算电流
I
I
I。
I
=
U
o
c
R
e
q
+
+
R
x
=
0.2
A
I=\frac {U_{oc}}{R_{eq}++R_{x}}=0.2A
I=Req++RxUoc=0.2A
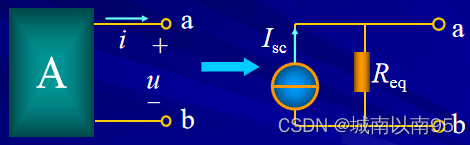
二、诺顿定理
1 定义
任何一个含源线性一端口电路,对外电路来说,可以用一个电流源和电阻的并联组合来等效置换;电流源的电流等于该一端口的短路电流,电阻等于该一端口的输入电阻。
2 图示说明
3 说明
一般情况,诺顿等效电路可由戴维宁等效电路经电源等效变换得到。
三、特殊说明
- 若一端口网络的等效电阻 R e q = 0 R_{eq}=0 Req=0,该一端口网络只有戴维宁等效电路,无诺顿等效电路。
- 若一端口网络的等效电阻
R
e
q
=
∞
R_{eq}=\infty
Req=∞,该一端口网络只有诺顿等效电路,无戴维宁等效电路。
更多内容关注微信公众号:城南以南95 回复 电路,即可获取资料,最近还会补充更新,关注不迷路
愿余生,不负岁月,不负自己。 喜欢就点个赞吧