信噪比、奈奎斯特采样定理、香浓定理定理与信噪比之间的关系的探讨
1 采样定理
1.1 奈奎斯特采样1
问:LTE中为什么使用30.72MHz的采样率去采样实际带宽为18MHz的信号?是否满足于“奈奎斯特采样定理”?
满足。
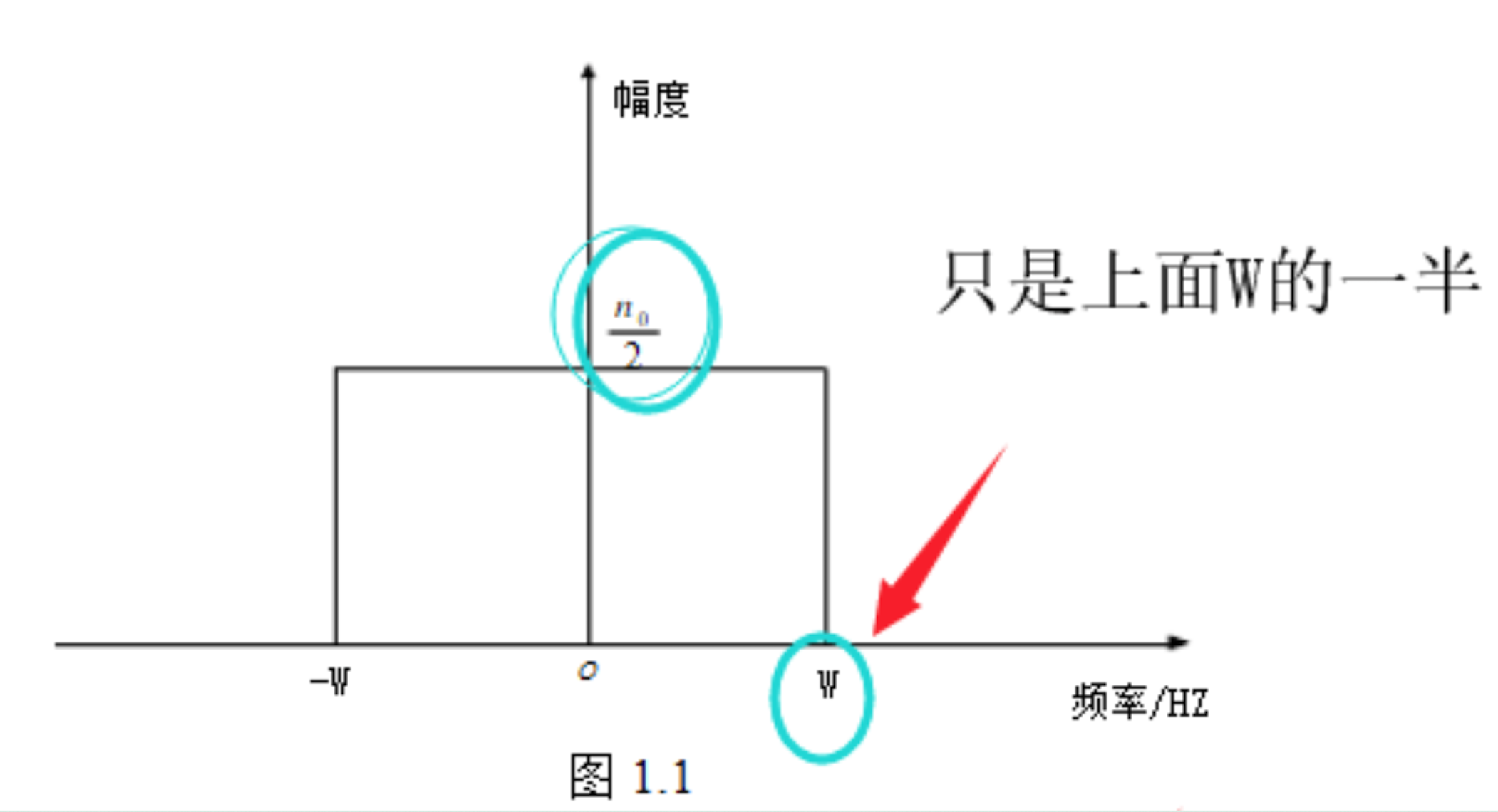
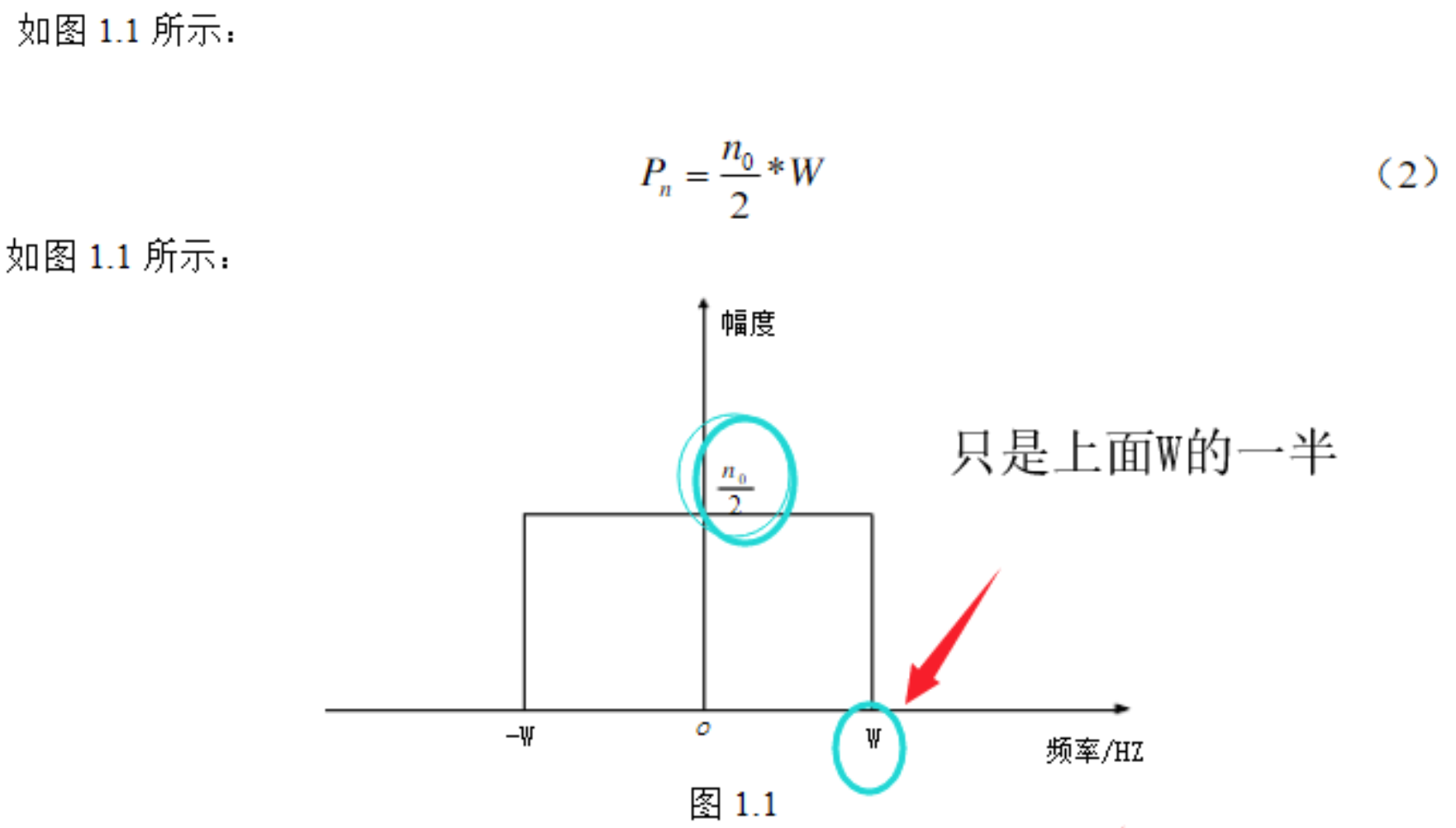
下图给出了白噪声信号的功率谱示意图,观察到带宽为W的白噪声在频谱图上占据了2W的宽度。
由于实信号具有共轭对称的频谱,从信息的角度来看,其负频谱部分是冗余的,将实信号的负频谱部分去掉,只保留正频谱部分的信号,其频谱不存在共轭对称性,所对应的时域信号应为复信号。复数信号处理的好处有:对于数字通信,在基带处理带通信号,可以使有效带宽减少一半,进而对于AD 的采样率要求,FFT的处理能力等都有改善。
解析信号的实部和虚部是正交的,是希尔伯特变换对,实部就是原信号或者说是实际存在的信号。由此我们可以利用希尔伯特变换得到解析信号。在雷达信号中,对于中频信号需要变换成零中频的复信号,称为视频信号(不一定解析,但是实部和虚部是正交的),有正交变换法,希尔伯特变换法,多相滤波法,插值法等多种方法,可以根据具体要求选取适当的方法。这些方法在雷达原理、软件无线电、通信理论等书籍和文献中都能找到很多。用复信号表示信号,构造解析信号减少一半频带是一个优点;用来表示实信号时,运算简便也是一个很重要的优点。2
另外,实际表示复数变量使用实部和虚部两个分量。复信号也一样,必须用实部和虚部两路信号来表示它,两路信号传输会带来麻烦,实际信号的传输总是用实信号,而在信号处理中则用复信号。3
信号处理引入复信号的原因只是一个——方便数学处理。实际信号不存在复信号,只存在实信号,将复信号按照数学规律叠加即可 得到实信号。
问:信号处理为什么引入复信号?4
对复数信号进行采样需要同时进行I、Q两路采样,但是这两路采样是相关的(相位相差pi/2),其中I路信号对应复信号的实部,即实际信号,Q信号对应复信号的虚部,引入Q信号即可进行复数计算处理。
复数信号与实数信号的关系如下:
c
o
s
k
w
t
=
(
e
x
p
(
j
k
w
t
)
+
e
x
p
(
−
j
k
w
t
)
)
/
2
;
cos kwt = (exp(jkwt)+exp(-jkwt))/2 ;
coskwt=(exp(jkwt)+exp(−jkwt))/2;
s
i
n
k
w
t
=
(
e
x
p
(
j
k
w
t
)
−
e
x
p
(
−
j
k
w
t
)
)
/
2
j
;
sin kwt = (exp(jkwt)-exp(-jkwt))/2j ;
sinkwt=(exp(jkwt)−exp(−jkwt))/2j;
a*cos kwt与b*sin kwt对应的exp(jkwt)与exp(-jkwt)的系数分别为(a/2+b/2j)、(a/2-b/2j),因此复信号的幅相系数是双边频谱(共轭对称)。复信号80M的带宽,对应的实际信号带宽只有40M。而且,要从复信号的频谱中提取实际信号的频谱(幅相),也需要进行一定的计算转换。对复信号进行采样需要满足 Fs>B,而对实信号进行采样需要满足Fs>2Fmax。(这个说法不太准确)
问:对I、Q信号两路进行采样,是不是采样一次相当于采样两次?
答:并非如此,I、Q信号是相参的,采样了I信号即能计算出相应的Q信号。但是这是建立在I路采样充分的基础上的(即Fs>2*Fmax),如果I路采样不充分,那么Q路的采样信号可以补充这种采样不充分。(那么,I、Q路同时采样只需要Fs>Fmax,就可以了吗?这一点需要进一步分析)
1.2 SNR与EbN0与香浓极限的推导
这一小节探讨香浓极限的计算过程。第一步给出香浓极限的结论。
信道容量为:
C
=
1
2
log
2
(
1
+
S
N
)
C=\frac{1}{2} \log _{2}\left(1+\frac{S}{N}\right)
C=21log2(1+NS)
由于信道的带宽为 B,所以如果要信号带宽也在 B 以内,则根据乃奎斯特采样定理,采样率必须满足:
F
s
≤
2
B
F_{s} \leq 2 B
Fs≤2B
所以单位时间内的信道容量为:
C
t
=
2
B
C
=
B
log
2
(
1
+
S
N
)
C_{t}=2 B C=B \log _{2}\left(1+\frac{S}{N}\right)
Ct=2BC=Blog2(1+NS)
对于AWGN信道,先推导出S/N与Eb/N0之间的关系:
S
N
=
E
b
T
b
N
0
2
⋅
2
B
=
E
b
N
0
⋅
R
b
B
\frac{S}{N}=\frac{\frac{E_{b}}{T_{b}}}{\frac{N_{0}}{2} \cdot 2 B}=\frac{E_{b}}{N_{0}} \cdot \frac{R_{b}}{B}
NS=2N0⋅2BTbEb=N0Eb⋅BRb
带入得到:
C
B
=
log
2
(
1
+
E
b
N
0
⋅
R
b
B
)
\frac{C}{B}=\log _{2}\left(1+\frac{E_{b}}{N_{0}} \cdot \frac{R_{b}}{B}\right)
BC=log2(1+N0Eb⋅BRb)
上图中的
R
b
R_b
Rb可以表示成为
R
b
=
f
s
∗
C
o
d
e
R
a
t
e
∗
M
o
d
e
R_b = fs*CodeRate*Mode
Rb=fs∗CodeRate∗Mode。假定
R
=
C
o
d
e
R
a
t
e
∗
M
o
d
e
R = CodeRate*Mode
R=CodeRate∗Mode,那么有如下结果:
S
N
=
2
R
E
b
N
0
\frac{S}{N}=2 R \frac{E_{b}}{N_{0}}
NS=2RN0Eb
因此我们知道AWGN波形信道容量为:
C
=
1
2
log
2
(
1
+
S
N
)
=
log
2
(
1
+
2
R
E
b
N
0
)
\begin{aligned} C &=\frac{1}{2} \log _{2}\left(1+\frac{S}{N}\right) \\ &=\log _{2}\left(1+\frac{2 R E_{b}}{N_{0}}\right) \end{aligned}
C=21log2(1+NS)=log2(1+N02REb)
如果C=R为常数,只需要求解上述方程,可得:
E
b
N
0
=
2
2
R
−
1
2
R
\frac{E_{b}}{N_{0}}=\frac{2^{2 R}-1}{2 R}
N0Eb=2R22R−1
这个结论与通信之美中的结论是一致的。这个结论满足于没有调制只有编码的条件下,但是明显有个问题就是不满足信噪比之间的转换关系(EsN0于EbN0之间的关系)。究竟是哪里出了问题?
IMPORTANT
有前辈曾对我说BPSK调制有3dB的增益,然而BPSK其实相当于只有编码没有调制。如果加上3dB的增益,那么符合这里的结果。
对于纯编码,R代表码率。这里传输的实际上是实数信号,(fs=2B)所以信噪比的关系如此。
E
b
N
0
=
2
2
R
−
1
2
R
\frac{E_{b}}{N_{0}}=\frac{2^{2 R}-1}{2 R}
N0Eb=2R22R−1
S
N
=
2
R
E
b
N
0
\frac{S}{N}=2 R \frac{E_{b}}{N_{0}}
NS=2RN0Eb
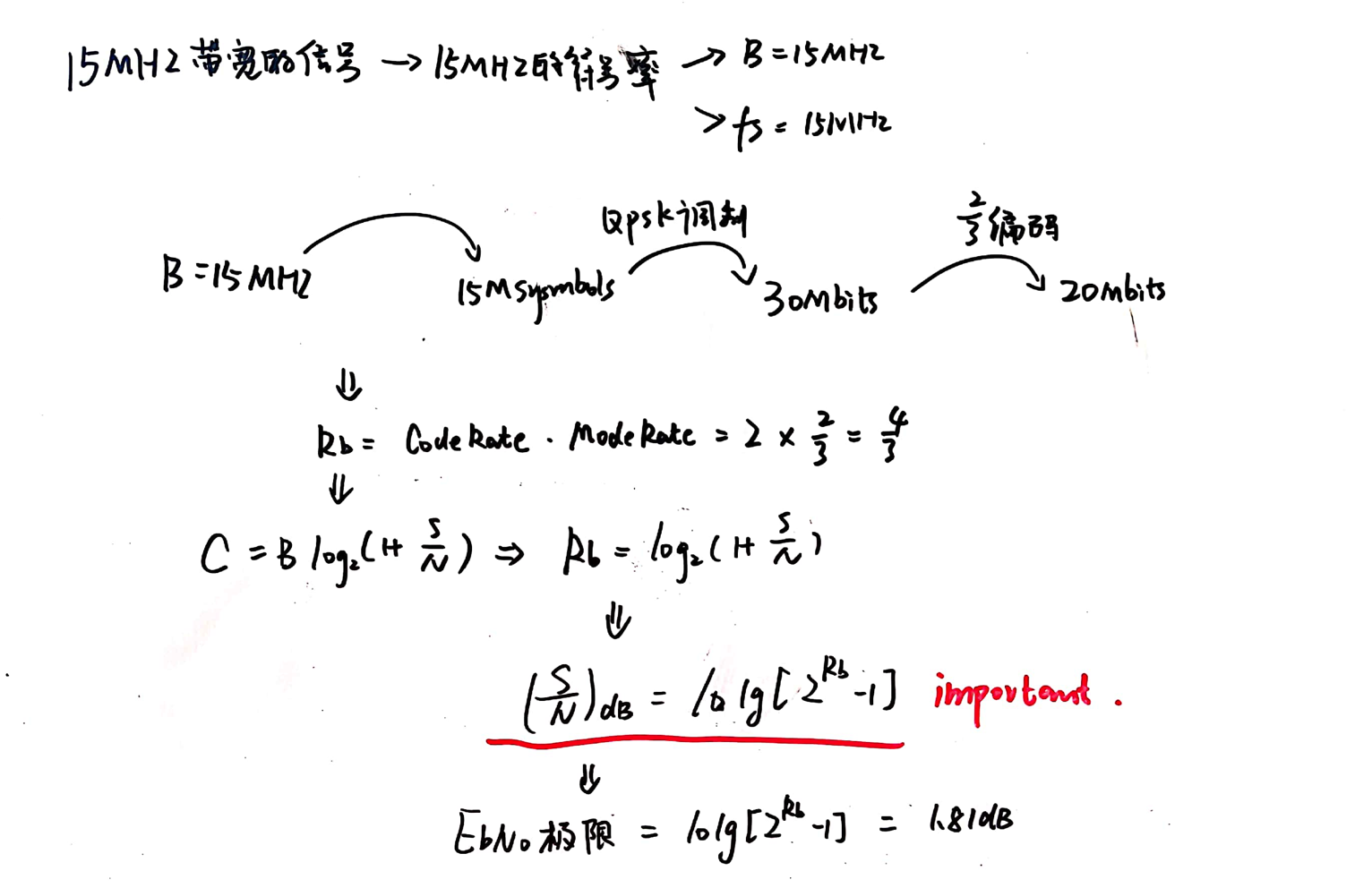
对于QPSK或者其他高阶的调制来说,有如下结论。这里传输的实际上是复数信号(fs = B),所以信噪比的关系是这样。而在通信链路中,均采用这样的方式去计算EbN0与EsN0之间的关系。
E
b
N
0
=
2
R
−
1
R
\frac{E_{b}}{N_{0}}=\frac{2^{R}-1}{R}
N0Eb=R2R−1
S
N
=
R
E
b
N
0
\frac{S}{N}=R \frac{E_{b}}{N_{0}}
NS=RN0Eb
其中$R = CodeRate*Mode $。
由此,我们便得到了香浓极限的计算方法。
2 证明过程5
3 仿真结果
3.1 初步结果论证
仿真基于下面的代码。
% EsN0 = -5.50 , EbN0 = -0.73 , error = 25889 , NumBit = 102400 ,pe = 2.528223e-01
% EsN0 = -5.00 , EbN0 = -0.23 , error = 22104 , NumBit = 102400 ,pe = 2.158594e-01
% EsN0 = -4.50 , EbN0 = 0.27 , error = 11904 , NumBit = 102400 ,pe = 1.162500e-01
% EsN0 = -4.00 , EbN0 = 0.77 , error = 719 , NumBit = 102400 ,pe = 7.021484e-03
% EsN0 = -3.50 , EbN0 = 1.27 , error = 0 , NumBit = 1024000 ,pe = 0
% EsN0 = -3.00 , EbN0 = 1.77 , error = 0 , NumBit = 1024000 ,pe = 0
% EsN0 = -2.50 , EbN0 = 2.27 , error = 0 , NumBit = 1024000 ,pe = 0
% EsN0 = -2.00 , EbN0 = 2.77 , error = 0 , NumBit = 1024000 ,pe = 0
仿真结果表明,在AWGN 信道下,码率为1/2 的Turbo 码在达到误比特率(BER) ≤ 10−5时,Eb/N0仅为约0.7dB (这种情况下达到信道容量的理想Eb/N0值为0db),远远超过了其他的编码方式,一时在信息和编码理论界引起了轰动。6
这里结果与我们的仿真结果是很接近的,有理由相信计算方式是正确的。
3.2 进一步结果论证
4 示例代码
下面代码提供turbo编解码模版,未添加符号匹配和调制等内容。
clear
close all
rng('default')
%% 系统参数
SlotBitLen = 1024;
EsN0_dBlist = [-3.5:0.5:0]-2;
% EsN0_dBlist = 100 ;
CodeRate = 1/3; % 码率
EbN0 = EsN0_dBlist - 10*log10( 1 * CodeRate) ; % 类似于BPSK调制必须有3dB的相差
Ns = 4;
sr = 8e6;
fs = Ns*sr;
M = 1;
%% 编码参数
nloop_up = 1e3;
nloop_down = 1e2;
error_up = 200;
[f1, f2] = getf1f2(SlotBitLen);
InterTbl = zeros(1,SlotBitLen);
for ii = 0:SlotBitLen-1
InterTbl(ii+1) = mod(f1*ii+f2*ii^2,SlotBitLen);
end
hTEnc = comm.TurboEncoder(poly2trellis(4, [13 15], 13), InterTbl + 1); % 简化方式
hTDec = comm.TurboDecoder(poly2trellis(4, [13 15], 13), InterTbl + 1, 10,'Algorithm','Max'); % 简化方式
%%
tic;
for EsN0_index = 1:length(EsN0_dBlist)
%% 统计
errcod = 0; errmod = 0;
lencod = 0; lenmod = 0;
expnumber = 0;
EsN0 = EsN0_dBlist(EsN0_index);
snr = EsN0 - 10*log10(Ns);
while( (errcod <error_up)&&(expnumber<nloop_up)||(expnumber<nloop_down) )
expnumber = expnumber + 1;
% 生成 bit
TCSrc = randi([0 1],1,SlotBitLen);
% 编码
TurboCodeOut = step(hTEnc, TCSrc.').';
ModeBitIn = TurboCodeOut;
Tx = 1-ModeBitIn*2;
Tx = Tx.*(1+1j)/sqrt(2);
% 加噪
% Rx = Tx + wgn(1,length(Tx),-EsN0);
Rx = awgn(Tx,EsN0,'measured');
TCDecSoftInfo = imag(Rx)+real(Rx);
% 解码
TCDDecOut = step(hTDec, -TCDecSoftInfo.').';
% 统计误码
errcod = errcod + biterr(TCSrc,TCDDecOut);
errmod = errmod + biterr(TCDecSoftInfo>0,TurboCodeOut);
lencod = lencod + SlotBitLen;
lenmod = lenmod + length(TurboCodeOut);
end
fprintf('%% EsN0 = %4.2f , EbN0 = %4.2f , error = %4.0f , NumBit = %4.0f ,pe = %d\n',...
EsN0 ,EbN0(EsN0_index), errcod ,lencod, errcod/lencod);
err_rate_cod(EsN0_index ) = errcod/lencod; % 统计解码误码率
err_rate_mod(EsN0_index ) = 1-errmod/lenmod; % 统计解调误码率
end
toc
信号采样、调制与搬移—对奈奎斯特定理的讨论 ↩︎
https://blog.csdn.net/u012923751/article/details/79643762?utm_source=blogxgwz5 ↩︎
《通信信号处理》张贤达 国防工业出版社 ↩︎
参考—通信之美 ↩︎
https://baike.baidu.com/item/Turbo%E7%A0%81/7518982?fr=aladdin ↩︎