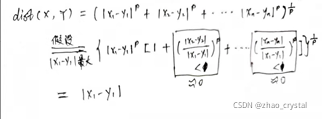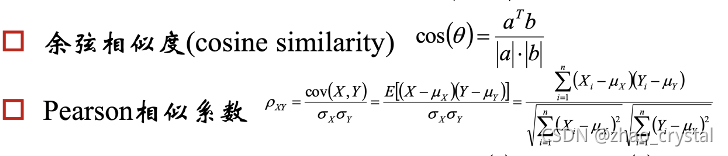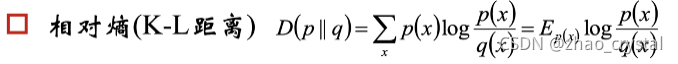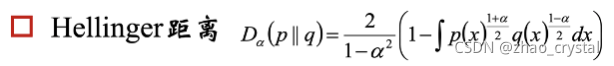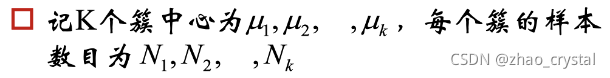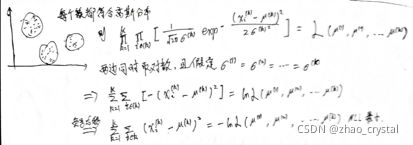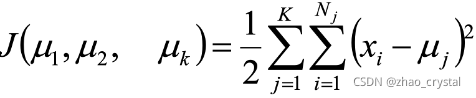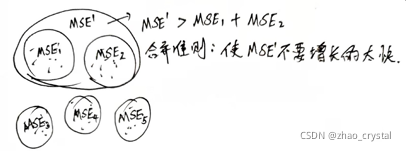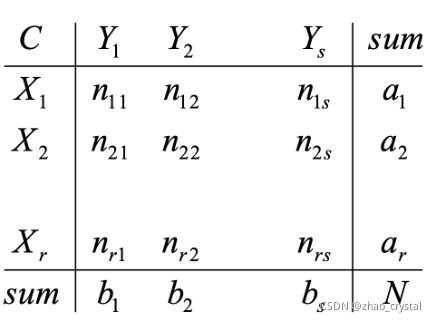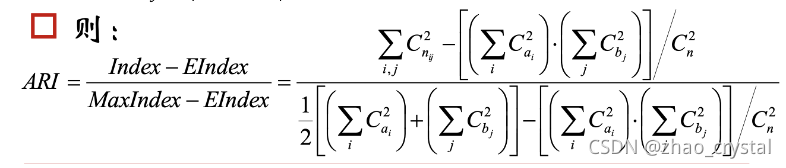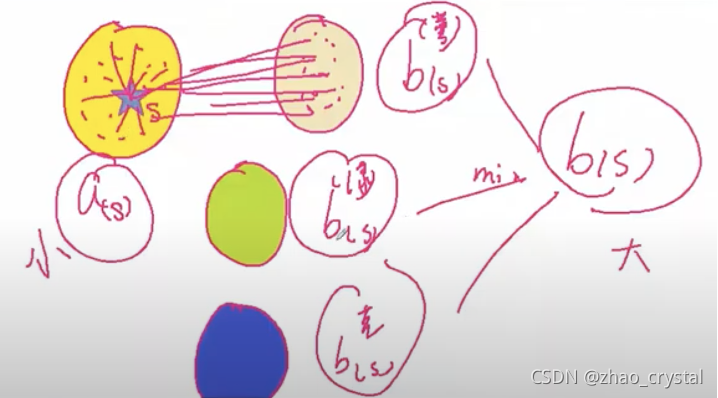目录
2.2 数据预处理:解决数据不均衡(两类差一个数量级以上)问题
5.5 AMI(Adjusted Mutual Information)调整互信息
1. 聚类的定义
聚类就是对大量未知标注的数据集,按数据的内在相似性将数据集划分为多个类别,使类别内的数据相似度较大而类别间的数据相似度较小。
2. 聚类的应用
2.1 降维
对于M篇文章,D1, D2, D3 …… Dm,假设已做好分词。
根据这M篇文章,得到一个词典word_dict = {W1, W2, W3, W4……Wv},假设共有v个词。
方式1: 0,1 矩阵(0代表没有出现过,1代表出现过)
若D1中出现过W1,则将相应位置置为1,否则置为0。其它同理。——>m纬v列的0,1矩阵。
方式2: 频数矩阵
若D1中出现过n次W1,则相应位置置为n,其它同理。——>m纬v列的频数矩阵。
方式3: tf-idf矩阵(某一特定文件内的高词语频率,以及该词语在整个文件集合中的低文件频率,可以产生出高权重的tf-idf。因此,tf-idf倾向于过滤掉常见的词语,保留重要的词语。)——>m纬v列的tf-idf矩阵。
一篇文章往往有成千上万字,且还是很多篇文章,v必定是很大的——>特征维度高。
解决办法:
通过将{W1, W2, W3, W4,……Wv}聚类,达到降纬的目的。假设降到200维。
矩阵分解Xm*v *C v*200 = Ym*200 (Kmeans VS 矩阵分解)
2.2 数据预处理:解决数据不均衡(两类差一个数量级以上)问题
假设正类有1000个样本,负类有400个样本。可将正类聚成10个堆,从每个堆中抽取50个样本,既保证了样本的多样性,又进行了降采样。
2.3 结果后处理
比如根据某些算法得到需要流量的用户,再根据某些维度特征进行聚类,得到哪些是高价值用户,哪些是低价值用户等。以便得到精准推荐。
3. 相似度/距离计算方法总结
3.1 Minkowski距离
p=1,曼哈顿距离
dist(X, Y) = |x1 – y1| + |x2 – y2| + |x3 – y3| +…… |xn-yn|
P=无穷大,切比雪夫距离
3.2 Jaccard
使用场景:
(1)对于集合场景:比如推荐的商品为集合A, 客户喜欢的商品为集合B。J = 1,说明推荐的和喜欢的相似度很高。推荐最有效。J=0,说明推荐的用户都不喜欢。
(2)对于物体检测,如下图所示,可根据Jaccard判断检测物体的准确度。A为检测出来物体的框,B为实际物体的轮廓。
3.3 cosine / Pearson 相似度/系数
当X,Y的均值为0时,Pearson相似系数退化为余弦相似度。
Pearson相似系数为0,线性不相关。
3.4 相对熵/K-L距离
K-L距离不对称。(比如你喜欢他的程度和他喜欢你的程度)
K-L距离为0 ——>独立。
3.5 Hellinger 距离
Hellinger对称, 非负距离。
4. 聚类算法
给定一个有N个对象的数据集,构造数据的K个簇,k<=n。满足下列条件:
- 每一个簇至少包含一个对象
- 每一个对象属于且仅属于一个簇
- 将满足上述条件的k个簇称作一个合理划分
基本思想:
对于给定的类别数目k,首先给出初始划分,通过迭代改变样本和簇的隶属关系,使得每一次改进之后的划分方案都较前一次好。
4.1 K-Means算法
k-Means算法,也被称为k-平均或k-均值,是一种广泛使用的聚类算法,或者称为其他聚类算法的基础。
k-means 要求每个簇的数据为正态分布,总体数据为混合高斯分布,即该模型为GMM(Gaussian mixture model)。切默认认为每个簇的方差相等。
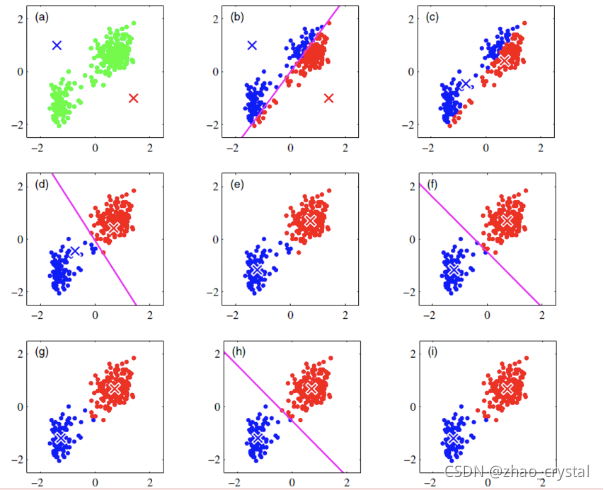
4.1.1 k-Means算法原理
k-Means过程如下图所示
4.1.2 k-Means的公式化解释
故,使用平方误差作为目标函数:
Ps:若使用其它相似度/距离度量?
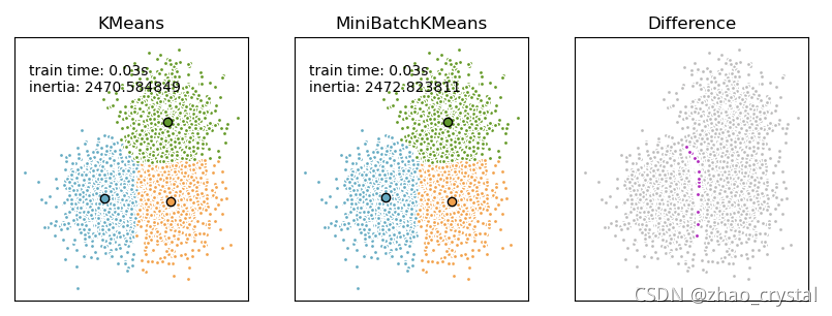
4.1.3 Mini-batch k-Means
Mini-batches are subsets of the input data, randomly sampled in each training iteration.
- In the first step, samples are drawn randomly from the dataset, to form a mini-batch. These are then assigned to the nearest centroid.
- In the second step, the centroids are updated.
mini-batch k-means produces results that are generally only slightly worse than the standard algorithm.
参考链接:https://scikit-learn.org/stable/modules/clustering.html#mini-batch-kmeans
4.1.4 k-Means中心初值的选择
k-Means是初值敏感的
(1) 随机选择
由于k-means对初值敏感,所以可能会出现sub-optimal clustering
(2) 经验预测
可根据先验知识预先给定,比如有一组身高数据,根据先验知识会分为两个簇,男,女。男生身高的中心值大概为1.75,女生身高的中心值大概为1.62。1.75和1.62即可作为k-means的中心初值。
(3) k-means++
参考链接https://en.wikipedia.org/wiki/K-means%2B%2B
4.1.5 k-Means k值的选择
(1) 使用经验(先验知识)
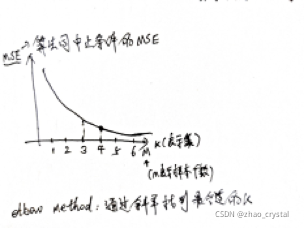
(2) Elbow Method
参考链接https://en.wikipedia.org/wiki/Elbow_method_(clustering)
4.1.6对k-Means的思考
(1)k-Medians
场景1: k-Means将簇中所有点的均值作为新质心,若簇中含有异常点,将导致均值偏离严重。
场景2: 对于离散特征,若可排序(比如: 优秀,好,良好,差),可用k-medians。若不可排序,则不能用。
以一维数据为例:
- 数组1,2,3,4,100的均值为22,显然距离“大多数”数据1,2,3,4比较远
- 改成求数组的中位数3,在该实例中更为稳妥
- 这种聚类方式即k-Medians聚类(k中值距离)
(2)二分k-Means
为克服K-Means算法收敛于局部最小值问题,提出了二分K-Means算法
二分K-Means算法首先将所有点作为一个簇,然后将该簇一分为二。之后选择其中一个簇继续进行划分,选择哪一个簇进行划分取决于对其划分是否可以最大程度降低SSE的值。上述基于SSE的划分过程不断重复,直到得到用户指定的簇数目为止。
步骤:
1. 将所有点看成一个簇;
2. 对每个簇,进行如下操作:
- 计算总误差
- 在给定的簇上进行K-Means聚类(k=2)
- 计算将该簇一分为二之后的总误差
3. 选择使得误差SSE/MSE最小的那个簇进行划分操作
重复2—3操作,直到达到用户指定的簇数目为止;
另一种做法:选择SSE/MSE最大的簇进行划分,直到簇数目达到用户指定的数目为止。
4.1.7 k-Means总结
4.2 Canopy 算法
虽然Canopy算法可以划归为聚类算法,但更多的可以使用Canpy算法做空间索引,其时空复杂度都很出色。
与传统的聚类算法(比如 K-means )不同,Canopy 聚类最大的特点是不需要事先指定 k 值( 即 clustering 的个数),因此具有很大的实际应用价值。与其他聚类算法相比,Canopy聚类虽然精度较低,但其在速度上有很大优势,因此可以使用 Canopy 聚类先对数据进行“粗”聚类,(摘自于Mahout一书:Canopy算法是一种快速地聚类技术,只需一次遍历数据就能得到结果,无法给出精确的簇结果,但能给出最优的簇数量。可为K均值算法优化超参数..K....)得到 k 值后再使用 K-means 进行进一步“细”聚类。
4.2.1 Canpy的算法原理
4.2.2 Canopy + K-means混合聚类
Canopy + K-means的混合聚类方式分为以下两步:
Step1:聚类最耗费计算的地方是计算对象相似性的时候,Canopy 聚类在第一阶段选择简单、计算代价较低的方法计算对象相似性,将相似的对象放在一个子集中,这个子集被叫做Canopy ,通过一系列计算得到若干Canopy,Canopy 之间可以是重叠的,但不会存在某个对象不属于任何Canopy的情况,可以把这一阶段看做数据预处理;
Step2:在各个Canopy 内使用传统的聚类方法(如K-means),不属于同一Canopy 的对象之间不进行相似性计算。
这个方法可以看出两点好处:首先,Canopy 不要太大且Canopy 之间重叠的不要太多的话会大大减少后续需要计算相似性的对象的个数;其次,类似于K-means这样的聚类方法是需要人为指出K的值的,通过Stage1得到的Canopy 个数完全可以作为这个K值,一定程度上减少了选择K的盲目性。
4.3 层次聚类方法
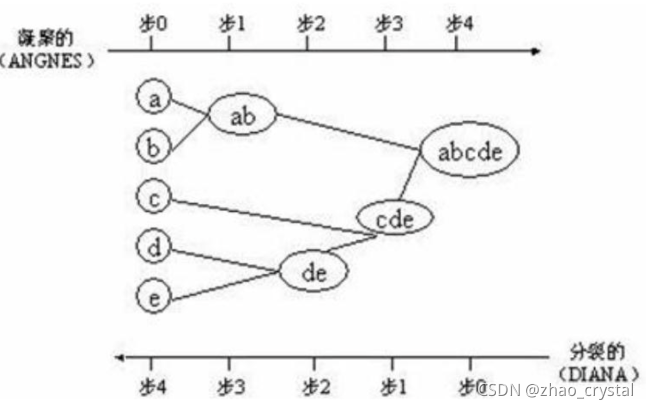
4.3.1 AGANS算法和DIANA算法
AGNES中簇间距离的不同定义
4.3.2 BIRCH算法
参考博客:BIRCH聚类算法原理 - 刘建平Pinard - 博客园
BIRCH的全称是利用层次方法的平衡迭代规约和聚类(Balanced Iterative Reducing and Clustering Using Hierarchies)
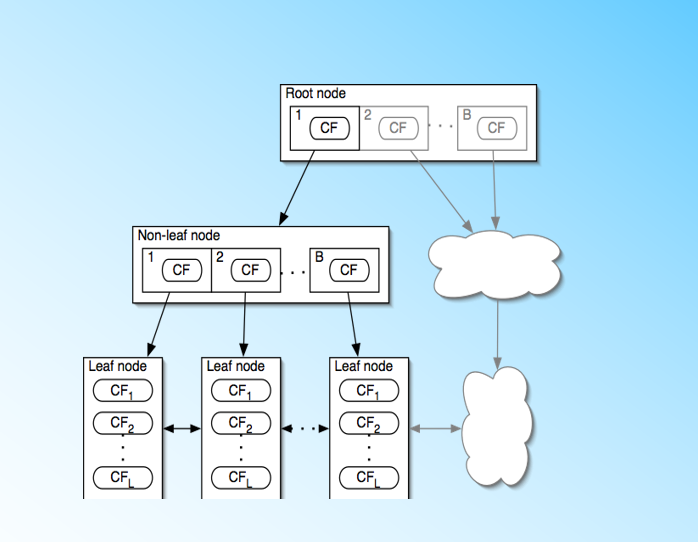
BIRCH算法利用了一个树结构来帮助我们快速的聚类,这个数结构类似于平衡B+树,一般将它称之为聚类特征树(Clustering Feature Tree,简称CF Tree)。这颗树的每一个节点是由若干个聚类特征(Clustering Feature,简称CF)组成。从下图我们可以看看聚类特征树是什么样子的:每个节点包括叶子节点都有若干个CF,而内部节点的CF有指向孩子节点的指针,所有的叶子节点用一个双向链表链接起来。
(1) 聚类特征CF与聚类特征树CF Tree
在聚类特征树中,一个聚类特征CF是这样定义的:每一个CF是一个三元组,可以用(N,LS,SS)表示。其中N代表了这个CF中拥有的样本点的数量,这个好理解;LS代表了这个CF中拥有的样本点各特征维度的和向量,SS代表了这个CF中拥有的样本点各特征维度的平方和。举个例子如下图,在CF Tree中的某一个节点的某一个CF中,有下面5个样本(3,4), (2,6), (4,5), (4,7), (3,8)。则它对应的N=5, LS=(3+2+4+4+3,4+6+5+7+8)=(16,30)(3+2+4+4+3,4+6+5+7+8)=(16,30), SS =(32+22+42+42+32+42+62+52+72+82)=(54+190)=244
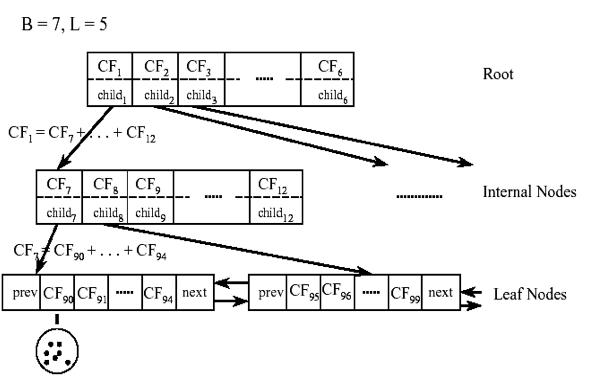
CF有一个很好的性质,就是满足线性关系,也就是𝐶𝐹1+𝐶𝐹2=(𝑁1+𝑁2,𝐿𝑆1+𝐿𝑆2,𝑆𝑆1+𝑆𝑆2)CF1+CF2=(N1+N2,LS1+LS2,SS1+SS2)。这个性质从定义也很好理解。如果把这个性质放在CF Tree上,也就是说,在CF Tree中,对于每个父节点中的CF节点,它的(N,LS,SS)三元组的值等于这个CF节点所指向的所有子节点的三元组之和。如下图所示:
从上图中可以看出,根节点的CF1的三元组的值,可以从它指向的6个子节点(CF7 - CF12)的值相加得到。这样我们在更新CF Tree的时候,可以很高效。
CF Tree的几个重要参数:
a. 每个内部节点的最大CF数 B
b. 每个叶子节点的最大CF数 L
c. 叶节点每个CF的最大样本半径阈值T。即在此CF中,所有样本点一定要在半径小于T的一个超体内。
对于上图中的CF Tree,限定了B=7, L=5, 也就是说内部节点最多有7个CF,而叶子节点最多有5个CF。
(2) 聚类特征树CF Tree的生成
定义好CF Tree的参数: 即内部节点的最大CF数B, 叶子节点的最大CF数L, 叶节点每个CF的最大样本半径阈值T。
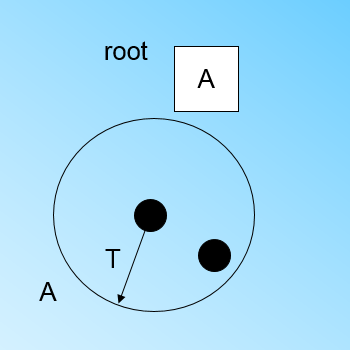
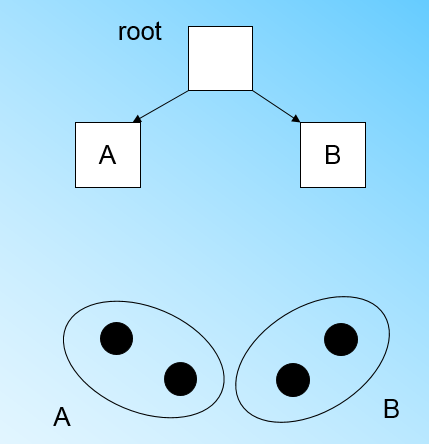
在最开始的时候,CF Tree是空的,没有任何样本,我们从训练集读入第一个样本点,将它放入一个新的CF三元组A,这个三元组的N=1,将这个新的CF放入根节点,此时的CF Tree如下图:
现在我们继续读入第二个样本点,我们发现这个样本点和第一个样本点A,在半径为T的超球体范围内,也就是说,他们属于一个CF,我们将第二个点也加入CF A,此时需要更新A的三元组的值。此时A的三元组中N=2。此时的CF Tree如下图:
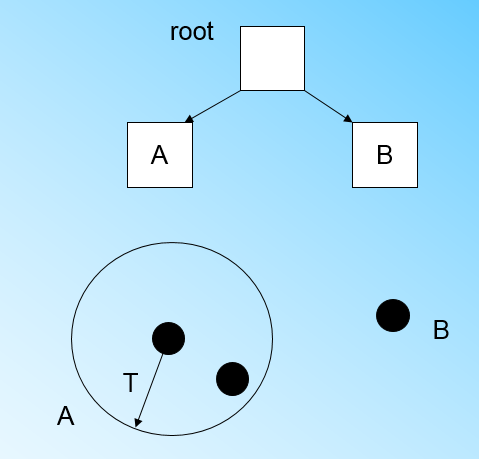
此时来了第三个节点,结果我们发现这个节点不能融入刚才前面的节点形成的超球体内,也就是说,我们需要一个新的CF三元组B,来容纳这个新的值。此时根节点有两个CF三元组A和B,此时的CF Tree如下图:
当来到第四个样本点的时候,我们发现和B在半径小于T的超球体,这样更新后的CF Tree如下图:
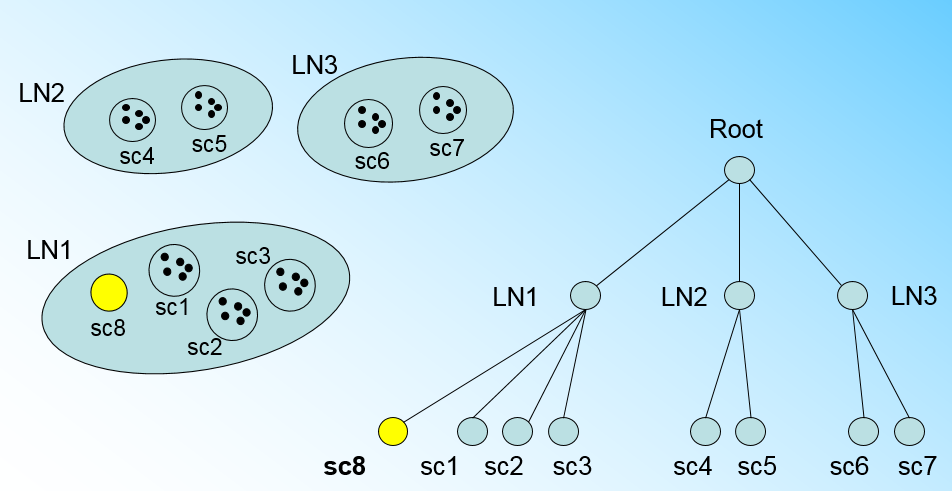
那个什么时候CF Tree的节点需要分裂呢?假设我们现在的CF Tree 如下图, 叶子节点LN1有三个CF, LN2和LN3各有两个CF。我们的叶子节点的最大CF数L=3。此时一个新的样本点来了,我们发现它离LN1节点最近,因此开始判断它是否在sc1,sc2,sc3这3个CF对应的超球体之内,但是很不幸,它不在,因此它需要建立一个新的CF,即sc8来容纳它。问题是我们的L=3,也就是说LN1的CF个数已经达到最大值了,不能再创建新的CF了,怎么办?此时就要将LN1叶子节点一分为二了。
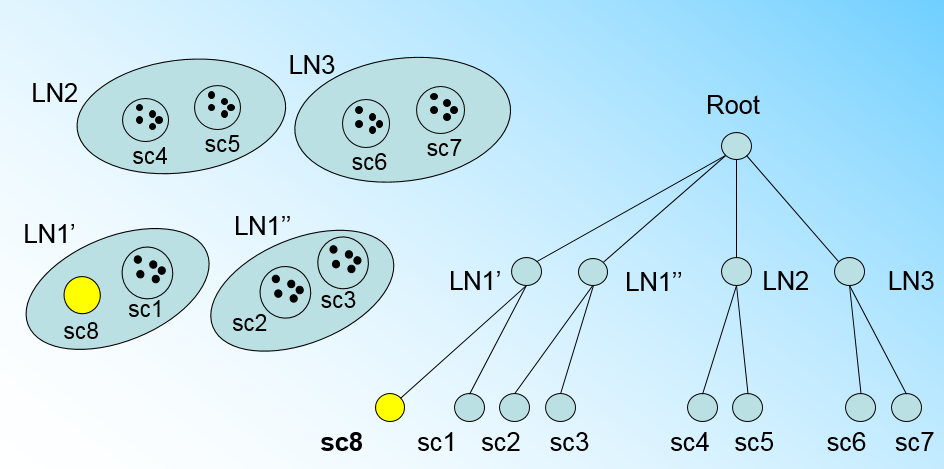
我们将LN1里所有CF元组中,找到两个最远的CF做这两个新叶子节点的种子CF,然后将LN1节点里所有CF sc1, sc2, sc3,以及新样本点的新元组sc8划分到两个新的叶子节点上。将LN1节点划分后的CF Tree如下图:
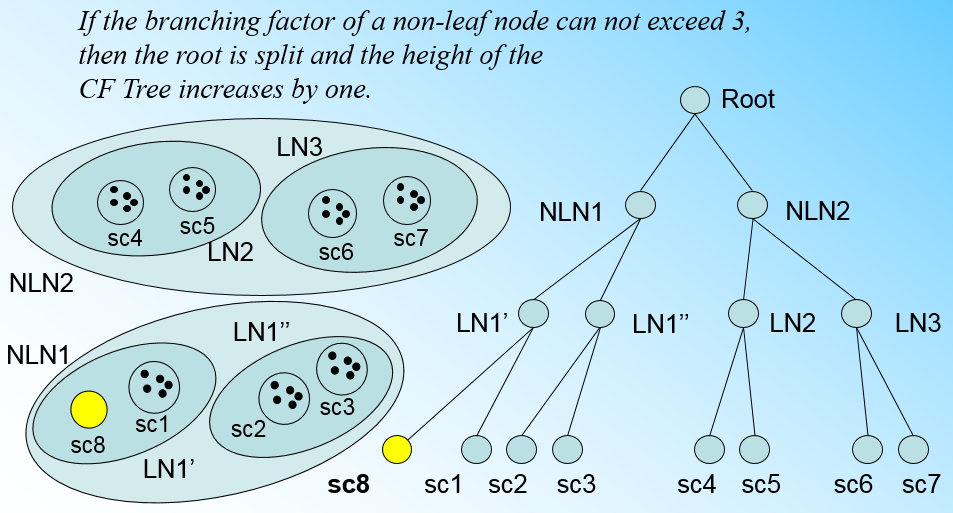
如果我们的内部节点的最大CF数B=3,则此时叶子节点一分为二会导致根节点的最大CF数超了,也就是说,我们的根节点现在也要分裂,分裂的方法和叶子节点分裂一样,分裂后的CF Tree如下图:
总结CF Tree的插入:
1. 从根节点向下寻找和新样本距离最近的叶子节点和叶子节点里最近的CF节点
2. 如果新样本加入后,这个CF节点对应的超球体半径仍然满足小于阈值T,则更新路径上所有的CF三元组,插入结束。否则转入3.
3. 如果当前叶子节点的CF节点个数小于阈值L,则创建一个新的CF节点,放入新样本,将新的CF节点放入这个叶子节点,更新路径上所有的CF三元组,插入结束。否则转入4。
4.将当前叶子节点划分为两个新叶子节点,选择旧叶子节点中所有CF元组里超球体距离最远的两个CF元组,分布作为两个新叶子节点的第一个CF节点。将其他元组和新样本元组按照距离远近原则放入对应的叶子节点。依次向上检查父节点是否也要分裂,如果需要按和叶子节点分裂方式相同。
(3) BIRCH算法
其实将所有的训练集样本建立了CF Tree,一个基本的BIRCH算法就完成了,对应的输出就是若干个CF节点,每个节点里的样本点就是一个聚类的簇。也就是说BIRCH算法的主要过程,就是建立CF Tree的过程。
真实的BIRCH算法除了建立CF Tree来聚类,还有一些可选的算法步骤:
1) 将所有的样本依次读入,在内存中建立一颗CF Tree, 建立的方法参考上一节。
2)(可选)将第一步建立的CF Tree进行筛选,去除一些异常CF节点,这些节点一般里面的样本点很少。对于一些超球体距离非常近的元组进行合并
3)(可选)利用其它的一些聚类算法比如K-Means对所有的CF元组进行聚类,得到一颗比较好的CF Tree.这一步的主要目的是消除由于样本读入顺序导致的不合理的树结构,以及一些由于节点CF个数限制导致的树结构分裂。
4)(可选)利用第三步生成的CF Tree的所有CF节点的质心,作为初始质心点,对所有的样本点按距离远近进行聚类。这样进一步减少了由于CF Tree的一些限制导致的聚类不合理的情况。
从上面可以看出,BIRCH算法的关键就是步骤1,也就是CF Tree的生成,其他步骤都是为了优化最后的聚类结果。
(4) BIRCH算法小结
BIRCH算法可以不用输入类别数K值,这点和K-Means,Mini Batch K-Means不同。如果不输入K值,则最后的CF元组的组数即为最终的K,否则会按照输入的K值对CF元组按距离大小进行合并。
一般来说,BIRCH算法适用于样本量较大的情况,这点和Mini Batch K-Means类似,但是BIRCH适用于类别数比较大的情况,而Mini Batch K-Means一般用于类别数适中或者较少的时候。BIRCH除了聚类还可以额外做一些异常点检测和数据初步按类别规约的预处理。但是如果数据特征的维度非常大,比如大于20,则BIRCH不太适合,此时Mini Batch K-Means的表现较好。
对于调参,BIRCH要比K-Means,Mini Batch K-Means复杂,因为它需要对CF Tree的几个关键的参数进行调参,这几个参数对CF Tree的最终形式影响很大。
BIRCH算法的优缺点:
BIRCH算法的主要优点有:
1) 节约内存,所有的样本都在磁盘上,CF Tree仅仅存了CF节点和对应的指针。
2) 聚类速度快,只需要一遍扫描训练集就可以建立CF Tree,CF Tree的增删改都很快。
3) 可以识别噪音点,还可以对数据集进行初步分类的预处理
BIRCH算法的主要缺点有:
1) 由于CF Tree对每个节点的CF个数有限制,导致聚类的结果可能和真实的类别分布不同.
2) 对高维特征的数据聚类效果不好。此时可以选择Mini Batch K-Means
3) 如果数据集的分布簇不是类似于超球体,或者说不是凸的,则聚类效果不好。
5. 聚类的指标衡量
5.1均一性
一个簇中只包含一个类别的样本,则满足均一性;其实也可以认为就是正确率(每个聚簇中正确分类的样本数占该聚簇总样本数的比例和);
5.2完整性
同类别样本被归类到相同簇中,则满足完整性;每个聚簇中正确分类的样本数占类型的总样本数比例的和。
5.3 V-measure
均一性和完整性的加权平均
5.4 ARI(Adjusted Rand Index)
混淆矩阵的扩充(X表示聚合出来的类别,Y表示实际数据的类别)
数据集中可以组成的对数
这个指标不考虑使用的聚类方法,把方法当做一个黑箱,只注重结果。
ARI取值范围为[-1,1],值越大意味着聚类结果与真实情况越吻合。从广义的角度来讲,ARI衡量的是两个数据分布的吻合程度。可用于聚类算法之间的比较。
eg:
5.5 AMI(Adjusted Mutual Information)调整互信息
Q: 以上的评价指标都需要知道实际数据的标签,但是聚类算法本来就是无监督的学习方法,是不知道标签的。如果知道标签,直接用有监督的分类算法了。怎样得到Y?
5.6 轮廓系数(Silhouette)
Silhouette系数是对聚类结果有效性的解释和验证。该指标不用事先知道样本的类别。