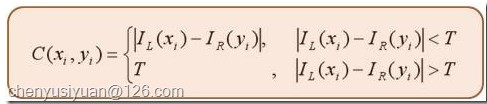四、双目匹配与视差计算

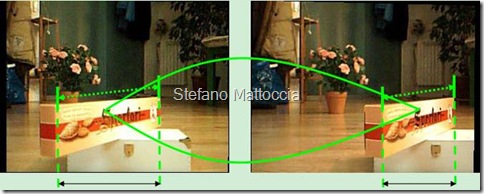
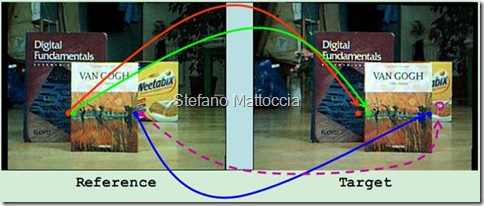
立体匹配主要是通过找出每对图像间的对应关系，根据三角测量原理，得到视差图；在获得了视差信息后，根据投影模型很容易地可以得到原始图像的深度信息和三维信息。立体匹配技术被普遍认为是立体视觉中最困难也是最关键的问题，主要是以下因素的影响：

（1） 光学失真和噪声（亮度、色调、饱和度等失衡）

（2） 平滑表面的镜面反射

（3） 投影缩减（Foreshortening）

（4） 透视失真（Perspective distortions）

（5） 低纹理（Low texture）

（6） 重复纹理（Repetitive/ambiguous patterns）

（7） 透明物体

（8） 重叠和非连续

目前立体匹配算法是计算机视觉中的一个难点和热点，算法很多，但是一般的步骤是：

A、匹配代价计算

匹配代价计算是整个立体匹配算法的基础，实际是对不同视差下进行灰度相似性测量。常见的方法有灰度差的平方SD（squared intensity differences），灰度差的绝对值AD（absolute intensity differences）等。另外，在求原始匹配代价时可以设定一个上限值，来减弱叠加过程中的误匹配的影响。以AD法求匹配代价为例，可用下式进行计算，其中T为设定的阈值。

图18

B、 匹配代价叠加

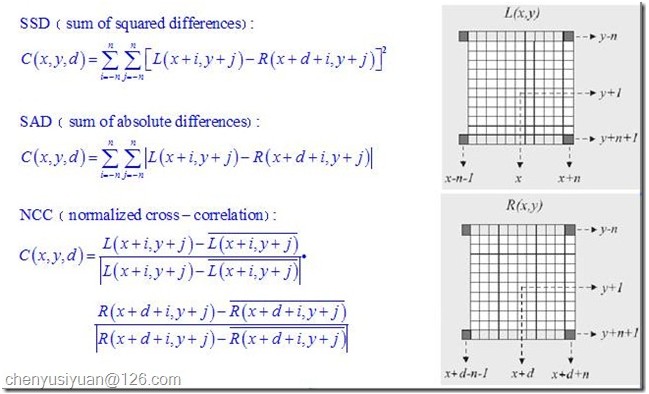
一般来说，全局算法基于原始匹配代价进行后续算法计算。而区域算法则需要通过窗口叠加来增强匹配代价的可靠性，根据原始匹配代价不同，可分为：

图19

C、 视差获取

对于区域算法来说，在完成匹配代价的叠加以后，视差的获取就很容易了，只需在一定范围内选取叠加匹配代价最优的点（SAD和SSD取最小值，NCC取最大值）作为对应匹配点，如胜者为王算法WTA（Winner-take-all）。而全局算法则直接对原始匹配代价进行处理，一般会先给出一个能量评价函数，然后通过不同的优化算法来求得能量的最小值，同时每个点的视差值也就计算出来了。

D、视差细化（亚像素级）

大多数立体匹配算法计算出来的视差都是一些离散的特定整数值，可满足一般应用的精度要求。但在一些精度要求比较高的场合，如精确的三维重构中，就需要在初始视差获取后采用一些措施对视差进行细化，如匹配代价的曲线拟合、图像滤波、图像分割等。

有关立体匹配的介绍和常见匹配算法的比较，推荐大家看看Stefano Mattoccia 的讲义 Stereo Vision: algorithms and applications，190页的ppt，讲