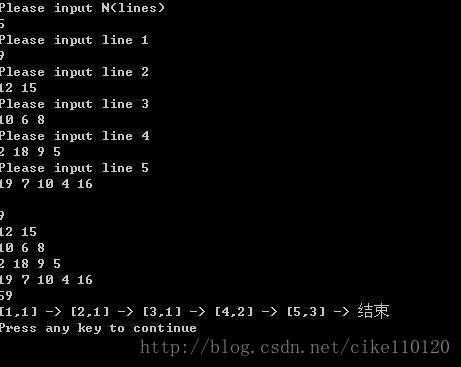
从顶点出发时到底向左走还是向右走应取决于是从左走能取到最大值还是从右走能取到最大值，

1. 只要左右两道路径上的最大值求出来了才能作出决策。
2. 同样的道理下一层的走向又要取决于再下一层上的最大值是否已经求出才能决策。
3. 这样一层一层推下去，直到倒数第二层时就非常明了。
4. 如数字2，只要选择它下面较大值的结点19前进就可以了。
5. 所以实际求解时，可从底层开始，层层递进，最后得到最大值。
6. 总结：此题是最为基础的动态规划题目，阶段、状态的划分一目了然。
7. 而决策的记录，充分体现了动态规划即“记忆化搜索”的本质。
8. 
   

数塔问题是典型的动态规划问题，我在学习了别人的设计之后感觉很简单且保持了数塔的原有结构在此做相应的修改之后在此贴出：

<span style="font-size:14px;">#include <iostream>
#define MAX 20
using namespace std;
int main()
{
	cout << "Please input N(lines)" << endl;
	//数塔的层数
	int n;
	cin >> n;

	int a[MAX+1][MAX+1][3];	//[0]用来存数，[1]参与运算，[2]表示向左(0)，还是向右(1)
	//输入数塔
	for(int i = 1; i <= n; ++i)
	{
		cout << "Please input line " << i << endl;
		for(int j = 1; j <= i; ++j)		//第i行有i个数
		{
			cin >> a[i][j][0];
			a[i][j][1] = a[i][j][0];
			a[i][j][2] = 0;
		}
	}
	//换行
	cout << endl;
	//计算
	for( i = n-1; i >= 1; --i)	//从倒数第二行开始
	{
		for(int j=1; j <= i; j++)
		{
			if (a[i+1][j][1] > a[i+1][j+1][1])	//左边大
			{
				a[i][j][2] = 0;		//选择左边
				//子父节点相加
				a[i][j][1] += a[i+1][j][1]; 
			}
			else	//右边大
			{
				a[i][j][2] = 1;		//选择右边
				a[i][j][1] += a[i+1][j+1][1];
			}
		}
	}
	
	//输出数塔
	for( i = 1; i <= n; ++i)
	{
		for(int j = 1; j <= i; ++j)
		{
			cout << a[i][j][0] << " ";
		}
		cout << endl;
	}
	//输出最大值
	cout << a[1][1][1] << endl;
	//输出路径
	int j;
	for(i = 1, j = 1; i<= n; ++i)
	{
		cout << "[" << i << "," << j << "]" << " -> ";
		j += a[i][j][2];
	}
	cout << "结束"<<endl;
	return 0;
}
</span>

以以上图的数塔数据为测试数据，程序的运行结果如下：