530.二叉搜索树的最小绝对差

题目链接/文章讲解：https://programmercarl.com/0530.%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91%E7%9A%84%E6%9C%80%E5%B0%8F%E7%BB%9D%E5%AF%B9%E5%B7%AE.html
视频讲解：https://www.bilibili.com/video/BV1DD4y11779

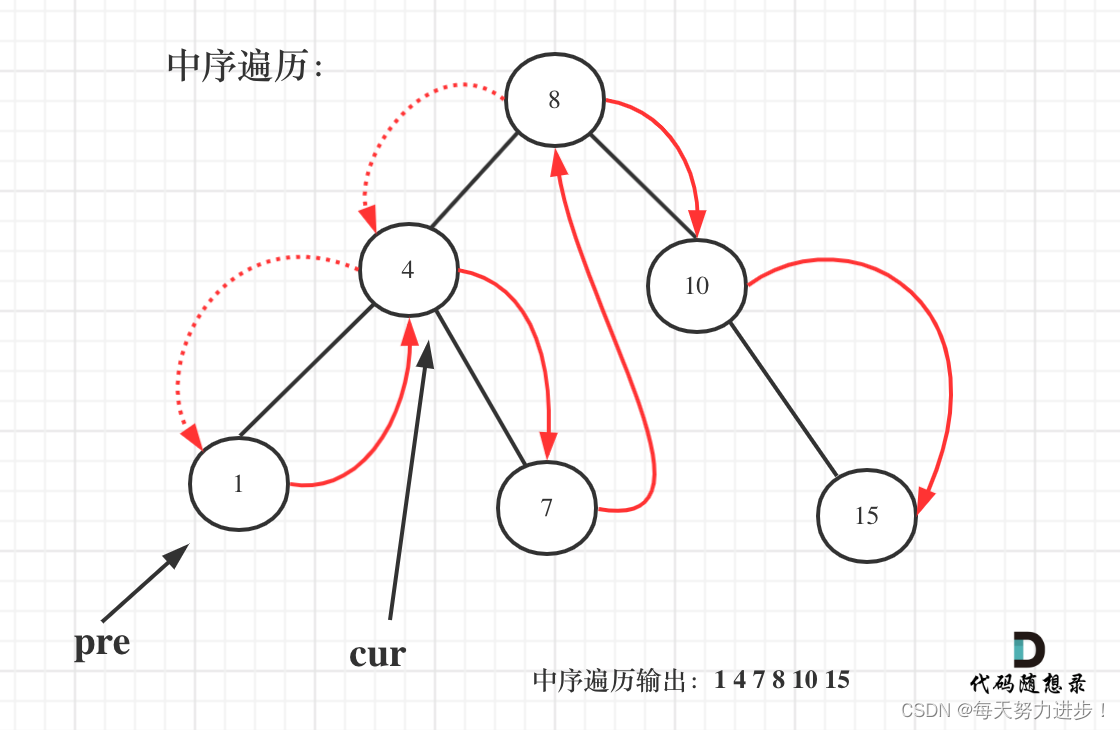
按照昨天做的二叉搜索树的特性，最简单的思路：中序遍历得到一个升序的数组，然后计算数组中相邻两个元素的最小差值

//按照昨天做的二叉搜索树的特性，最简单的思路：中序遍历得到一个升序的数组，然后计算数组中相邻两个元素的最小差值
**class Solution {
public:
    void traversal(TreeNode* root, vector<int>& result)
    {
        if(root==nullptr) return;
        traversal(root->left,result);
        result.push_back(root->val);
        traversal(root->right,result);
    }
    int getMinimumDifference(TreeNode* root) {
        vector<int> res;
        traversal(root,res);
        int min_value = 1e5;
        for(int i=1;i<res.size();i++)
        {
            if(abs(res[i-1]-res[i])<min_value)
                min_value = abs(res[i-1]-res[i]);
        }
        return min_value;
    }
};**

方法2：需要用一个pre节点记录一下cur节点的前一个节点
//利用中序遍历，左中右，“中”的时候，找相邻两节点之间的最小差值
//pre在何处更新：每一轮"中"计算完最小差值后对pre进行重新赋值
//参数返回值类型判断不符合直接在这个函数上递归，需要写一个函数traversal，目的是遍历寻找相邻两节点的差值，所以不需要返回值（result设置为全局变量）

class Solution {
    //利用中序遍历，左中右，“中”的时候，找相邻两节点之间的最小差值
    //pre在何处更新：每一轮"中"计算完最小差值后对pre进行重新赋值
    //参数返回值类型判断不符合原地递归，需要写一个遍历函数，目的是遍历寻找相邻两节点的差值，所以不需要返回值（result设置为全局变量）
private:
    int result = INT_MAX;
    TreeNode* pre = NULL;
    void traversal(TreeNode* cur)
    {
        if(cur==NULL) return;
        traversal(cur->left);
        if(pre != NULL)
            result = min(result, cur->val-pre->val);
        
        pre = cur;
        traversal(cur->right);
    }
public:
    int getMinimumDifference(TreeNode* root) {
        traversal(root);
        return result;
    }
};

501.二叉搜索树中的众数

https://programmercarl.com/0501.%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91%E4%B8%AD%E7%9A%84%E4%BC%97%E6%95%B0.html
视频讲解：https://www.bilibili.com/video/BV1fD4y117gp

1.如果看作是普通的二叉树：unordered_map存储元素以及出现的频率，然后不能对value进行排序，所以要把map转化数组即vector，再进行排序，vector里面放的也是pair<int, int>类型的数据，第一个int为元素，第二个int为出现频率。最后遍历vector取前几个频率最高的元素

//我怎么得知他出现次数最多————unordered_map记录出现次数，对值进行排序——pair数组的排序
//我怎么计算他出现的次数————排序后第一个值一定是出现次数最多的，然后把与之出现频率相同的值也保存下来

 //我怎么得知他出现次数最多————unordered_map记录出现次数，对值进行排序——pair数组的排序
 //我怎么计算他出现的次数————排序后第一个值一定是出现次数最多的，然后把与之出现频率相同的值也保存下来
class Solution {
private:
    
    void traversal(TreeNode* cur,unordered_map<int, int>& m)
    {
        if(cur==NULL) return;
        m[cur->val]++;
        traversal(cur->left,m);
        traversal(cur->right,m);
        return;
    }
    //根据出现的次数进行排序
    bool static cmp(const pair<int,int>& p1, const pair<int,int>& p2){
        return p1.second > p2.second;
    }
public:
    vector<int> findMode(TreeNode* root) {
        vector<int> res;
        if(root==NULL) return res;
        unordered_map<int,int> m;
        traversal(root,m);
        vector<pair<int,int>> vec(m.begin(),m.end());
        //排序
        sort(vec.begin(),vec.end(),cmp);
        res.push_back(vec[0].first);   //一对pair前者first,后者second
        for(int i=1;i<vec.size();i++){//太粗心了，vec的长度不是res的长度
            if(vec[i].second==vec[0].second)//排序后第一个元素出现的频次最高，以0为基准
            {
                res.push_back(vec[i].first);
            }
            else
                break;
        }
        return res;
    }
};

//递归过程中，需要处理元素的，借助pre前一个节点
//比较当前计数和最大计数，当前计数：与前一个节点相同就计数加一，不同就重新设为0
//借助中序遍历递归

 //递归过程中，需要处理元素的，借助pre前一个节点，
 //比较当前计数和最大计数，当前计数：与前一个节点相同就计数加一，不同就重新设为0
 //借助中序遍历递归
class Solution {
private:
    int maxCount=0;
    int count=0;
    TreeNode* pre = NULL;
    vector<int> res;
    void traversal(TreeNode* cur)
    {
        if(cur==NULL) return;
        traversal(cur->left);
        if(pre==NULL)
            count=1;
        else if(pre->val==cur->val){ //判断如果前一个点与之相同的话，就计数加一
            count++;
        }else{
            count=1;
        }
        pre=cur;
        if(count==maxCount)
            res.push_back(cur->val);        //有一样大的，直接搞里头
        if(count>maxCount)
        {
            maxCount = count;
            res.clear(); //说明之前存的不是最大的，需要清除掉
            res.push_back(cur->val);
        }
        traversal(cur->right);
        return;
    }
    
public:
    vector<int> findMode(TreeNode* root) {
        count=0;
        maxCount=0;
        pre=NULL;
        res.clear();
        traversal(root);
        return res;
    }
};

236. 二叉树的最近公共祖先

https://programmercarl.com/0236.%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E6%9C%80%E8%BF%91%E5%85%AC%E5%85%B1%E7%A5%96%E5%85%88.html
视频讲解：https://www.bilibili.com/video/BV1jd4y1B7E2

如果递归函数有返回值，如何区分要搜索一条边，还是搜索整个树呢？

搜索一条边的写法：
if (递归函数(root->left)) return ;
if (递归函数(root->right)) return ;

搜索整个树写法：
left = 递归函数(root->left); // 左
right = 递归函数(root->right); // 右
left与right的逻辑处理; // 中

在递归函数有返回值的情况下：如果要搜索一条边，递归函数返回值不为空的时候，立刻返回，如果搜索整个树，直接用一个变量left、right接住返回值，这个left、right后序还有逻辑处理的需要，也就是后序遍历中处理中间节点的逻辑（也是回溯）。

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root==p || root==q || root==NULL) return root;
        TreeNode* left = lowestCommonAncestor(root->left,p,q);
        TreeNode* right = lowestCommonAncestor(root->right,p,q);
        if(left!=NULL && right!=NULL)
            return root;
        else if(left==NULL)
            return right;
        else
            return left;
    }
};

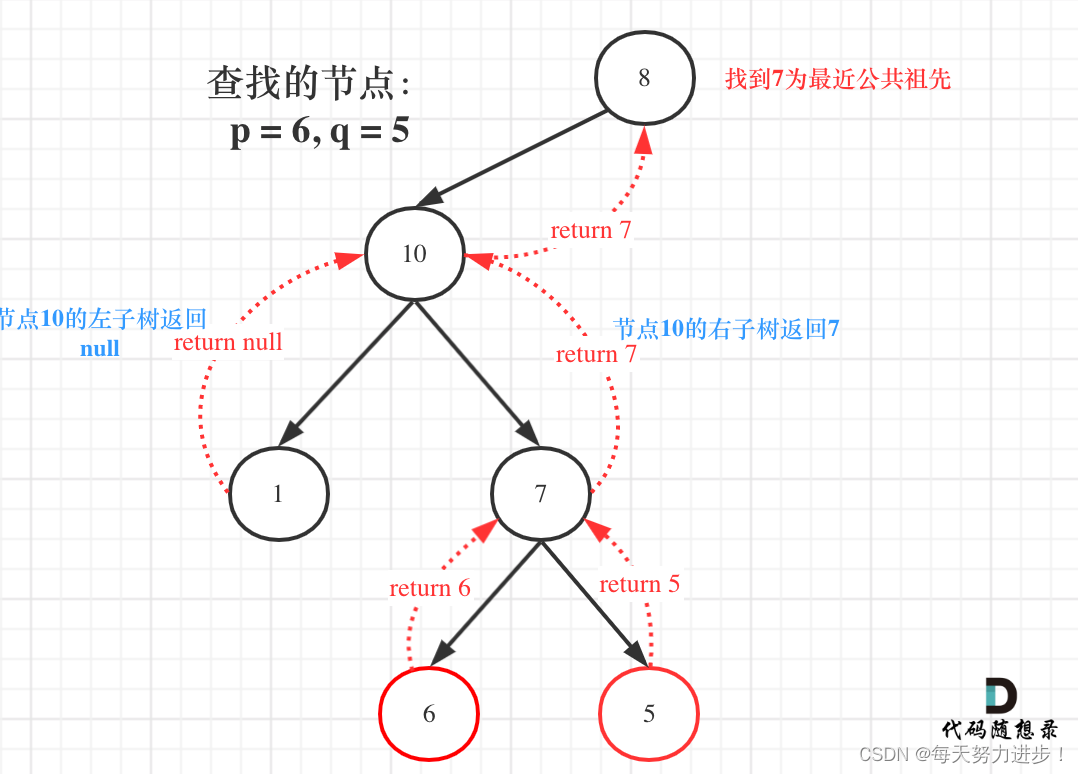
这个图已经很清晰啦！
递归终止条件：遇到p或者q或者空结点,就进行返回
遍历整个二叉树，需要left和right接返回值（如图红色 return 5这些），通过回溯把有用的信息放到一个父节点和左右孩的结构中，从而方便找到最近的公共祖先节点