416. 分割等和子集

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int sum=0;
        for(int i=0;i<nums.size();i++) {
            sum+=nums[i];
        }
        if(sum%2 !=0)
            return false;
        int target = sum/2;
        vector<int> dp(target+1,0);
        for(int i=0;i<nums.size();i++) {
            for(int j=target;j>=nums[i];j--) {
                dp[j] = max(dp[j-nums[i]]+nums[i],dp[j]);
            }
        }
        if(dp[target]==target)
            return true;
        return false;
    }
};

279. 完全平方数

class Solution {
public:
    int numSquares(int n) {
        vector<int> dp(n+1,INT_MAX);
        dp[0]=0;
        for(int i=0;i<=n;i++) {
            for(int j=1;j*j<=i;j++) {
                dp[i] = min(dp[i-j*j]+1,dp[i]);
            }
        }
        return dp[n];
    }
};

198. 打家劫舍

class Solution {
public:
    int rob(vector<int>& nums) {
        if(nums.size() == 1) {
            return nums[0];
        }
        vector<int> dp(nums.size(),0);
        dp[0]=nums[0];
        dp[1]=max(nums[0],nums[1]);
        for(int i=2;i<nums.size();i++) {
            dp[i] = max(dp[i-1],dp[i-2]+nums[i]);
        }
        return dp[nums.size()-1];
    }
};

322. 零钱兑换

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        vector<int> dp(amount+1,INT_MAX);
        dp[0]=0;
        for(int i=0;i<coins.size();i++) {
            for(int j=coins[i];j<=amount;j++) {
                if(dp[j-coins[i]]!=INT_MAX)
                    dp[j] = min(dp[j-coins[i]]+1,dp[j]);
            }
        }
        if(dp[amount]==INT_MAX)
            return -1;
        return dp[amount];
    }
};

300. 最长递增子序列

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        vector<int> dp(nums.size(),1);
        int result = 0;
        for(int i=0;i<nums.size();i++) {
            for(int j=0;j<=i;j++) {
                if(nums[j]<nums[i])
                    dp[i] = max(dp[i],dp[j]+1);
            }
            if(result < dp[i])
                result = dp[i];
        }
        return result;
    }
};

152. 乘积最大子数组

class Solution {
public:
    int maxProduct(vector<int>& nums) {
        double maxF = nums[0],minF = nums[0], ans = nums[0];
        for(int i=1;i<nums.size();i++) {
            double mx = maxF,mn = minF;
            maxF = max(mx*nums[i], max(static_cast<double>(nums[i]),mn*nums[i]));
            minF = min(mn*nums[i], min(static_cast<double>(nums[i]),mx*nums[i]));
            ans = max(maxF,ans);
        }
        return static_cast<int>(ans);
    }
};

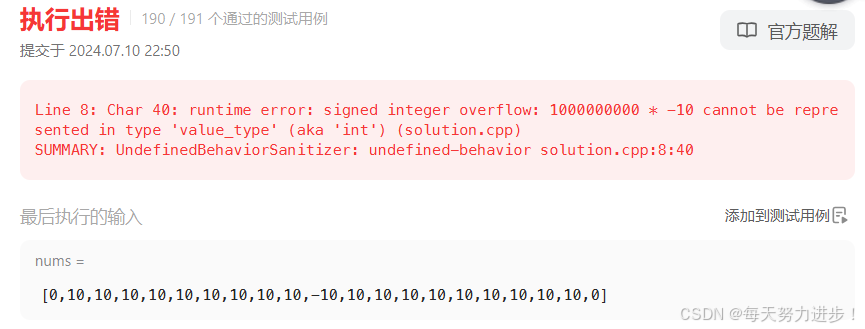
这个题的最后一个样例太恶心了…参考了大佬的题解，改为了double类型并将nums数组元素强制类型转换，最后可以通过，据说是double数值范围要更大，能够解决这个问题

class Solution {
public:
    int maxProduct(vector<int>& nums) {
        vector<vector<int>> dp(nums.size(),vector<int>(2,0));
        dp[0][0]=nums[0];
        dp[0][1]=nums[0];
        int res = dp[0][0];
        for(int i=1;i<nums.size();i++) {
            dp[i][0] = max(dp[i-1][0]*nums[i],max(nums[i],dp[i-1][1]*nums[i]));
            dp[i][1] = min(dp[i-1][1]*nums[i],min(nums[i],dp[i-1][0]*nums[i]));
            res = max(res,dp[i][0]);
        }
        return res;
    }
};