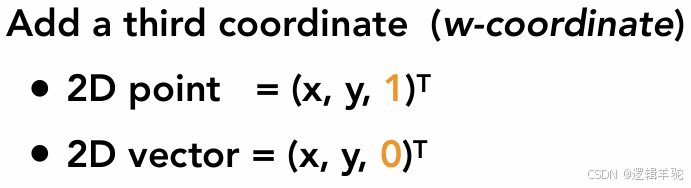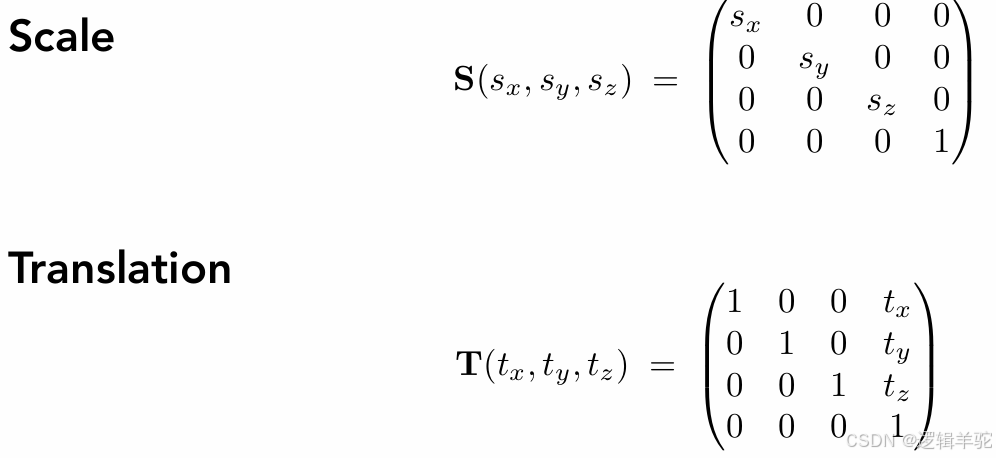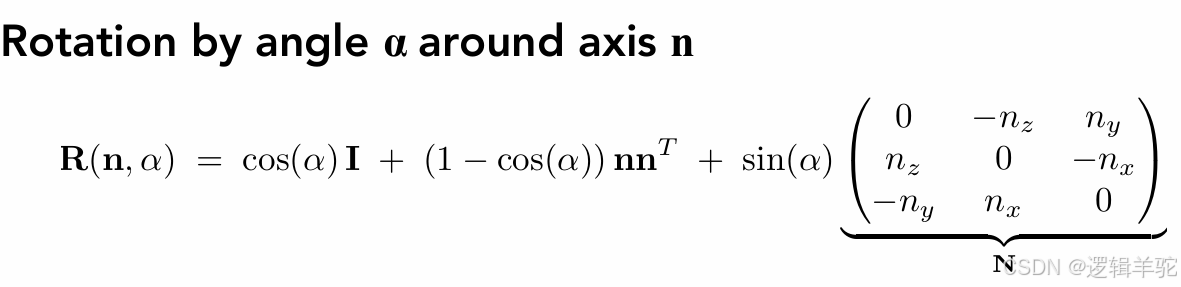理论部分📖

        仿射变换包括缩放、平移、旋转、反射、错切，仿射变换后保持不变的性质：

• 凸性：原来是直线仿射变换后还是直线
• 共线性：若几个点变换前在一条线上，则仿射变换后仍然在一条线上
• 平行性：若两条线变换前平行，则变换后仍然平行
• 共线比例不变性：变换前一条线上两条线段的比例，在变换后比例不变

        最基础的仿射变换就是线性变换+平移，可以写成如下形式：

        这显然不是线性的，为了把仿射变换变成线性变换，或者说统一变换矩阵的格式，重新定义2D中的点和向量，给它们增加一个维度，那么上面的仿射变换就可以用一个变换矩阵来表示。

🧐为什么点的第三维是1，而向量的第三维是0？

• 两个点做差即可得到向量。(x1,y1,1)-(x2,y2,1)=(x1-x2,y1-y2,0)
• 向量具有方向性，平移向量不改变其坐标值。tx,ty应该和0相乘
• 两个点相加是它们的中点。(x1,y1,1)+(x2,y2,1)=(x1+x2,y1+y2,2)=((x1+x2)/2,(y1+y2)/2,1)

        因此，2D的缩放、旋转、平移矩阵分别如下所示：

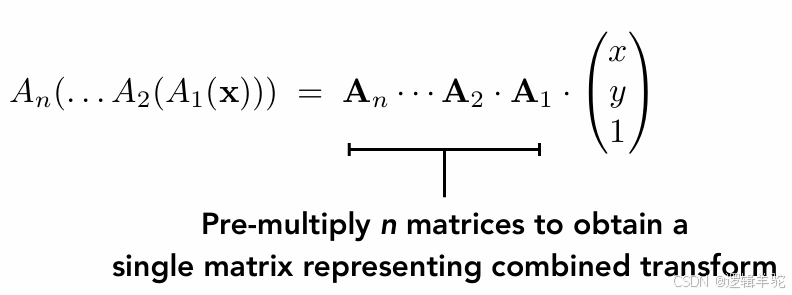
        对一个点要做什么变换就把变换矩阵依次乘在该点坐标的左侧，得到的结果即变换后的点的坐标。多个复杂的变换可以压缩成一个变换矩阵。

        ⚠️两个矩阵相乘没有交换性，故变换矩阵的顺序很重要，不同变换顺序得到的结果是不同的

        ⚠️如果要逆变换回去，就左乘这个变换矩阵的逆即可

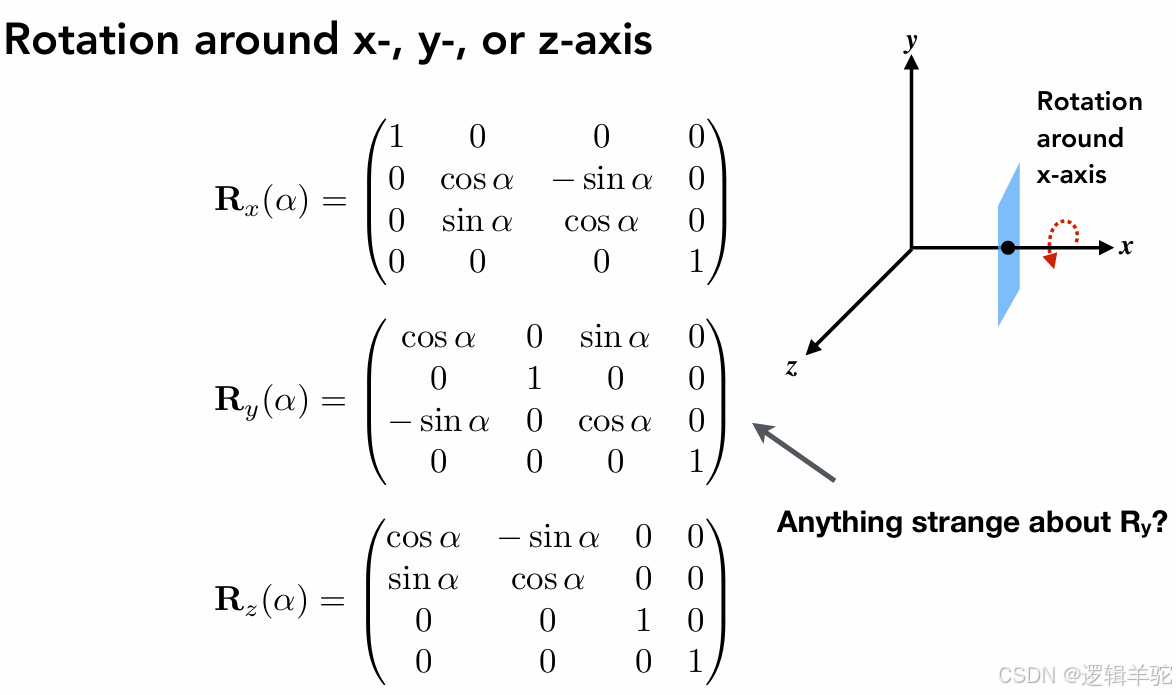
        同理，3D空间中的仿射变换如下：

       🧐旋转默认是绕原点逆时针旋转。如果要绕任意点，就要先平移到原点，旋转之后再平移回去。关于x/y/z轴旋转，x/y/z坐标不变，对应的就是Rx第一行(1,0,0,0)/Ry第二行(0,1,0,0)/Rz第三行(0,0,1,0)。剩下的用之前的2D旋转矩阵直接填入即可。这里可以形象地理解为，在3D坐标系上，过该点x坐标值做一个垂直平面，也就降维到2D平面了，自然旋转就是2D平面的旋转公式。

        🧐此处需要格外注意Ry中的负号，可以这么巧记：先写出Rx和Rz；其次，根据叉乘法则，x×z应该是朝下的，而这里y轴朝上，所以要把Ry里面的α通通换成-α，又因为cos(-α)=cosα，sin(-α)=sin(α)，所以Ry中的负号稍有点不同。

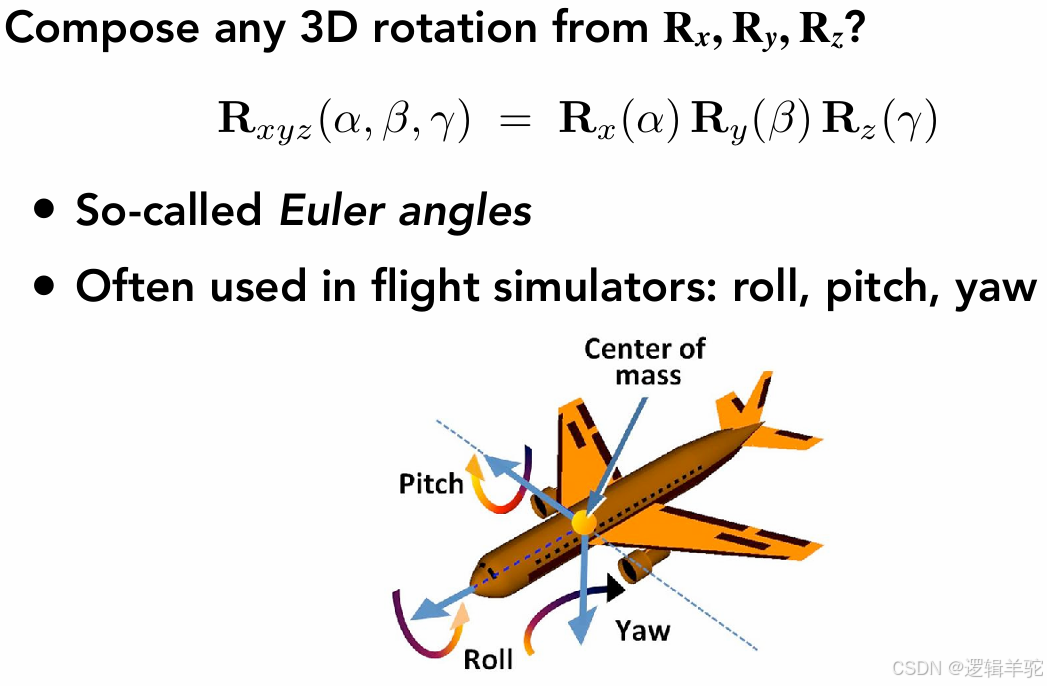
        任意旋转都可以拆解成围绕x/y/z轴按一定顺序旋转得到的结果，而围绕x/y/z轴的旋转角统称为欧拉角(Euler angles)：

• 围绕x轴的旋转运动叫做pitch，旋转角也叫俯仰角，表现为飞机头部上下运动
• 围绕y轴的旋转运动叫做yaw，旋转角也叫偏航角，表现为飞机头左右转动
• 围绕z轴的旋转运动叫做roll，旋转角也叫横滚角，表现为机翼上下倾斜

        当然，也可以围绕任意轴旋转任意角度，写成统一的变换形式的话如下所示：

Python实现代码

        附上Python实现代码——对空间中正方形的8个顶点进行操作，尽量地把解释写在备注里了，改变affine_matrix就可以得到不同的变换矩阵了。

'''
time:2024年11月11日
theme:3D坐标变换
'''
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 定义一组三维点,正方形的8个顶点
points = np.array([
    [1, 1, 1],
    [1, -1, 1],
    [-1, -1, 1],
    [-1, 1, 1],
    [1, 1, -1],
    [1, -1, -1],
    [-1, -1, -1],
    [-1, 1, -1]
])#8*3
# points.shape[0]表示点的数量，points.shape[1]表示每个点的维度
# 将点转换为齐次坐标（增加第四个维度，值为1）
ones = np.ones((points.shape[0], 1))    #生成一个全为1的列向量。np.ones(行,列)
points_h = np.hstack([points, ones])    #np.hstack将points和ones沿列方向（水平）连接，得到一个新的矩阵points_h 8*4

# 定义仿射变换矩阵（包含旋转、缩放和平移）
angle = np.radians(30)                  # 旋转角度.np.radians将角度转成弧度
scale = 1.2                             # 缩放比例
translation = np.array([2, 0, 1])       # 平移向量

# 旋转矩阵 (绕 Z 轴旋转)
x_rotation_matrix = np.array([
    [1, 0, 0, 0],
    [0, np.cos(angle), -np.sin(angle),0],
    [0, np.sin(angle), np.cos(angle) ,0],
    [0, 0, 0, 1]
])
z_rotation_matrix = np.array([
    [np.cos(angle), -np.sin(angle), 0, 0],
    [np.sin(angle), np.cos(angle), 0, 0],
    [0, 0, 1, 0],
    [0, 0, 0, 1]
])
y_rotation_matrix = np.array([
    [np.cos(angle),0,np.sin(angle), 0],
    [0,1,0, 0],
    [-np.sin(angle),0,np.cos(angle),0],
    [0, 0, 0, 1]
])

# 缩放矩阵
scale_matrix = np.array([
    [scale, 0, 0, 0],
    [0, scale, 0, 0],
    [0, 0, scale, 0],
    [0, 0, 0, 1]
])

# 平移矩阵
translation_matrix = np.array([
    [1, 0, 0, translation[0]],
    [0, 1, 0, translation[1]],
    [0, 0, 1, translation[2]],
    [0, 0, 0, 1]
])

# 合成仿射变换矩阵4*4 @用于计算计算矩阵的乘法 #先缩放再旋转再平移
# affine_matrix = translation_matrix @ z_rotation_matrix @ scale_matrix
affine_matrix = z_rotation_matrix @ translation_matrix
# 应用仿射变换 points_h一行是一个点的齐次坐标，转置变成列之后才符合我们之前的公式
transformed_points_h = (affine_matrix @ points_h.T).T
transformed_points = transformed_points_h[:, :3]    #每个点只取前三列

# 绘制原始点和变换后的点
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# 绘制原始点
ax.scatter(points[:, 0], points[:, 1], points[:, 2], color='blue', label='Original Points')
# 绘制变换后的点
ax.scatter(transformed_points[:, 0], transformed_points[:, 1], transformed_points[:, 2], color='red', label='Transformed Points')
# 设置图例和标签
ax.legend()
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
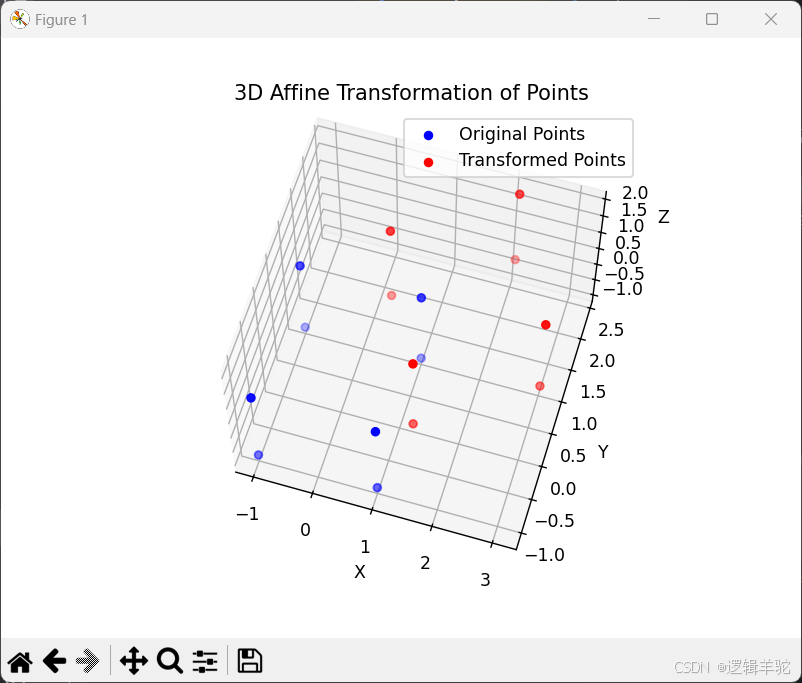
ax.set_title('3D Affine Transformation of Points')
plt.show()

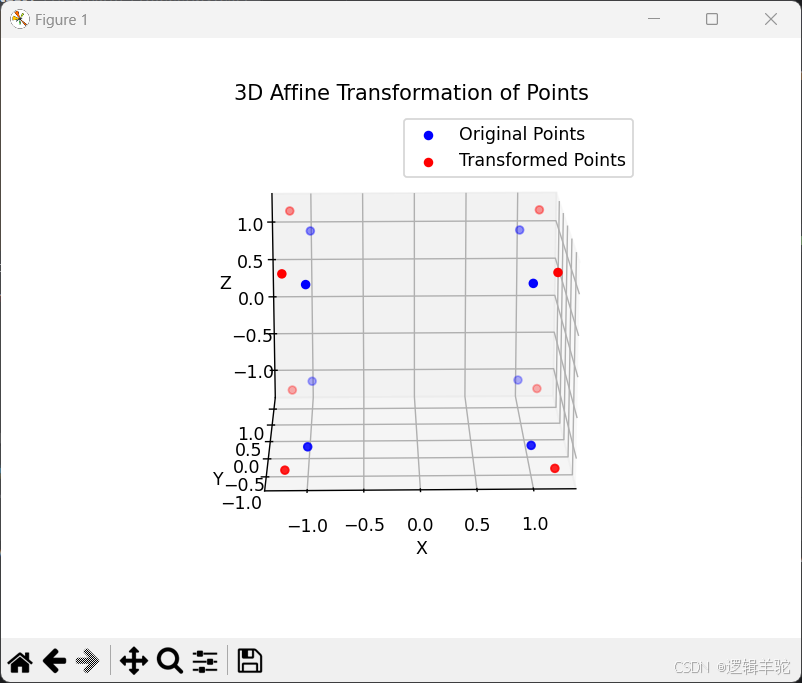
缩放1.2倍、平移(2,0,1)的效果依次如图：

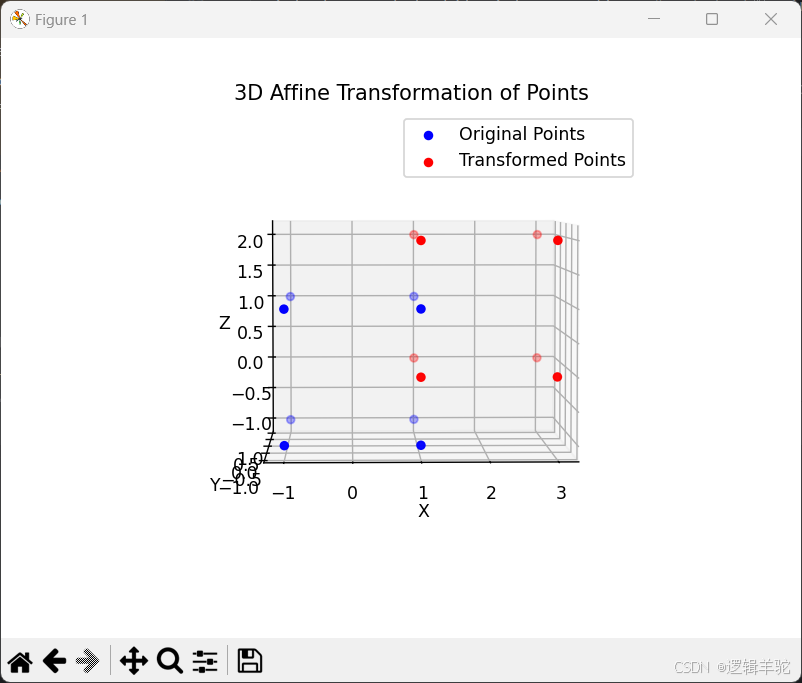
绕z轴逆时针旋转30°再缩放的效果：

这里顺便提一下，关于Python库安装遇到的一个问题，报错信息如下所示：

错误原因：不能使用代理去下载⛓️‍💥🪜

解决办法：电脑设置→网络和Internet→代理→关闭，即可成功下载

学习课程：闫令琪老师的GAMES101 现代计算机图形学入门Lecture 04 Transformation Cont._哔哩哔哩_bilibili

如果有任何不足或问题，都欢迎大家在评论区留言或私信我，非常期待和大家共同进步✌