Bootstrap

python源码剖析—— python中的字典对象

1. 散列表概述

C++的 STL 中的 map 就是一种关联容器,map 的实现基于 RB-tree(红黑树)，理论上,其搜索的复杂度为 O(logN)。Python 中同样提供关联式容器,即 PyDictObject 对象。与 map 不同的是,PyDictObject 对搜索的效率要求及其苛刻,这也是因为 PyDictObject 在 Python 本身的实现中被大量地采用,比如会通过 PyDictObject 来建立符号表。因此,PyDictObject 采用了散列表(hashtable)。理论上,在最优情况下,散列表能提供 O(1)复杂度的搜索效率。
有很多种方法可以用来解决产生的散列冲突,比如说开链法,这是 SGI STL 中的 hash table 所采用的方法;而 Python 中所采用的是另一种方法,即开放定址法。当产生散列冲突时, Python 会通过一个二次探测函数,计算下一个候选位置,如果这个位置可用,则可将待插入元素放到这个位置，如果不行将继续探测。

2. PyDictObject

2.1 关联容器的entry

在此后的描述中,我们将把关联容器中的一个(键,值)元素对称为一个 entry。

[dictobject.h]
typedef struct {
	long ma_hash;
	 /* cached hash code of ma_key */
	PyObject *ma_key;
	PyObject *ma_value;
} PyDictEntry;

ma_hash 域中存储的是 ma_key 的散列值,利用一个域来记录这个散列值可以避免每次查询的时候都要重新计算一遍散列值。

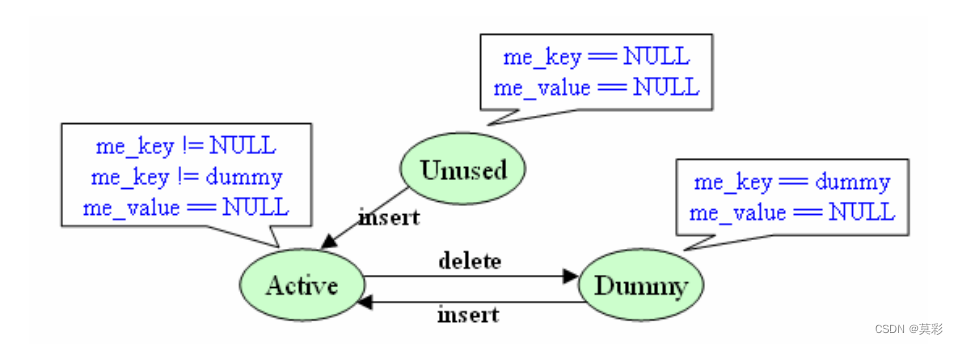
ma_key和ma_key没啥说的，就是键值对。除此之外，这两者的状态还隐含反映了当前桶的状态，即未使用、或已使用还是标记删除状态。用一张图来表示。

在这里插入图片描述

其中dummy是一个特殊的静态对象，仅仅是用于标记。在第一个 dict 对象创建时会创建该dummy对象。

dummy = PyString_FromString("<dummy key>");

2.2 关联容器的实现

[dictobject.h]
#define PyDict_MINSIZE 8
typedef struct _dictobject PyDictObject;
struct _dictobject {
	PyObject_HEAD
	int ma_fill; /* # Active + # Dummy */
	int ma_used; /* # Active */
	int ma_mask;
	PyDictEntry *ma_table;
	PyDictEntry *(*ma_lookup)(PyDictObject *mp, PyObject *key, long hash);
	PyDictEntry ma_smalltable[PyDict_MINSIZE];
};

对于PyDictObject结构体，各个字段的含义是：

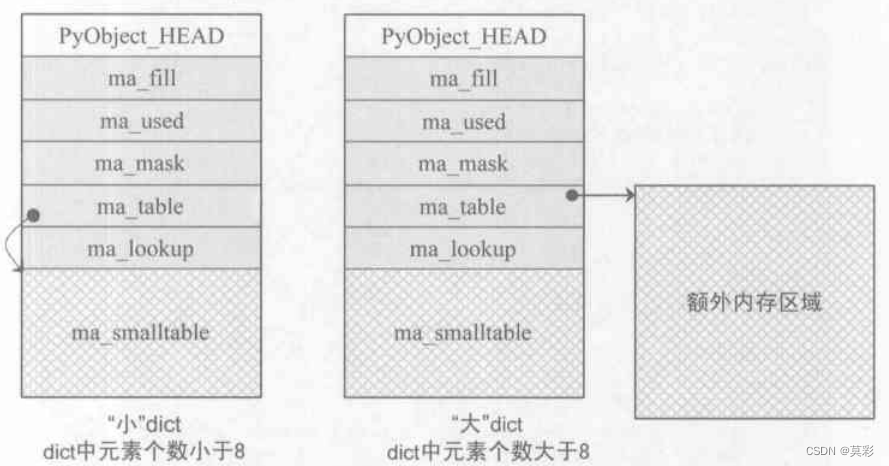
  • PyObject_HEAD : 出乎意料的，dict竟然是定长对象。我觉得一部分的原因在于小量级的字典的确是用固定长度的数组ma_smalltable来存储的。
  • ma_fill : active 加上 dummy 的 entry 数量。
  • ma_used : active 的 entry 数量。
  • ma_mask : 总的 entry 数-1，因为槽的数量始终是 2 的指数，所以这个数一定是一个所有位为 1 的变量，用于 key 的模数从而得到目标槽的索引。
  • ma_table : 指向用户存储的PyDictEntry数组。
  • ma_lookup : 哈希函数，有两种，默认是对字符串优化过的版本。
  • ma_smalltable : 小型的字典直接使用这个静态申请大小的存储空间，可能也初始化时是固定大小，PyDictObject才用的定长对象。默认情况下就是把ma_mask设置为7。

在这里插入图片描述

3. PyDictObject 的创建和维护

3.1 PyDictObject对象创建

[dictobject.c]
typedef PyDictEntry dictentry;
typedef PyDictObject dictobject;

// 缓冲池相关
#define MAXFREEDICTS 80
static PyDictObject *free_dicts[MAXFREEDICTS];
static int num_free_dicts = 0;

#define INIT_NONZERO_DICT_SLOTS(mp) do { \
	(mp)->ma_table = (mp)->ma_smalltable; \
	(mp)->ma_mask = PyDict_MINSIZE - 1; \
} while(0)

// 初始化 PyDictObject
#define EMPTY_TO_MINSIZE(mp) do { \
	memset((mp)->ma_smalltable, 0,sizeof((mp)->ma_smalltable)); \
	(mp)->ma_used = (mp)->ma_fill = 0; \
	INIT_NONZERO_DICT_SLOTS(mp); \
} while(0)

PyObject* PyDict_New(void)
{
	register dictobject *mp;
	if (dummy == NULL) {
    	/* Auto-initialize dummy */
		dummy = PyString_FromString("<dummy key>");
		if (dummy == NULL)
			return NULL;
		}
		if (num_free_dicts)
		{
			if (num_free_dicts) {
				mp = free_dicts[--num_free_dicts];
				_Py_NewReference((PyObject *)mp);
                if (mp->ma_fill) {
					EMPTY_TO_MINSIZE(mp);
				}
            }
		}
        else {
			mp = PyObject_GC_New(dictobject, &PyDict_Type);
			if (mp == NULL)
				return NULL;
			EMPTY_TO_MINSIZE(mp);
		}
		mp->ma_lookup = lookdict_string; // 设置容器的默认检索方法
		_PyObject_GC_TRACK(mp);
		return (PyObject *)mp;
	}
}

3.2 PyDicyObject中的元素搜索

这部分很重要，是理解dict的要点。

[dictobject.c]
static dictentry* lookdict_string(dictobject *mp, PyObject *key, register long hash)
{
	register int i;
	register unsigned int perturb;
	register dictentry *freeslot;
	register unsigned int mask = mp->ma_mask;
	dictentry *ep0 = mp->ma_table;
	register dictentry *ep;
    
    // 选择搜索策略
	if (!PyString_CheckExact(key)) {
		mp->ma_lookup = lookdict;
		return lookdict(mp, key, hash);
	}
	//[1] 首次寻址
	i = hash & mask;
	ep = &ep0[i];
	// if NULL or interned
    // 本来没明白为啥要直接比较指针的值，看到这个注释有些明白了，是为了判断该对象是不是被intern了，那么两个对象肯定指向同一个对象，因此指针的值相同。
	if (ep->ma_key == NULL || ep->ma_key == key)
		return ep;
	//[3] 搜索失败时返回搜索序列上的第一个dummy态的entry，由于本次是首次寻址，如果遇到了dummy，那肯定是第一个dummy，直接设置就行，但是注意后面开放寻址步骤就要判断一下之前遇没遇到dummy了。
	if (ep->ma_key == dummy)
		freeslot = ep;
	else {
		//[4] 到这里了肯定是active态了，
		if (ep->ma_hash == hash && _PyString_Eq(ep->ma_key, key))
			return ep;
		freeslot = NULL;
	}
    // 开放寻址
	/* In the loop, ma_key == dummy is by far (factor of 100s) the least likely outcome, so test for that last. */
	for (perturb = hash; ; perturb >>= PERTURB_SHIFT) {
		i = (i << 2) + i + perturb + 1;
		ep = &ep0[i & mask];
		if (ep->ma_key == NULL)
			return freeslot == NULL ? ep : freeslot;
		if (ep->ma_key == key || (ep->ma_hash == hash && ep->ma_key != dummy && _PyString_Eq(ep->ma_key, key)))
			return ep;
		if (ep->ma_key == dummy && freeslot == NULL)
			freeslot = ep;
	}
}

有几点说明：

  1. lookdict 永远都不会返回 NULL,如果在 PyDictObject 中搜索不到待查找的元素,同样会返回一个 entry，且entry处于可用状态，要么是空要么是dummy，马上就可以被赋值使用，这一点很重要，在后面的insertdict可以看到这一点是怎么被利用的。
  2. python采用的是开放寻址的方法，因此代码中也是分为两部分。第一次寻址的哈希函数，用的就是hash值对mask取余，这也是该变量被命名为mask的原因。注意到这里的hash是作为函数参数存在的，即在外部计算，因此该函数不是PyObject接口层。关于第二次的寻址策略，看后面的补充内容。
  3. 在开始时会选择搜索策略，如果是被搜索对象是字符串（而且仅仅对被搜索对象的类型有要求），就应用这个方法，否则应用lookdict这个普适版本。两者的区别在于普适版本内部有大量的捕获并处理错误的代码，还有就是对于对象的比较，字符串专用版本使用的是_PyString_Eq，而普适版本使用的是PyObject_RichCompareBool，前者仅仅比较了两个PyStringObject的长度和内容是否一致（使用strcmp的C函数），后者则会对不同的类型进行大量的处理（而且应该会调用具体类型的__eq__魔术方法）。这使得两者的效率产生差异。为什么只对字符串版本有优化呢？原因在于 Python 自身也大量使用了 PyDictObject 对象,用来维护一个作用域中变量名和变量值之间的对应关系,或是用来在为函数传递参数时维护参数名与参数值的对应关系。这些对象几乎都是用 PyStringObject 对象作为 entry 中的 key，所以 lookdict_string 的意义就显得非常重要了。
  4. 对于判断两个对象是否相等的策略一是ep->ma_hash == hash && ep->ma_key != dummy && _PyString_Eq(ep->ma_key, key)，即两个对象的哈希值要一致，且__eq__方法要满足，参考后面的 HACK 一节。另外，策略二是：ep->ma_key == key条件满足也认为两个对象相等，这个是判断intern对象的方法，两个对象指针指向一个对象，肯定要怎么相等就怎么相等。。。但是首次寻址的时候，把该条件判断放的很靠前，应该也是出于注释里面的原因“大部分对象在首次寻址的时候都可以找到”。实际上这两条策略分别对应值相等和引用相等，而且引用相等的计算消耗更小，因此先判断。
  5. lookdict方法不展开说了，关键在于理解第四条的判断一致的条件。除此之外就是多了大量的类型安全和捕获错误的代码。

3.3 插入

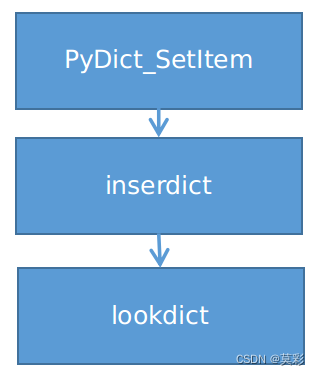
PyDictObject 对象中元素的插入动作建立在搜索的基础之上，理解了搜索操作，插入操作就是在此基础上的函数调用、调整指针和引用计数。

[dictobject.c]
static void insertdict(register dictobject *mp, PyObject *key, long hash, PyObject *value)
{
	PyObject *old_value;
	register dictentry *ep;
	ep = mp->ma_lookup(mp, key, hash);
	//[1] 搜索成功
	if (ep->me_value != NULL) {
		old_value = ep->me_value;
		ep->me_value = value;
		Py_DECREF(old_value); /* which **CAN** re-enter */
		Py_DECREF(key);
	}
	//[2] 搜索失败，得到一个可以使用的空槽
	else {
		if (ep->me_key == NULL) // UNUSED 态
			mp->ma_fill++;
		else // DUMMY 态
			Py_DECREF(ep->me_key);
		ep->me_key = key;
		ep->me_hash = hash;
		ep->me_value = value;
		mp->ma_used++;
	}
}

注意像前面说的一样，搜索失败后lookdict返回一个可以直接使用的槽。是成功还是失败，看槽的value字段就行，然后失败状态还要看区分两种状态，看代码就行，很简单。然而看函数名insertdict，还不是PyDict层的接口代码，而且lookdict需要的hash参数也不是在这里计算的，因此接着往上看一层。

[dictobject.c]
int PyDict_SetItem(register PyObject *op, PyObject *key, PyObject *value)
{
	register dictobject *mp;
	register long hash;
	register int n_used;
	mp = (dictobject *)op;
	//计算 hash 值
	if (PyString_CheckExact(key)) {
		hash = ((PyStringObject *)key)->ob_shash;
		if (hash == -1)
			hash = PyObject_Hash(key);
	}
	else {
		hash = PyObject_Hash(key);
		if (hash == -1)
			return -1;
	}
	n_used = mp->ma_used; // 插入前的used值
	Py_INCREF(value);
	Py_INCREF(key);
	insertdict(mp, key, hash, value);
	if (!(mp->ma_used > n_used && mp->ma_fill*3 >= (mp->ma_mask+1)*2))
		return 0;
	return dictresize(mp, mp->ma_used*(mp->ma_used>50000 ? 2 : 4));
}

看到这里稍微放心了，函数名没错了，看参数也没错了，应该就是PyDictObject提供的C的COL层的接口。然后看这段代码干了什么，首先找到了悬而未决的hash的计算：既然是对PyStringObject类型有优待，讲PyStringObject的ob_shash缓存字段这里也用上了用场。然后就是调用insertdict函数完成插入。

在这里插入图片描述

这个函数的后两行又是大有文章，首先看倒数第二行的判断语句。
首先检查used值是否增大，如果增大了，代表这次成功新增了一个active的元素，然后就计算装载率是否超过0.67，但是装载率却是用filled的值计算的，那我感觉前面应该也用filled值计算啊。。。没太明白。这个判断条件满足（注意有叹号，以为着条件满足时没有插入或者装载率不够大），就直接返回，否则进入下一行调整大小。对于较大的dict，大小变成当前使用槽的二倍（不考虑dummy，因为扩容过程中dummy态全被消除），较小的就翻四番(因为翻番是在used变量的基础上，因此不一定是2的整数次幂，因此这个是不是最终的dict空间大小，dictresize内部还会对这个数扩大成最小的2的整数次幂)。这个过程是有可能缩小dict的空间的，比如used很小但是filled很大的状态。

[dictobject.c]
static int dictresize(dictobject *mp, int minused)
{
	int newsize;
	dictentry *oldtable, *newtable, *ep;
	int i;
	int is_oldtable_malloced;
	dictentry small_copy[PyDict_MINSIZE];
	//[1] 确定新的table大小
	for(newsize = PyDict_MINSIZE; newsize <= minused && newsize > 0; newsize <<= 1);
	oldtable = mp->ma_table;
	is_oldtable_malloced = oldtable != mp->ma_smalltable;
	//[2] 新的table使用静态dict空间
	if (newsize == PyDict_MINSIZE) {
		newtable = mp->ma_smalltable;
		if (newtable == oldtable) {
			if (mp->ma_fill == mp->ma_used) {
				//没有任何 Dummy 态 entry,直接返回
				return 0;
            }
			//将 oldtable 拷贝,进行备份
			assert(mp->ma_fill > mp->ma_used);
			memcpy(small_copy, oldtable,
			sizeof(small_copy));
			oldtable = small_copy;
		}
	}
    //[3] 空间比较大时，动态申请堆空间
	else {
		newtable = PyMem_NEW(dictentry, newsize);
	}
	//[4] 设置新table
	mp->ma_table = newtable;
	mp->ma_mask = newsize - 1;
	memset(newtable, 0, sizeof(dictentry) * newsize);
	mp->ma_used = 0;
	i = mp->ma_fill;
	mp->ma_fill = 0;
	for (ep = oldtable; i > 0; ep++) {
		if (ep->me_value != NULL) { /* active entry */
			--i;
			insertdict(mp, ep->me_key, ep->me_hash, ep->me_value);
		}
		else if (ep->me_key != NULL) { /* dummy entry */
			--i;
			assert(ep->me_key == dummy);
			Py_DECREF(ep->me_key);
		}
	}
    # 释放旧表动态申请的空间
	if (is_oldtable_malloced)
		PyMem_DEL(oldtable);
	return 0;
}

3.4 删除

[dictobject.c]
int PyDict_DelItem(PyObject *op, PyObject *key)
{
	register dictobject *mp;
	register long hash;
	register dictentry *ep;
	PyObject *old_value, *old_key;
	//获得 hash 值
	if (!PyString_CheckExact(key) || (hash = ((PyStringObject *) key)->ob_shash) == -1) {
		hash = PyObject_Hash(key);
		if (hash == -1)
			return -1;
	}
	//搜索 entry
	mp = (dictobject *)op;
	ep = (mp->ma_lookup)(mp, key, hash);
	//删除 entry 所维护的元素
	old_key = ep->me_key;
	Py_INCREF(dummy);
	ep->me_key = dummy;
	old_value = ep->me_value;
	ep->me_value = NULL;
	mp->ma_used--;
	Py_DECREF(old_value);
	Py_DECREF(old_key);
	return 0;
}

4. 对象缓冲池

和PyListObject对象的缓冲池机制基本一致，除了多了一个需要交还动态申请的空间的步骤，这个动态申请空间导致PyDictObject成为定长对象，因为一个对象的空间的确是确定的，不确定的地方通过指针指向动态堆空间了。PyStringObject和PyListObject对象是变长对象是因为他们的对象占的空间就是不定的。

[dictobject.c]
#define MAXFREEDICTS 80
static PyDictObject *free_dicts[MAXFREEDICTS];
static int num_free_dicts = 0;

static void dict_dealloc(register dictobject *mp)
{
	register dictentry *ep;
	int fill = mp->ma_fill;

	//调整 dict 中对象的引用计数
	for (ep = mp->ma_table; fill > 0; ep++) {
		if (ep->me_key) {
			--fill;
			Py_DECREF(ep->me_key);
			Py_XDECREF(ep->me_value);
		}
	}

	//向系统归还从堆上申请的空间
	if (mp->ma_table != mp->ma_smalltable)
		PyMem_DEL(mp->ma_table);
	//将被销毁的 PyDictObject 对象放入缓冲池
	if (num_free_dicts < MAXFREEDICTS && mp->ob_type == &PyDict_Type)
		free_dicts[num_free_dicts++] = mp;
	else
		mp->ob_type->tp_free((PyObject *)mp);
}

5. HACK PyDictObject

在这里插入图片描述
在这里插入图片描述

a={True: 'yes', 1: 'no', 1.0: 'maybe'}
print(a) // {True:'maybe'}

class AlwaysNotEquals:
    def __eq__(self, other):
        return False
    def __hash__(self):
        return id(self)
ne1 = AlwaysNotEquals()
ne2 = AlwaysNotEquals()
# 全部是False
print(ne1 == ne1)
print(ne1 == ne2)
print("hello" == ne1) # str没有实现__eq__方法，因此会调用ne1的
print(ne1 == "hello")


class AlwaysEquals:
    def __eq__(self, other):
        return True
    def __hash__(self):
        return id(self)
eq1 = AlwaysEquals()
eq2 = AlwaysEquals()
# True
print(eq1 == eq1)
print(eq1 == eq2)
print("hello" == eq1)
print(eq1 == "hello")

# PyObject_RichCompareBool会优先调用前者的__eq__方法
print(eq1 == ne1) # True
print(ne1 == eq1) # False

class SameHash:
    def __hash__(self):
        return 1
sh1 = SameHash()
sh2 = SameHash()
print(sh1 == sh2) # False

# 希望利用值相同的话，必须保证hash值相同且__eq__为真
a[eq1]="eq1"
a[eq2]="eq2"
a[sh1]="sh1"
a[sh2]="sh2"

# 同一个对象肯定保证引用相同
print(a[eq1])

6. 补充内容

在dictobject.c的源码文件的开头包含了对探测机理的详细介绍，我这里就有道翻译了一下然后把句子整理通顺直接贴上来。。。

最重要的细节是:大多数哈希方案依赖于一个“良好”的哈希函数，在模拟随机性的意义上。Python没有:它最重要的散列函数(用于字符串和int)在常见情况下是非常常规的.
>>>map(hash, (“namea”, “nameb”, “namec”, “named”))
out[1] : [-1658398457, -1658398460, -1658398459, -1658398462]
这并不一定是坏事!相反，在大小为2^i的表中，以低阶i位作为初始表索引的速度非常快，并且对于由连续ints范围索引的dicts完全没有冲突。当键是“连续的”字符串时，这几乎是正确的。所以这在一般情况下比随机行为更好，这是非常可取的。
另一方面，当发生冲突时，填充哈希表的连续片的倾向使得良好的冲突解决策略至关重要。只取哈希代码的最后一个i位也是很容易出错的:例如，将[i << 16 for i in range(20000)]视为一组键。由于int值就是它们自己的哈希值，这符合大小为2^15的命令，所以每个哈希码的最后15位都是0:它们都映射到相同的表索引。
但是迎合不寻常的情况不应该减慢通常的情况，所以我们还是取最后一点。剩下的由冲突解决方案决定。如果我们通常在第一次尝试时找到我们要找的键(结果是，我们通常是这样做的——表负载因数保持在2/3，所以概率是很稳定的)，那么保持初始的索引计算非常便宜是很有意义的。
但是为了解决不寻常的情况的同时不应该减慢通常的情况，所以我们还是取最后几位比特位作为首次探索函数。剩下的由冲突解决方案决定。如果我们通常在第一次探索时就能找到我们要找的键(结果证明，我们通常可以这样的——表负载因数保持在2/3，所以概率是很稳定的)，那么保持初始的索引计算非常简单是很有意义的。
然后二次探测函数用的是这个：j = ((5*j) + 1) mod 2**i，这里还没有考虑代码中perturb的影响，j 是新的索引，i 是mask的位数。
新的方法能确保探测到全部位置吗？
对于范围内的任何初始小于2i的j，重复该2i次生成该范围内的每个数字且只生成一次。这本身并没有多大帮助:就像线性探测一样（每次索引加1），它以固定的顺序扫描表条目。这是不好的，除了这不是我们做的唯一的事情，而且在通常的散列键是连续的情况下，这是好的。在一个非常小的示例中，不能完全清楚地说明这一点，对于大小为 8 的表，索引的顺序是:0 -> 1 -> 6 -> 7 -> 4 -> 5 -> 2 -> 3 -> 0
如果连续两个值映射到索引是5的桶，第二个元素经过开放寻址被放入索引2，而不是6，所以如果下一个值出现在映射到6，那么5的碰撞不会伤害到它。在这种情况下，线性探测是致命的，因为固定探测顺序与连续键可能到达的顺序相同。对于我们选择的函数，哈希码不太可能遵循5*j+1的递归，并且确定连续的哈希码不会。
策略的另一半是让哈希代码的其他部分发挥作用。通过将perturb初始化为完整的hash，并将递归修改为:

j = (5*j) + 1 + perturb;
perturb >>= PERTURB_SHIFT;
use j % 2**i as the next table index;

现在，探查序列(最终)取决于哈希代码中的每一个比特，而在5j+1上重复出现的伪置乱属性更有价值，因为它快速放大了不影响初始索引的比特的微小差异。请注意，因为perturb是无符号的的，如果递归执行的次数足够多，那么perturb最终会变成并且保持为0。这种情况跟非常罕见，此时递归式将变为5j+1，这将保证最终会找到一个空槽(因为5和2的指数互质，并且哈希表中肯定有空槽)。
为PERTURB_SHIFT选择一个好的值是一种平衡行为。您希望它很小，以便哈希代码的高字节在迭代中继续影响探针序列;但是你想要它很大，所以在非常糟糕的情况下，高阶哈希比特会对早期的迭代产生影响。蒂姆•彼得斯(Tim Peters ran)在实验中(在正常和病理病例中)尽可能减少总碰撞，5是“最好的”，但4和6的情况并没有明显恶化。

参考：

  1. Python源码剖析（陈孺）
  2. 关于python字典类型最疯狂的表达方式
  3. 深入 Python 字典的内部实现

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
CV视觉论文Deep learning学习笔记（一）
计算机网络9 无线网络和移动网络
封装MyBatis输出结果-简单类型，对象类型，map,resulemap,模糊查询
ssm+mysql考研刷题平台小程序 -计算机毕业设计源码13109
七月论文审稿GPT第3.2版和第3.5版：通过paper-review数据集分别微调Mistral、gemma
zabbix升级
Retrofit使用与解析
【Apache Paimon】-- 4 -- Flink 消费 kafka 数据，然后写入 paimon
JS之防抖和节流
运放9个基本电路
;