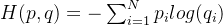在机器学习和深度学习中,交叉熵(Cross Entropy) 是一种常见的损失函数,特别适用于分类问题。尽管这个术语听起来可能有点复杂,但通过一个类比,我们可以更直观地理解它的含义和作用。
类比场景:寻找最佳路径的导游
假设你是一位导游,需要带领游客探索一片未知的森林。你事先得到了一张“概率地图”,这张地图告诉你哪些路径更可能通往目的地(例如,河流旁的小路有70%的可能性,而丛林深处的小径只有10%的可能性)。
与此同时,有另一位资深探险家,他熟悉这片森林,并知道每条路的真实概率分布。
你的任务是根据自己的“概率地图”选择路径,同时不断向资深探险家学习,希望最终你的预测(概率地图)能尽可能接近真实分布。
核心问题
如何量化你的“概率地图”与真实概率之间的差异?这正是交叉熵要解决的问题。
什么是交叉熵?
交叉熵可以看作是用一种方式衡量两种概率分布之间的“距离”。
-
第一种概率分布是你的预测概率分布,代表你认为每条路通向目的地的可能性。
-
第二种概率分布是真实的概率分布,告诉你每条路通向目的地的真实可能性。
通过计算交叉熵,你可以知道当前的“概率地图”离真实分布有多远,并根据这个信息不断调整你的预测。
数学公式
假设森林中共有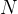
-
表示真实分布中路径
的概率。
-
表示你预测分布中路径
的概率。
交叉熵公式为:
这个公式可以分解成两部分:
-
:真实分布告诉我们哪些路径更重要。
-
:用预测分布告诉我们,你对这些路径的概率估计是否足够准确。
解释公式
-
是资深探险家的建议。他说:“路径1的可能性是70%,路径2的可能性是20%,路径3的可能性是10%。”
-
是你自己的判断。假设你认为路径1的概率是60%,路径2是30%,路径3是10%。
资深探险家会根据你的选择给出评价。如果你对高概率路径(如路径1)估计得接近真实值,那么整体评分较高;反之,如果你低估了高概率路径或高估了低概率路径,评分就会很低。
为什么负号?
负号是因为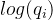
应用场景
-
分类问题: 在分类任务中,交叉熵被用来衡量模型的输出概率分布(如Softmax的输出)与真实标签之间的差异。
-
如果真实标签是“猫”(对应分类编号为1),那么
,其余
。
-
交叉熵会重点考察模型对正确分类的概率预测是否高。
-
-
语言模型: 在自然语言处理中,交叉熵用来评估语言模型生成某句话的概率与真实句子的概率分布之间的差异。
总结
通过导游和森林的类比,我们可以将交叉熵理解为一种“学习评分”机制。它帮助我们根据真实的概率分布调整预测,使得预测越来越接近真实情况。虽然理论上交叉熵可能看起来复杂,但它的本质只是量化“我们的预测和真相之间的差异”。