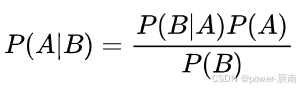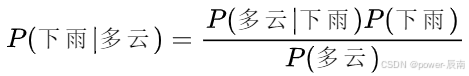一、引言
在机器学习与数据分析的广袤天地中,贝叶斯模型犹如一颗璀璨的明星,闪耀着独特的光芒,为众多领域的分类、预测等任务提供了强大的理论支撑与实用解法。然而,对于许多初涉此领域的小伙伴而言,贝叶斯模型背后的原理好似蒙上了一层神秘的面纱,让人捉摸不透。别担心!今天咱们就借助几个通俗易懂的小例子,抽丝剥茧般地详细解析贝叶斯模型的原理,助你轻松揭开这层面纱,深入领略其精妙之处。
二、贝叶斯定理:核心基石
在探究贝叶斯模型之前,必须先牢牢掌握贝叶斯定理,它可是整个贝叶斯模型大厦的基石呀。贝叶斯定理用数学公式表达如下:
这个看似简洁的公式,实则蕴含着深刻的逻辑和丰富的内涵,让我们逐一来剖析一下各部分的含义:
(一)后验概率P(A|B)
这是我们运用贝叶斯模型最想要得到的结果,它表示在事件B已经发生的条件下,事件A发生的概率。可以想象成,我们观察到了某些 “现象”(也就是事件B),然后基于这些现象去推测另一件事(事件A)发生的可能性有多大。比如说,我们看到天空乌云密布(事件B),想知道这种情况下今天下雨(事件A)的概率,这个概率P(下雨|乌云密布)就是后验概率啦。
(二)条件概率P(B|A)
它描述的是在已知事件A发生的情况下,事件B发生的概率。还是以天气为例,如果今天确定是下雨了(事件A),那么出现乌云密布(事件b)的概率就是P(乌云密布|下雨),这就是条件概率。简单来讲,它刻画了两个事件之间在特定先后顺序下的关联程度。
(三)先验概率P(A)
先验概率是指在没有考虑任何新的证据(也就是事件 )之前,我们对事件A本身发生概率的一个初始估计。比如,根据以往多年的天气统计数据,我们知道在这个季节里,下雨(事件A)的天数占总天数的比例,这就是先验概率 P(下雨)。它是基于过往经验或者已有的知识储备得到的,是我们进行后续概率推算的一个基础参照。
(四)边缘概率P(B)
边缘概率P(B)表示的是事件B发生的概率,计算它往往需要综合考虑所有可能与B相关的情况。在实际运用贝叶斯定理时,求P(B)有时候会稍微复杂一点,通常需要借助全概率公式来计算(后面会详细讲到哦)。
总之,贝叶斯定理搭建起了从先验概率、条件概率到后验概率的桥梁,让我们能够依据已有的知识和新观察到的现象,去更新对某个事件发生概率的判断,这正是贝叶斯模型的神奇之处所在呀。
三、简单例子解析原理
例 1:判断天气是否下雨
场景设定
假设我们生活在一个小镇上,想要通过一些迹象来判断每天出门时是否需要带伞,也就是判断当天是否下雨。在这里,我们设定有两个比较明显的 “迹象”(特征):天空的云量(多云或者少云)以及空气的湿度(高湿度或者低湿度)。
收集数据与概率统计
首先,我们根据过往很长一段时间的天气记录做了一个简单统计。发现总共有 100 天的数据,其中有 30 天是下雨的,70 天是不下雨的,这就是先验概率:
然后,我们又进一步统计了在下雨和不下雨的情况下,云量和湿度这两个特征出现的情况,也就是条件概率:
贝叶斯模型应用
现在,某一天早上我们起床看到天空是多云的,想通过贝叶斯模型来判断这天下雨的概率,也就是求P(下雨|多云)。
根据贝叶斯定理:
这里我们还需要先求出P(多云),根据全概率公式(它也是贝叶斯模型中常用的辅助计算方式):
可以看到,在看到天空是多云的情况下,这天下雨的概率大概是 ,还是比较有可能下雨的,那出门带上伞可能就是个明智的选择啦。
四、贝叶斯模型模型结构
一、朴素贝叶斯模型(Naive Bayes Model)
基本原理
基于贝叶斯定理,假设各个特征之间相互独立(这就是 “朴素” 的由来)。对于给定的分类问题,计算在不同类别下观测到特征向量的条件概率,再结合各类别的先验概率,通过贝叶斯定理来推算出后验概率,即给定特征向量时,样本属于各个类别的概率,最后选择概率最大的类别作为预测结果。
例如,在垃圾邮件分类中,将邮件内容拆分成一个个词语(特征),假设词语之间相互独立,统计垃圾邮件和正常邮件中每个词语出现的频率(条件概率)以及垃圾邮件和正常邮件本身出现的概率(先验概率),当收到一封新邮件时,根据邮件中出现的词语来计算它是垃圾邮件和正常邮件的概率,进而判断其类别。
特点与优势
简单高效:模型结构和计算过程相对简单,容易理解和实现,训练和预测速度较快,在处理大规模数据时效率优势明显。
对小规模数据友好:即使在数据量较少的情况下,也有可能取得不错的分类效果,不需要大量的训练样本就能进行模型训练。
可解释性较好:可以直观地看到每个特征对于不同类别概率的影响,便于理解模型决策依据,例如能明确指出哪些词汇更倾向于出现在垃圾邮件中。
应用场景
文本分类:如垃圾邮件过滤、新闻文章分类、情感分析等,通过对文本特征的提取和概率计算来判断文本所属类别。
客户分类:依据客户的年龄、消费金额、购买频次等特征对客户进行简单分类,比如区分高价值客户、低价值客户等,以便制定不同营销策略。
二、贝叶斯网络(Bayesian Network)
基本原理
也叫信念网络或有向无环图模型(DAG),通过有向无环图来表示变量之间的概率依赖关系。图中的节点代表随机变量,有向边表示变量之间的因果或依赖关系,每个节点都附有一个条件概率表(CPT),用于描述该节点在其父节点不同取值情况下的概率分布。推理过程基于贝叶斯定理,通过已知变量的信息来更新其他未知变量的概率分布,从而进行预测、诊断等任务。
例如,在医疗诊断中,节点可以表示疾病、症状、检查结果等变量,疾病节点指向症状节点体现因果关系(疾病引发症状),根据患者表现出的症状和检查结果等已知信息,利用贝叶斯网络中存储的概率关系,推算出患有某种疾病的概率。
特点与优势
能刻画复杂关系:可以准确地描述多个变量之间复杂的依赖和因果关系,更符合现实世界中事物相互关联的实际情况,相较于朴素贝叶斯,对变量关系的建模更精细。
不确定性推理:能够进行不确定性的量化和推理,不仅可以给出预测结果,还能表明结果的不确定性程度,比如在风险评估场景中,呈现风险发生概率的范围及置信度。
应用场景
医疗诊断辅助:综合考虑多种症状、疾病、检查指标等因素之间的关联,辅助医生判断病情、确定可能的疾病种类,提高诊断准确性。
故障诊断:在工业设备、软件系统等出现故障时,分析各个部件状态、故障提示信息等变量之间的关系,找出故障原因和可能的故障点,帮助维修人员快速定位问题。
三、贝叶斯线性回归(Bayesian Linear Regression)
基本原理
在传统线性回归的基础上融入贝叶斯思想。传统线性回归是寻找自变量和因变量之间的线性关系,通过最小化误差平方和等方法确定回归系数。而贝叶斯线性回归将回归系数看作是具有先验概率分布的随机变量(常见的如假设服从正态分布),基于观测到的数据(自变量和对应的因变量值),利用贝叶斯定理更新回归系数的概率分布,得到后验概率分布,然后基于此进行预测和推断,例如给出预测值及其对应的概率区间。
假设要预测房屋价格(因变量)与房屋面积、房龄等自变量的关系,贝叶斯线性回归不是确定地算出回归系数,而是先给回归系数设定先验分布,再根据收集到的房屋价格及对应特征的数据,更新系数的概率分布,进而预测某套房屋价格时能体现不确定性范围。
特点与优势
量化预测不确定性:自然地提供预测结果的不确定性信息,这在很多决策场景中非常重要,决策者可以根据不确定性程度来权衡决策风险。
融入先验知识:方便结合专家经验或历史数据等先验信息,通过合理设置回归系数的先验分布来影响模型,使模型更贴合实际情况,尤其在数据有限时优势明显。
应用场景
经济预测:预测经济指标(如 GDP 增长、通货膨胀率等)与相关影响因素(如利率、就业率等)之间的关系,同时考虑预测的不确定性,为政策制定提供参考。
环境科学:分析污染物浓度与气象因素、排放源强度等自变量的关系,对污染物浓度变化的预测附上不确定性估计,辅助环境管理决策。
四、贝叶斯逻辑回归(Bayesian Logistic Regression)
基本原理
逻辑回归原本用于处理二分类(也可扩展到多分类)问题,通过将线性组合的结果经过逻辑函数(如 Sigmoid 函数)映射到 0 到 1 之间,表示样本属于某一类别的概率。贝叶斯逻辑回归则把逻辑回归中的参数(如权重系数等)视为具有先验概率分布的随机变量,利用贝叶斯定理结合训练数据更新这些参数的概率分布,进而得到关于类别概率的后验分布,基于后验分布进行分类决策并体现结果的不确定性。
比如在判断客户是否会流失(二分类问题)时,传统逻辑回归给出一个流失概率的确定值,而贝叶斯逻辑回归给出这个概率对应的概率分布,更全面地反映分类结果的不确定性情况。
特点与优势
克服过拟合:通过引入先验分布对参数进行约束,起到正则化的作用,能有效避免模型在训练数据上过拟合,提升模型在新数据上的泛化能力,使分类结果更稳定可靠。
不确定性考量:提供分类结果的不确定性量化,对于一些关键决策场景(如医疗诊断判断疾病类型),有助于决策者综合考虑不确定性因素做出更合理的决策。
应用场景
医学诊断:判断患者是否患有某种疾病(根据症状、检验指标等特征),同时给出诊断结果的不确定性情况,辅助医生制定进一步的检查或治疗方案。
客户行为预测:预测客户对营销活动的响应情况、是否会购买特定产品、是否会流失等,为企业制定精准营销策略提供更全面的参考依据。
五、隐马尔可夫模型(Hidden Markov Model,HMM)
基本原理
用于描述含有隐含未知状态的马尔可夫过程。它假设存在一组隐藏状态序列,这些状态不能直接观测到,且隐藏状态按照马尔可夫链性质进行转移(下一时刻的隐藏状态只与当前隐藏状态有关),同时每个隐藏状态会产生相应的观测值,观测值的生成概率与隐藏状态相关。通过贝叶斯推理等方法,根据观测到的一系列观测值来推测背后的隐藏状态序列。
在语音识别中,隐藏状态可以看作是不同的语音音素,观测值就是实际听到的语音信号,每个音素产生特定语音信号有一定概率,音素之间按马尔可夫链规则转换,利用 HMM 可根据语音信号推测音素序列,进而识别出语音内容。
特点与优势
处理序列数据:特别适合处理具有顺序结构的数据,如时间序列、语音、文本等,能有效挖掘其中隐藏的模式和规律,对序列数据进行建模、分析和预测。
基于概率建模:以概率形式描述状态转移和观测生成等过程,即使存在噪声干扰或部分信息缺失,仍可通过概率推理尝试还原真实状态序列,具有较强的抗干扰能力和灵活性。
应用场景
语音识别:将语音信号转换为文字,是语音识别技术中的重要基础模型,通过推测语音背后的音素等隐藏状态来实现识别功能。
自然语言处理:如词性标注任务,推测句子中每个单词的词性(隐藏状态为词性,观测值为单词本身),还用于命名实体识别等序列标注类任务。
六、马尔可夫随机场(Markov Random Field,MRF)
基本原理
是一种无向图模型,定义了一组随机变量(节点)以及它们之间的概率依赖关系(通过无向边连接),满足马尔可夫性,即一个节点的条件概率分布只依赖于与其相邻的节点(马尔可夫毯)。通过构建变量之间的这种概率依赖模型,根据给定的数据来推断各节点的取值(如所属类别等)。
在图像分割中,把图像中的每个像素点看作随机变量,相邻像素点由于颜色、纹理等特征具有关联性,通过 MRF 构建像素间的概率依赖关系,依据图像的像素值等信息推断每个像素点属于前景还是背景等类别,实现图像分割。
特点与优势
处理空间关联数据:善于处理具有空间结构或网格结构的数据,像图像、地理空间数据等,能很好地捕捉数据中局部相关性和整体分布规律,利用关联关系进行概率建模和推断。
灵活建模:无向图结构使其在描述变量间复杂交互关系时更灵活,无需严格定义因果方向,只要确定好邻域结构和相应概率分布函数,就能对相关数据进行建模。
应用场景
图像分析:除图像分割外,还用于图像去噪(根据像素关联恢复原始图像)、纹理合成(生成具有相似纹理特征的图像)等任务,改善图像质量和生成新的图像内容。
地理信息系统:分析土地利用类型的分布(不同地块间土地利用类型存在关联)等,辅助地理空间数据的分类和理解。