人工智能之机器学习4-分类算法【培训机构学习笔记】

模型训练及测试

模型的选择：建模方法和参数都需要根据特定任务进行选择
迭代优化：将训练数据集在所选模型（算法）上进行测试，并对模型进行迭代优化
交叉验证：将数据分为训练集和测试集，使用训练集进行构建模型，使用测试集用于评估模型并进一步优化模型

分类算法中常见的指标：

1、培训班

准确率（Accuracy）= 提取出的正确样本数/总样本数
召回率（Recall） = 正确的正例样本数/样本中的正例样本数——覆盖率
精确率（Precision） = 正确的正例样本数/预测为正例的样本数
F值 = Precision * Recall * 2 / (Precision + Recall)（即F值为精准率和召回率的调和平均值）
深兰培训中，ppt质量差，字很小，如下图所示

2、个人学习：

准确率、召回率、精确率、F 值是信息检索、统计学、机器学习等领域中用于评估分类模型性能的重要指标，以下是对它们的详细理解：

准确率（Accuracy）

定义：准确率是指分类正确的样本数占总样本数的比例，反映分类器对整个数据集的分类准确程度。
计算公式： $Accuracy = \frac{TP+TN}{TP+TN+FP+FN}$ ，
TP 表示真正例（True Positive）, 即实际为正例且被分类器正确预测为正例的样本数；
TN 表示真反例（True Negative），即实际为反例且被分类器正确预测为反例的样本数；
FP 表示假正例（False Positive），即实际为反例但被分类器错误预测为正例的样本数；
FN 表示假反例（False Negative），即实际为正例但被分类器错误预测为反例的样本数。
示例：假设一个数据集包含 100 个样本，其中 60 个正例，40 个反例。分类器预测结果为 50 个正例和 50 个反例，其中真正例有 40 个，真反例有 30 个。则准确率为：70%。

精确率（Precision）

定义：精确率是指在所有被分类器预测为正例的样本中，真正例所占的比例，它反映了分类器对正例的预测准确程度。

计算公式： $Precision= \frac{TP}{TP+FP}$
示例：继续以上面的例子为例，分类器预测为正例的样本有 50 个，其中真正例有 40 个，则精确率为：80%。

召回率（Recall）

定义：召回率是指在所有实际为正例的样本中，被分类器正确预测为正例的样本所占的比例，它反映了分类器对正例的覆盖程度。
计算公式： $Recall = \frac{TP}{TP+FN}$
示例：在上述例中，实际正例 60 个，分类器正确预测的正例 40 个，则召回率为：66.7%。

F 值（F-measure）

定义：F 值是精确率和召回率的调和平均值，综合考虑了精确率和召回率，用于平衡分类器在两者之间的表现。
计算公式： $F= \frac{2\ast Precision \ast Recall}{Precision + Recall}$
示例：根据前面计算的精确率 0.8 和召回率 0.667，可得 F 值为：0.727

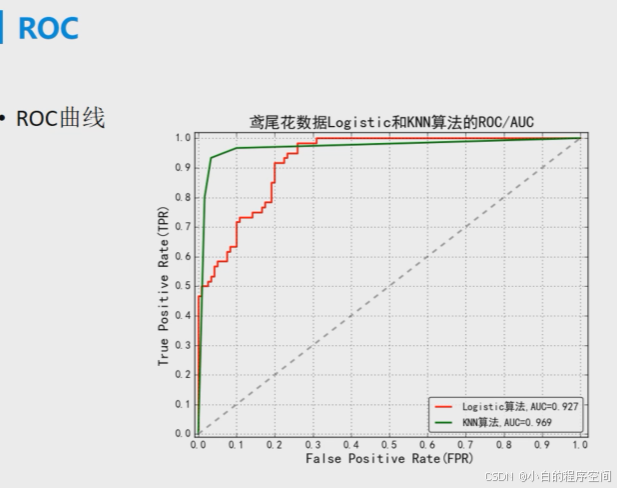
ROC

在算法领域中，ROC（Receiver Operating Characteristic）曲线是一种用于评估分类模型性能的重要工具，以下从多个方面为你详细介绍：

基本概念

ROC 曲线源于信号检测理论，它以真正例率（True Positive Rate，TPR）为纵坐标，假正例率（False Positive Rate，FPR）为横坐标绘制而成。

TPR 的计算公式为： $TPR = \frac{TP}{TP+FN}$ （召回率=被正确预测正例/所有真正的正例），其中 TP 表示真正例，即实际为正例且被模型正确预测为正例的样本数；FN 表示假反例，即实际为正例但被模型错误预测为反例的样本数。 FPR 的计算公式为： $FPR = \frac{FP}{FP+TN}$ (被错误预测反例/所有的真正的反例)，其中 FP 表示假正例，即实际为反例但被模型错误预测为正例的样本数；TN 表示真反例，即实际为反例且被模型正确预测为反例的样本数。

绘制原理

对于一个二分类模型，其预测结果通常是一个概率值，表示样本属于正类的可能性。通过设定不同的阈值，可以将概率值转换为类别预测。当阈值从大到小逐渐变化时，会得到一系列不同的 TPR 和 FPR 值，将这些值对应的点连接起来，就得到了 ROC 曲线。例如，当阈值设为 1 时，所有样本都被预测为反例，此时 TPR = 0，FPR = 0；当阈值设为 0 时，所有样本都被预测为正例，此时 TPR = 1，FPR = 1。而在阈值从 1 逐渐减小到 0 的过程中，TPR 和 FPR 会根据模型的预测结果相应地变化。

曲线特点

左上角最优：ROC 曲线越靠近左上角，说明模型的性能越好。这是因为左上角对应的是 TPR 高且 FPR 低的情况，即模型能够准确地识别出正例，同时又很少将反例误判为正例。

对角线随机：如果 ROC 曲线与对角线重合，说明模型的预测结果是随机的，等同于随机猜测。此时 TPR 等于 FPR，模型没有任何区分正例和反例的能力。

曲线下面积：ROC 曲线下的面积（Area Under the Curve，AUC）是一个重要的指标，用于量化模型的性能。AUC 的取值范围在 0.5 到 1 之间，AUC 越大，说明模型的性能越好。AUC 等于 0.5 时表示模型随机猜测，AUC 等于 1 时表示模型完全正确地预测了所有样本。

应用场景

模型比较：ROC 曲线和 AUC 可以用于比较不同分类模型的性能。在相同的数据集上，AUC 值越高的模型通常具有更好的分类能力。

阈值选择：通过观察 ROC 曲线，可以根据具体的应用需求选择合适的阈值。例如，在某些对假正例容忍度较低的场景中，可以选择 ROC 曲线上 FPR 较低的点对应的阈值，以减少误报。

特征选择：ROC 曲线还可以用于评估不同特征对模型性能的影响。通过分别使用不同的特征子集构建模型并绘制 ROC 曲线，可以确定哪些特征对提高模型性能最为关键。

小结

准确率、精确率、召回率和 F 值从不同角度评估了分类器的性能。准确率关注整体分类的准确性；精确率侧重于分类器对正例预测的准确性；召回率强调对正例的覆盖程度；F 值则综合了精确率和召回率，提供了一个更全面的评估指标。在实际应用中，需要根据具体的任务和需求来选择合适的评估指标。ROC 曲线及其相关指标为评估和比较分类模型提供了一种直观、有效的方法，帮助我们更好地理解和优化模型的性能。

思考

如何理解在某些对假正例容忍度较低的场景中，可以选择 ROC 曲线上 FPR 较低的点对应的阈值

答：在理解为何在对假正例容忍度较低的场景中，要选择 ROC 曲线上 FPR 较低的点对应的阈值时，需要从假正例的影响、ROC 曲线及阈值的关系等方面入手，以下是详细介绍：

假正例的影响

在许多实际应用场景中，假正例可能会带来较高的成本或不良后果。例如，在医疗诊断中，将健康人误诊为患有某种疾病（假正例），可能会导致患者接受不必要的进一步检查、治疗，从而产生额外的经济负担、身体痛苦以及心理压力等。
在网络安全领域，将正常的网络流量误判为恶意攻击流量（假正例），可能会触发不必要的警报，浪费安全人员的时间和精力去排查，甚至可能导致正常业务的中断。

ROC 曲线与阈值的关系

ROC 曲线是通过不断改变分类模型的阈值得到的。阈值的变化会影响模型对正例和反例的判定，从而改变真正例率（TPR）和假正例率（FPR）的值。
当阈值较高时，模型会更倾向于将样本预测为反例，此时 FPR 和 TPR 都较低；随着阈值的降低，模型越来越容易将样本预测为正例，TPR 会逐渐升高，但同时 FPR 也会随之升高。

选择 FPR 较低的点对应的阈值的原因

降低错误成本：在对假正例容忍度低的场景下，降低 FPR 意味着减少将实际为反例的样本误判为正例的数量，从而有效控制因假正例带来的各种成本和风险。比如在金融风险防控中，若将正常客户误判为高风险客户（假正例），可能会影响客户关系，甚至导致客户流失，选择低 FPR 阈值可避免这种情况。
提高预测可靠性：FPR 较低的点对应的阈值能够使模型在预测正例时更加谨慎，只有当样本具有较高的正例可能性时才将其判定为正例，从而提高正例预测的可靠性。以疾病筛查为例，只有当检测指标达到较高水平（对应较低 FPR 的阈值）时才判定为患病，可避免过多的误诊。
平衡模型性能：虽然降低阈值可以提高 TPR，使更多的正例被正确检测出来，但同时也会导致 FPR 上升。在对假正例容忍度低的情况下，优先考虑降低 FPR，在保证一定召回率的基础上，尽量减少假正例的产生，以达到更好的模型性能平衡。