并查集
作用
并查集(Disjoint Set)是一种用来解决一些等价关系问题的数据结构,它主要用于处理一些不相交集合的合并和查询操作。
-
等价关系的判断:可以用并查集来判断两个元素是否属于同一个集合,从而判断它们之间是否存在某种等价关系。
-
连通性的判断:可以用并查集来判断图中两个节点是否连通,即是否存在路径可以从一个节点到达另一个节点。
-
集合的合并与划分:可以用并查集来合并两个集合或者将一个集合划分成多个子集。
-
判断图中是否有环。
先看模板😀
定义:
const int MAX=1e5+9;
int p[MAX];//p[i]表示编号为i的人的父亲是编号为p[i]的人。MAX可以根据题目数据调整。
查询一个点的祖先:
int find(int x){
if(p[x]==x){
return x;//如果当前位置的祖先是他本身,返回他
}
return find(p[x]);//否则,就继续递归找下去
}合并两个点:
void merge(int xx,int y){
int fx=find(x),fy=find(y);//分别找到两个点的祖先
if(fx!=fy){//如果祖先不相同,说明他俩不在一个集合中,进行合并。
p[fx]=fy;//或者p[fy]=fx,都可以。
}
} 详细解释
并查集的主要是维护朋友 的朋友 的朋友 的朋友………………………………的朋友是朋友的关系。
举个例子
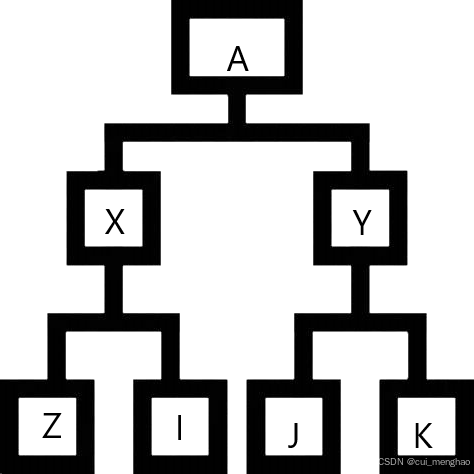
A,X,Y,Z,I,J,K分别表式他们的编号,A和X是朋友,和Y也是朋友,根据并查集的特性,X和Y也是朋友,类推下去,Z和K也是朋友。我们肉眼很容易辨认,但计算机如何实现呢?
#include<bits/stdc++.h>//万恶之源
using namespace std;
int n,m;
int x,y;
int p[1009];首先我们定义n,m分别表示人数和关系数量。x,y表示x和y是朋友关系,p[] 就是并查集了。
int find(int x){
if(p[x]==x){
return x;
}
return find(p[x]);
}
void merge(int x,int y){
int fx=find(x),fy=find(y);
if(fx!=fy){//如果在一个集合中,就不用合并了。
p[fx]=fy;
}
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++) p[i]=i;
for(int i=1;i<=m;i++){
cin>>x>>y;
merge(x,y);
}
return 0;
}先看主函数:
for(int i=1;i<=n;i++) p[i]=i;这个是什么意思呢?
据我所知,一个数组的所有元素的初始值都为0,根据p[i]表示的意思,即为并查集中所有元素的祖先都是0,再往下操作就没有意义了。所以要先把他们的祖先先设为自己,这个步骤叫初始化。
带上数据
我们先造一个数据 根据数据来解释
7 6
1 2
1 3
2 4
2 5
3 6
3 7
在初始化完成之后,我们输入x和y,分别为 1 2。
进入 merge 函数之后分别找他们的祖先,分别为 1 2 。不相同,则连接到一块(p[1]=2)。
此时的p[]:
| 第1次 | x=1 | p[] | 2 | 2 | 3 | 4 | 5 | 6 | 7 |
| y=2 | 下标 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
再次输入 x=1,y=3,同上步骤。进行操作完之后,p数组:
| 第2次 | x=1 | p[]数组 | 2 | 3 | 3 | 4 | 5 | 6 | 7 |
| y=3 | 下标2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 第2次: find(x);👇 find(y);👇 2!=3,所以p[2]=3。 | |||||||||
| 第3次 | x=2 | p[]数组 | 2 | 3 | 4 | 4 | 5 | 6 | 7 |
| y=4 | 下标 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 第3次: find(x);👇 find(y);👇 3!=4,所以p[3]=4。 | |||||||||
| 第4次 | x=2 | p[]数组 | 2 | 3 | 4 | 5 | 5 | 6 | 7 |
| y=5 | 下标 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 第4次: find(x);👇 find(y);👇 4!=5,所以p[4]=5。 | |||||||||
| 第5次 | x=3 | p[]数组 | 2 | 3 | 4 | 5 | 6 | 6 | 7 |
| y=6 | 下标 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 第5次: find(x);👇 find(y);👇 5!=6,所以p[5]=6。 | |||||||||
| 第6次 | x=3 | p[]数组 | 2 | 3 | 4 | 5 | 6 | 7 | 7 |
| y=7 | 下标 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 第6次: find(x);👇 find(y);👇 6!=7,所以p[6]=7。 | |||||||||
结合模板和数据自己画一下过程,理解会更加深刻。
总过程可概括为:
合并时,找到他们各自的祖先,合并他们的祖先,他们也就自然的在一个集合中啦。
———————————————————————————————————————————
如何得知两个人是否是朋友关系呢?
只要他在同一个集合里就一定是朋友了,而只要他俩的祖先相同,那他俩一定在同一个集合!
即:
if(find(人1)==find(人2)){
是朋友;
}else{
不是朋友;
}使用并查集判断图中是否有环
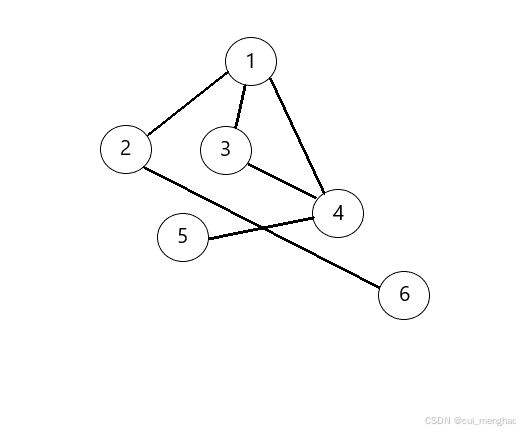
作为一个高级动物,我们一眼就能看出 1,3,4构成了一个环。
但电脑看不出来,只能由我们告诉他怎么找。
我们来跟据上图造数据:
pass:学会造数据是一项很重要的技能
6 6 (有6个节点,6条边)
1 2
1 3
1 4
2 6
3 4
4 5
那就不得不提到好用的并查集了👇
求图中环个数的代码
#include<bits/stdc++.h>
using namespace std;
int n,m;
int x,y;
int p[1009];
int ans;
int find(int x){//
return (p[x]==x)?x:find(p[x]);
}
void merge(int x,int y){
int fx=find(x),fy=find(y);
if(fx==fy){
ans++;//具体讲一下这里
}
p[fx]=fy;
}//模板
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++){
p[i]=i;
}
for(int i=1;i<=m;i++){
cin>>x>>y;
merge(x,y);
}
cout<<ans;
return 0;
}详细解释
在一个图中如果两个节点连接的时候发现已经在一个集合中了,那么再连一条边,一定能构成一个环。请读者自己画图论证。
技巧
压缩路径
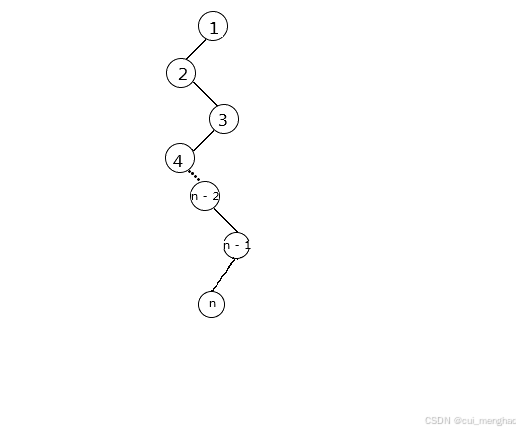
如图,如果n小一些,find()函数还能承受,但是,如果n大一些,就不行了。这时候就要用到路径压缩。
int find(int x){
if(p[x]==x){
return x;
}
return p[x]=find(p[x]);
}直接让p[i]表示他的祖先,这样就会减少循环次数。
未压缩
| n=18 | 数组 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 18 |
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
已压缩
| n=18 | 数组 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 17 | 11 | 15 | 13 | 15 | 15 | 17 | 17 | 18 | 18 |
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
步骤明显减少。
结语
关于作者对并的理解已经毫无保留了,据作者了解还有一种并查集叫种类并查集,他是用来维护敌人的敌人是朋友这种关系,感兴趣的读者可以自行搜索。