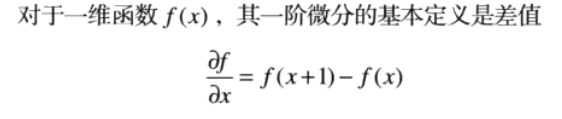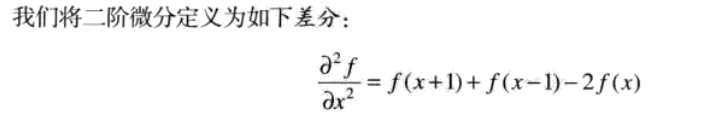前面介绍的几种滤波器都属于平滑滤波器（低通滤波器），用来平滑图像和抑制噪声的；而锐化空间滤波器恰恰相反，主要用来增强图像的突变信息，图像的细节和边缘信息。

平滑滤波器主要是使用邻域的均值（或者中值、积分）来代替模板中心的像素，消弱和邻域间的差别，以达到平滑图像和抑制噪声的目的；模糊图像，称为低通滤波器

锐化滤波器则使用邻域的微分作为算子，增大邻域间像素的差值，使图像的突变部分变的更加明显。锐化的作用是加强图像的边沿和轮廓，通常也成为高通滤波器：

一阶微分

二阶微分

大学学的高数终于排上用场了，一阶微表示函数斜率的变化，二阶导表示函数斜率曲线的斜率变化；

求导后，另一阶导等于0，可求最值；二阶导等于0，判断极值。

例子：一个扫描线上的一阶导数和二阶导数

注意：零交叉点对于边缘定位是非常有用的。

数字图像中的边缘在灰度上常常类似于斜坡过渡，如上面的例子那样，这样会导致图像的一阶微分会产生较粗的边缘，因为沿着斜坡的积分非零。

另一方面，二阶微分产生零分开的一个像素的双边缘。

由此可以得出结论，二阶微分在增强细节方面要比一阶微分好得多，这是一个适合锐化图像的理想特性。

所以我们开始主要注意二阶微分。下面，我们来考虑二维函数二阶微分的实现以及在