前言

继上一篇博客基于递归的方式学习了快速排序和归并排序
今天我们来深究快速排序，使用栈的数据结构非递归实现快排，优化快排（三路划分）
干货满满，上车

一、非递归实现快排

上篇博客基于递归实现了三个版本的快排，hoare版本，挖坑法，前后指针法
其实就是围绕基准值进行操作，不管哪一种版本，都离不开找基准值，递归得到子区间
快排的非递归版本也离不开找基准值，但是对区间进行了处理，使用到栈的数据结构

把一个大区间分成几个小区间

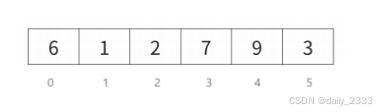
给定初始数据样例，我们正常使用前后指针的方法进行快排，找基准值

基准值，以及区间的下标

我们把0-2的区间左右下标入栈，4-5的区间下标入栈，相当于递归到子区间的操作
栈是遵循先进后出的规则，刚好和递归的区间的遍历顺序一样
每次前后指针找完基准值，就把分出来的左右区间下标入栈
但还是要注意越界的情况，比如基准值的节点在最左边或者最右边

假设基准值的下标为keyi，那么右区间就是[keyi+1，end],左区间就是[begin，keyi-1]

上图的有些区间就是不符合条件的

基本思路都叙述的差不多了，上代码

void QuickSortNonR(int* a, int left, int right)
{
	stack<int> st;   //  定义一个栈
	st.push(right);   //  这里先让右端下标入栈  因为栈是先进后出的
	st.push(left);		//    再让左端下标入栈  
	while (!st.empty())   
	{
		int begin = st.top();   //  取当前栈顶元素，也就是区间的左端 
		st.pop();
		int end = st.top();   //  取右端元素  
		st.pop();
		int prev = begin, cur = prev + 1;  // 然后就是前后指针找基准值 
		int keyi = begin;
		while (cur <= end)
		{
			if (a[cur] < a[keyi] && ++prev != cur)
			{
				swap(a[prev], a[cur]);
			}
			++cur;
		}
		swap(a[keyi], a[prev]);
		keyi = prev;         //  这里找到了基准值  
		if (keyi + 1 < end)  //  再根据基准值，分出左区间和右区间进行入栈 
		{
			st.push(end);
			st.push(keyi + 1);   //  右区间 
		}
		if (keyi - 1 > begin)
		{
			st.push(keyi - 1);
			st.push(begin);      //  左区间   
		}
	}
}

非递归版本的快速排序就完成啦

二、快排的优化版本

快排的缺陷在上篇博客和大家讲过，如果数据有序或者数据全部相同的情况，快速排序的时间复杂度可能会到O（N^2）
这里对初始基准值的确定进行优化，如果数据有序，不从第一个数据取基准值
以及在前后指针的方法上引入三路划分，对相同的数据进行处理
其次三路划分针对有大量重复数据时，效率很好，其他场景就一般，但是三路划分思路还是很价值的，有些快排思想变形体，要用划分去选数，他能保证跟key相等的数都排到中间去，三路划分的价值就体现出来了。

基准值确定的优化，使用rand函数，在区间中间随机找一个数据，比确定第一个数据要好很多，避免了一些极端情况

int randi = left + (rand() % (right - left + 1));  //  取随机数值  

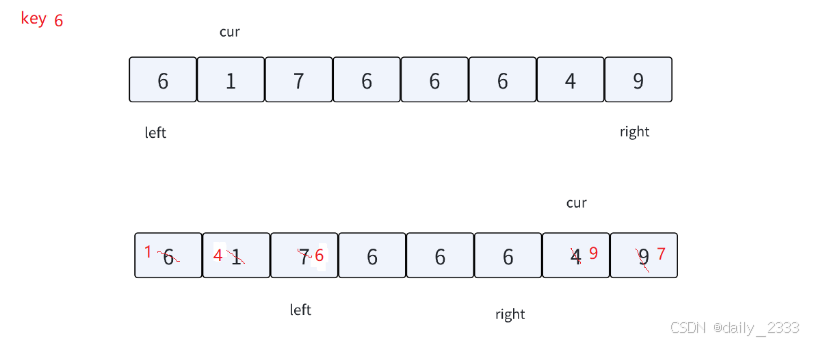
示例图：

根据上图的三路划分思路以及示例图有如下代码：

void QuickSort(int* arr, int left, int right)   //   三路划分  
{
	if (left >= right)
	{
		return;
	}
	int begin = left;
	int end = right;
	int randi = left + (rand() % (right - left + 1));  //  取随机数值作为基准值  
	swap(arr[randi], arr[left]);				//		把基准值放在最左边    
	int key = arr[left];					    //     定义key值    
	int cur = left + 1;   				//	这里类似于前后指针法  但是做了一些优化
	while (cur <= right)						//  左右同时往中间推  
	{											//  解除了中间数据相同影响性能的问题   
		if (arr[cur] < key)    //  遇到比key小的数值 交换数值  left++，cur++ 
		{
			swap(arr[cur], arr[left]);
			left++;
			cur++;
		}
		else if (arr[cur] > key)   //  遇到比key大的数据  不管right此时为什么  直接交换
		{
			swap(arr[cur], arr[right]);
			right--;      
		}
		else
		{
			cur++;
		}
	}    //   每次都看cur指定的值  如果小于key就放左边 大于right就放右边  等于就继续走  
	//  left-right区间都是相同的值  不用进一步递归  
	QuickSort(arr, begin, left - 1);    //  左区间 
	QuickSort(arr, right + 1, end);   //   右区间  
}

三、内省排序

内省排序是基于直接插入排序，堆排序，快排实现的，在合适的情景使用合适的排序方式，使排序最优化，差不多和c++里面的sort排序的底层是一样的
内省排序可以认为不受数据分布的影响，无论什么原因划分不均匀，导致递归深度太深，他就是转换堆排了，堆排不受数据分布影响。

内省排序要处理的就是递归的深度，递归层次太深的话，就转用堆排序，数据很少的话就直接使用直接插入排序，话不多说，直接上代码吧

void InsertSort(int* arr, int n)    //  直接插入排序
{
	for (int i = 0; i < n - 1; i++)
	{
		int end = i;
		int tmp = arr[end + 1];
		while (end >= 0)
		{
			if (arr[end] > tmp)
			{
				arr[end + 1] = arr[end];
				end--;
			}
			else
			{
				break;
			}
		}
		arr[end + 1] = tmp;
	}
}

void AdjustDown(int* arr, int parent, int n)   // 堆排序向下调整算法
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (child + 1 < n && arr[child] < arr[child + 1])
		{
			child++;
		}
		if (arr[child] > arr[parent])
		{
			swap(arr[child], arr[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void HeapSort(int* arr, int n)     //  堆排
{
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(arr, i, n);
	}
	int end = n - 1;
	while (end > 0)
	{
		swap(arr[0], arr[end]);
		AdjustDown(arr, 0, end);
		end--;
	}
}

void IntroSort(int* arr, int left, int right, int depth, int defaltDepth)    //  内省排序  优化排序性能   保持稳定  n*logn
{
	if (left >= right)
	{
		return;
	}
	if (right - left + 1 < 16)    //   区间大小比较小时   用插入排序  
	{
		InsertSort(arr + left, right - left + 1);
		return;
	}
	if (depth > defaltDepth)    //  当递归层次太深时   转用heap堆排序   
	{
		HeapSort(arr + left, right - left + 1);
		return;
	}
	depth++;
	int begin = left;
	int end = right;
	int randi = left + (rand() % (right - left + 1));    //  随机找基准值
	swap(arr[randi], arr[left]);
	int key = arr[left];
	int cur = left + 1;
	while (cur <= right)
	{
		if (arr[cur] < key)
		{
			swap(arr[cur], arr[left]);
			left++;
			cur++;
		}
		else if (arr[cur] > key)
		{
			swap(arr[cur], arr[right]);
			right--;
		}
		else
		{
			cur++;
		}
	}
	IntroSort(arr, begin, left - 1, depth, defaltDepth);  //  递归左右部分  
	IntroSort(arr, right + 1, end, depth, defaltDepth);
}

void QuickSort1(int* arr, int left, int right)  //   内省排序   对应数据对应处理办法  
{
	int depth = 0;
	int logn = 0;
	int n = right - left +1;
	for (int i = 1; i < n; i *= 2)
	{
		logn++;           //  递归层数   
	}
	IntroSort(arr, left, right, depth, logn * 2);
}

代码涵盖了前面所学习的各种排序算法，插入，选择，交换都涉及到了
对于快排，从最开始的hoare版本，挖坑，前后指针，都有一些些小缺陷，到现在优化到三路快排，内省排序，把时间复杂度尽量调整到了 n*logn
为什么不直接用堆排呢？？ 可能是想着多学一点知识吧 哈哈哈哈

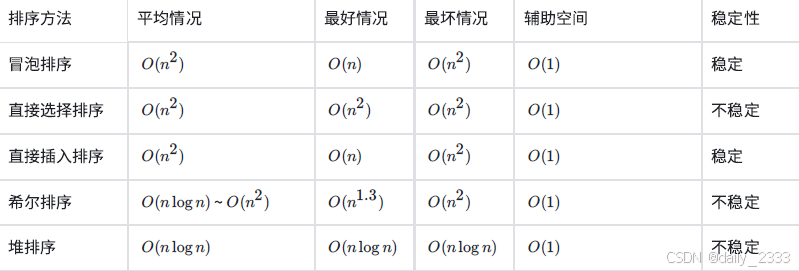
四、排序算法复杂度以及稳定性的分析

稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。
相等的元素依然按照之前的相对顺序不发生改变就是稳定的

通过这几天的学习，已经把初阶数据结构的排序算法都学完了
冒泡是具有教学意义的存在
直接一点的选择和插入都是情理之中
带有gap的直接插入变成了希尔，让直男变的有情商
快排是虽然快，但是也有发挥不好的时候
堆和归并两兄弟是发挥一直很出色，速度也很快
稳定性高，而又快速的就属归并排序

总结

本篇博客下来，快排也能一直处于稳定的时间复杂度
想想内省排序，才是对症下药，给什么样的数据，用对应克制他的排序，根据需求解决问题
优化快排的同时，有对前面的排序知识有了更深刻的认知
排序的学习就到这里了，初阶数据结构也马上结束啦，下一篇博客小编将带着大家从头到尾过一遍初阶数据结构，不要走开，小编持续更新中~~~~~

会有点难走，但总归要坚持下去