Bootstrap

算法力扣刷题记录 四十九【112. 路径总和】和【113. 路径总和ii】

前言

二叉树篇继续。
记录 四十九【112. 路径总和】和【113. 路径总和ii】

一、【112. 路径总和】题目阅读

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

示例 1：
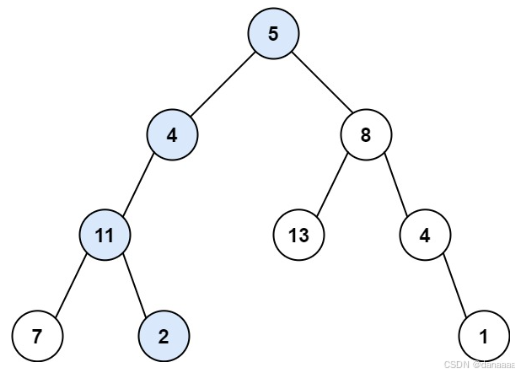
在这里插入图片描述

输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

示例 2：
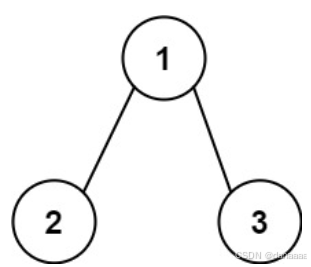
在这里插入图片描述

输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。

示例 3：

输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。

提示：

树中节点的数目在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

二、【112. 路径总和】尝试实现

题目目标是找一条路径上节点之和=targetsum。

找路径，可以想到：记录 四十六【257. 二叉树的所有路径】 就是求路径，这里在记录四十六的基础上求和判断是否相等即可。

方法【递归结合回溯】

（1）递归函数参数：需要节点TreeNode* cur；还需要path记录：vector< int > path；传递目标值：int targetsum。三个参数。
（2）递归函数返回值：bool，等于targetsum时，return true；不等于return false。
（3）终止条件：遇到叶子节点时——

  • 处理逻辑：遍历path，判断这条根节点到叶子节点的路径之和是否等于targetsum。是，return true；否则，return false。

（4）单层逻辑：

  • 先左子树的路径，如果下一层返回true，说明已经找到了，可以直接return true，接着向上层返回；如果没有：
  • 继续右子树路径，同理，如果下一层返回true，说明已经找到了，可以直接return true，接着向上层返回；
  • 左右都没能直接return true，那么该层及以下返回 false，让上一层重新遍历。
  • 回溯：path在“递”遍历时，在push_back元素，当返回时且返回false，需要pop_back弹出加入的元素。进行回溯。

（5）总结：与记录 四十六【257. 二叉树的所有路径】的区别：

  • 终止条件：处理逻辑改成求和；
  • 一遇到return true，可以直接return true。

代码实现【递归+回溯+前序遍历】

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool traversal(TreeNode* cur,vector<int>& path,int targetSum){
        path.push_back(cur->val);
        if(!cur->left &&!cur->right){//叶子节点
        	//区别一
            int sum = 0;
            for(int num:path){
                sum += num;
            }
            if(sum == targetSum) return true;
            else return false;
        }
        if(cur->left){
        	//区别二
            if(traversal(cur->left,path,targetSum)) return true;
            else path.pop_back();//回溯
        }
        if(cur->right){
            if(traversal(cur->right,path,targetSum)) return true;
            else path.pop_back();//回溯
        }
        return false;
    }
    bool hasPathSum(TreeNode* root, int targetSum) {
        vector<int> path;
        if(!root) return false;
        return traversal(root,path,targetSum);
    }
};

三、【112. 路径总和】参考学习

参考学习链接

学习内容

  1. 递归思路：直接用targetsum减去路径上的节点值，如果遇到叶子节点时，刚好减到0，说明找到；如果不等于0，说明没找到。
  2. 和二、尝试实现中的思路区别：
  • 二、中的思路是先搜集路径，用path存放，最后判断和是否相等；
  • 参考思路：不用记录路径，直接targetsum减值。
  1. 参考思路的递归实现：
  • 递归函数参数：需要节点TreeNode* cur；和此时targetsum减剩下多少值：int count ；
  • 递归函数返回值：题目给true和false的判断，所以设定bool类型；
  • 递归终止条件：叶子节点和count == 0的结合。说明要在父节点那一层先减子节点的值，当“递”到下一层可以直接判断终止条件。
  • 递归逻辑：
    • 当左子树存在，先减去左孩子的值，“递”给下一层。如果返回true，可以直接return true；注意：回溯，count减掉左孩子的值，当“回归”时，count要加回来。
    • 当右子树存在，同理。

  1. 另一种递归+回溯实现：可以对比二、中的代码实现

    /**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool traversal(TreeNode* cur,int count){
        if(!cur->left && !cur->right && count ==0) return true;//叶子节点且减到0，目标get。
        if(!cur->left && !cur->right && count != 0) return false;//路径结束，和不等。

        if(cur->left){
            //count在这一层没改变，“递给”下一层做减法
            //当返回true时，直接返回。
            if(traversal(cur->left,count-cur->left->val)) return true;
        }
        if(cur->right){//同理
            if(traversal(cur->right,count-cur->right->val)) return true;
        }
        return false;
    }
    bool hasPathSum(TreeNode* root, int targetSum) {
        if(!root) return false;
        return traversal(root,targetSum-root->val);
    }
};

  2. 迭代法思路：思路和递归一样，用栈实现。而且依然是用targetsum做减法。结合迭代遍历的模版实现：

  • 但是栈中放的元素，需要记录到它这里，targetsum减剩下多少值。所以用pair类型。
  1. 代码实现【迭代】：
    和参考中的区别：参考进行求和；下面进行减法（递归的思路）。
    /**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        stack<pair<TreeNode* ,int>> st;
        if(!root) return false;
        st.push(pair<TreeNode* ,int> (root,targetSum-root->val));
        while(!st.empty()){
            pair<TreeNode*,int> num = st.top();
            st.pop();
            if(!num.first->left && !num.first->right && num.second == 0){//叶子节点
                return true;
            }
            if(!num.first->left && !num.first->right && num.second != 0){
                continue;
            }
            if(num.first->right){//右孩子存在
                st.push(pair<TreeNode* ,int> (num.first->right,num.second-num.first->right->val));
            }
            if(num.first->left){//处理左孩子，和右孩子同理
                st.push(pair<TreeNode* ,int> (num.first->left,num.second-num.first->left->val));
            }
        }
        return false;
    }
};

四、【113. 路径总和ii】题目阅读

经过112学习，提示同类型题：【113. 路径总和ii】。那么来做下【113. 路径总和ii】。

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

示例 1：
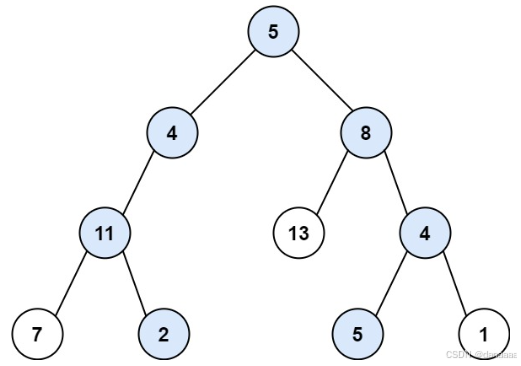
在这里插入图片描述

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

示例 2：
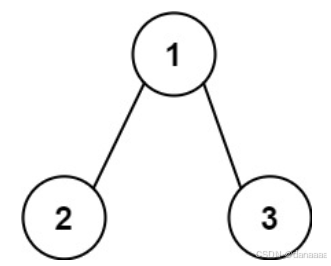
在这里插入图片描述

输入：root = [1,2,3], targetSum = 5
输出：[]

示例 3：

输入：root = [1,2], targetSum = 0
输出：[]

提示：

树中节点总数在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

五、【113. 路径总和ii】尝试实现

和【112. 路径总和】的区别：113让求出所有和等于目标值的路径。112能找到一条就可以return。

思路

  1. 求和思路：和112肯定一样。但是需要记录整个路径，所以vector< int > path在此处的作用比上面大。
  2. 递归实现，三步确定：
  • 递归参数：需要节点TreeNode* cur；需要记录路径：vector< int >& path；需要路径集合：vector<vector< int >>& result ；需要target到该节点，减剩下多少值：int count。整了4个参数。
  • 递归返回值：因为把结果都放到result中，也不需要返回什么，所以void。
  • 递归终止条件：
    • 遇到叶子节点且count==0，说明该路径要放入result。return；
    • 遇到叶子节点但count != 0，说明该路径不用放入result。直接return；
  • 递归逻辑：
    • 先把当前节点放到path中。
    • 如果左子树存在，深入遍历。“回归”的时候，path回溯，进行pop_back。
    • 如果右子树存在，深入遍历。“回归”的时候，path回溯，进行pop_back。

代码实现【递归+回溯+前序】

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void traversal(TreeNode* cur,vector<int>& path,vector<vector<int>>& result,int count){
        path.push_back(cur->val);//中
        if(!cur->left && !cur->right && count == 0){//符合条件的路径
            result.push_back(path);
            return;
        }
        if(!cur->left &&!cur->right && count != 0){//一条完整路径，但是不符合条件
            return;//不放入result，直接return
        }
        if(cur->left){
            traversal(cur->left,path,result,count-cur->left->val);
            path.pop_back();//回溯
        }
        if(cur->right){
            traversal(cur->right,path,result,count-cur->right->val);
            path.pop_back();
        }
        return;
    }
    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        vector<vector<int>> result;//返回值，路径集合
        vector<int> path;//记录路径
        if(!root) return result;
        traversal(root,path,result,targetSum-root->val);
        return result;
    }
};

六、【113. 路径总和ii】参考学习

参考学习链接

代码区别：

  • path和result的形式——参考用成员变量，不放到参数部分；五、中代码实现放到参数里。
  • 都是用targetsum减节点值，传递减剩下多少值。

总结

【112. 路径总和】和【113. 路径总和ii】：
在这里插入图片描述
（欢迎指正，转载标明出处）

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
网络通信 Posix API的原理与使用
【QT】——多线程的使用
pip版本落后，绕过pip下载python库
明尼苏达量表结果分析_⑧mmpi量表之精神病态Pd也叫病态人格，规则遵循度和创造性...
short int,int,unsigned int,long,long int,float,double等32位，64位各占几个字节的问题
web自动化测试-python+selenium+unitest
django-如何操作models.FileField数据类型
密评：网络和通信层面
为什么要使用页面缓存技术
编写程序，要求输入x的值，输出y的值。分别用（1）不嵌套的if语句（2）嵌套的if语句（3）if-else语句（4）switch语句。
;