Bootstrap

代码随想录算法训练营第十三天 | 226.翻转二叉树 101.对称二叉树 104.二叉树的最大深度 111.二叉树的最小深度

LeetCode 226.翻转二叉树：

文章链接
题目链接

思路：

遍历二叉树，将每个结点的左右子树进行翻转。因此只要是能将结点的左右子树进行翻转的遍历方式都可以

  1. 前序
# 递归
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def invertTree(self, root):
        """
        :type root: TreeNode
        :rtype: TreeNode
        """
        if not root: return root
        root.left, root.right = root.right, root.left
        self.invertTree(root.left)
        self.invertTree(root.right)
        return root

# 迭代
class Solution(object):
    def invertTree(self, root):
        stack = []
        if root: stack.append(root)
        while stack:
            cur = stack.pop()
            if cur.right: stack.append(cur.right)
            if cur.left: stack.append(cur.left)
            cur.left, cur.right = cur.right, cur.left
        return root

# 统一迭代
class Solution(object):
    def invertTree(self, root):
        stack = []
        if root: stack.append(root)
        while stack:
            cur = stack.pop()
            if cur:     # 入栈左右结点和当前结点做标记
                if cur.right: stack.append(cur.right)
                if cur.left: stack.append(cur.left)
                stack.append(cur)
                stack.append(None)
            else:   # 遇到标记处理当前结点
                cur = stack.pop()
                cur.left, cur.right = cur.right, cur.left
        return root
  1. 中序
#递归
class Solution(object):
    def invertTree(self, root):
        # 中序递归
        if not root: return root
        # 先处理左子树
        self.invertTree(root.left)
        root.left, root.right = root.right, root.left   # 交换左右结点
        # 此时的左子树是交换前的右子树，处理新左子树
        self.invertTree(root.left)
        return root

# 非统一迭代
class Solution(object):
    def invertTree(self, root):
        stack = []
        cur = root
        while cur or stack:
            if cur:
                stack.append(cur)
                cur = cur.left
            else:
                cur = stack.pop()
                cur.left, cur.right = cur.right, cur.left
                cur = cur.left
        return root
  1. 层序遍历
class Solution(object):
    def invertTree(self, root):
        queue = deque()
        if root: queue.append(root)
        while queue:
            q_size = len(queue)
            for _ in range(q_size):
                cur = queue.popleft()
                if cur.left: queue.append(cur.left)
                if cur.right: queue.append(cur.right)
                cur.left, cur.right = cur.right, cur.left
        return root

感悟：

抓住主要特点：给定结点，交换结点的左右子树

LeetCode 101.对称二叉树：

文章链接
题目链接：101.对称二叉树

思路：

  1. 层序遍历？
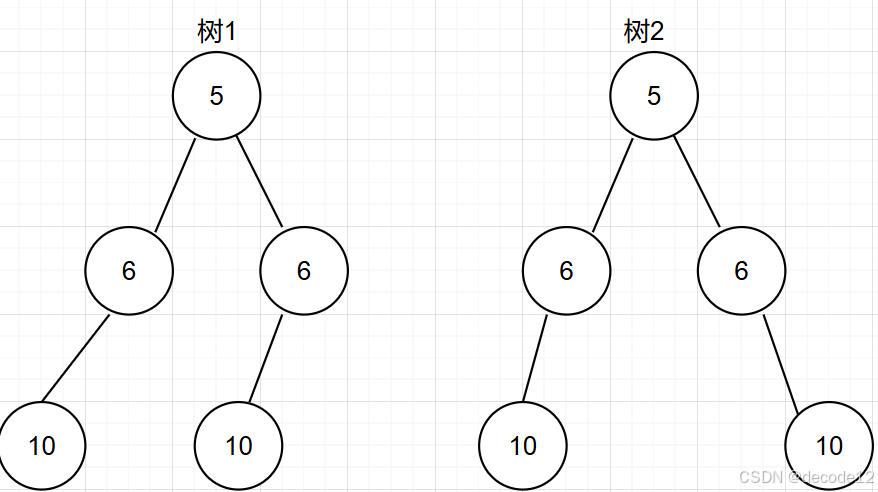
    如下图所示，两颗树的层序遍历相同，但是明显树1不是对称树，树2是对称树。但是层序遍历时使用None对二叉树进行填充，从而判断当前层是否对称时用到None。
    层序遍历的算法的修改：当前结点存在时，左右孩子结点均入队，每层使用列表保存当前层的全部结点（包括None）的值，然后判断列表是否对称
    在这里插入图片描述
from collections import deque
class Solution(object):
    def isSymmetric(self, root):
        """
        :type root: TreeNode
        :rtype: bool
        """
        if not root:
            return True
        queue = deque()
        queue.append(root.left)
        queue.append(root.right)
        while queue:
            q_size = len(queue)
            if q_size % 2 != 0:     # 剪枝
                return False
            level_c = []	# 保存的是结点的值而不是结点
            for _ in range(q_size):
                cur = queue.popleft()
                if cur:     # 不为None才入栈左右孩子
                    # cur的左右孩子均入栈（不管是否为空）
                    queue.append(cur.left)  
                    queue.append(cur.right)
                    level_c.append(cur.val)
                else:
                    level_c.append(-101)	# None对应的值不在结点值的范围内
            if level_c != level_c[::-1]:
                return False
        return True
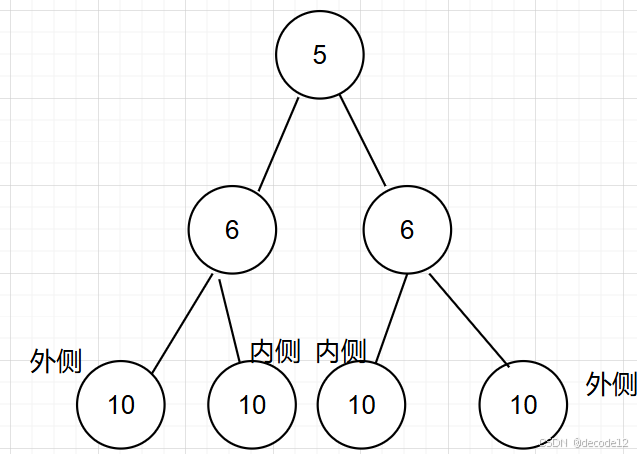
  1. 广义上的后序遍历
    判断树是否为轴对称，需要判断根的左右子树是否对称，比较左右子树的外侧是否相等、内侧是否相等，事实上是判断左子树的外侧与右子树的外侧是否相等，接着判断左子树的内侧与右子树的内侧是否相等，接着对判断结果进行汇总。
    在这里插入图片描述
  • 采用递归的方式
    ① 传入参数与返回值：需要传入左子树的判断结点和右子树的判断结点，函数返回判断结果
bool  compare(TreeNode left, TreeNode right){
}

② 边界条件（直接返回的条件）：判断left和right是否对称

# 左空右不空  || 左不空右空   false
if ((left == NULL && right != NULL) || (left != NULL && right == NULL)	return false
# 左右均为空 true
else if(left == NULL && right == NULL) return true
# 左右均不为空且值不同 false
else if(left->val != right->val)	return false

③ 正常递归下去：判断外侧是否相等，内侧是否相等，并对结果进行整理

bool outside = compare(left->left, right->right)
bool inside = compare(left->right, right->left)
bool result = outside && inside
return bool

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def isSymmetric(self, root):
        """
        :type root: TreeNode
        :rtype: bool
        """
        if not root:  
            return True
        return self.compare(root.left, root.right)
        
    def compare(self, left, right):
        # 边界条件
        if (left and not right) or (not left and right):    # 有一个为空另一个不为空
            return False
        elif not left and not right:    # 均为空
            return True
        elif left.val != right.val:     # 均不为空且值不等
            return False
        
        # 正常递归下去
        outside = self.compare(left.left, right.right)
        inside = self.compare(left.right, right.left)
        return (inside and outside)
  • 迭代方式（使用栈/队列）
    和递归的思路相同，从栈/队列中弹出两个要比较的结点，对当前结点的值进行比较后外侧结点成对、内侧结点成对入队（None也要进）
# 队列
from collections import deque
class Solution(object):
    def isSymmetric(self, root):
        if not root:  
            return True
        queue = deque()
        # 出队顺序：左右
        queue.append(root.left)
        queue.append(root.right)
        while queue:
            left = queue.popleft()
            right = queue.popleft()
            # 比较当前结点是否对称
            if not left and not right:
                continue
            elif not left or not right: # 一个为空，另一个不为空
                return False
            elif left.val != right.val: # 均不为空，且值不同
                return False
            # 均不为空且值相同，外侧结点成对、内侧结点成对入队
            queue.append(left.left)     # 外侧
            queue.append(right.right)
            queue.append(left.right)    # 内侧
            queue.append(right.left)
        return True 



# 栈
class Solution(object):
    def isSymmetric(self, root):
        if not root:
            return True
        # 弹出顺序：左右
        stack = [root.right, root.left]
        while stack:
            left = stack.pop()
            right = stack.pop()
            # 比较当前结点
            if not left and not right:  # 均为空
                continue
            elif not left or not right:     # 只有一个为空，另一个不为空
                return False
            elif left.val != right.val:     # 均不为空且值不等
                return False
            # 成对压栈结点
            stack.append(right.right)   # 外侧
            stack.append(left.left)
            stack.append(right.left)    # 内侧
            stack.append(left.right)
        return True

感悟：

内外侧进行判断，先判断当前左右结点的左右子树是否相等，再在当前结点进行整理。（层序遍历解决方法进一步需要再研究一下）

LeetCode 104.二叉树的最大深度：

文章链接
题目链接：104.二叉树的最大深度

思路：

  1. 递归后序遍历求最大深度
class Solution(object):
    def maxDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        def getdepth(node):
            if not node:
                return 0
            left_depth = getdepth(node.left)    # 左
            right_depth = getdepth(node.right)  # 右
            depth = 1 + max(left_depth, right_depth)    # 根
            return depth
        tree_depth = getdepth(root)
        return tree_depth
  1. 层序遍历求最大深度（模板）
from collections import deque
class Solution(object):
    def maxDepth(self, root):
        queue = deque()
        if root: queue.append(root)
        level = 0
        while queue:
            q_size = len(queue)
            level += 1
            for _ in range(q_size):
                cur = queue.popleft()
                if cur.left: queue.append(cur.left)
                if cur.right: queue.append(cur.right)
        return level

感悟：

求深度注意只有根节点时深度为0还是1

LeetCode 111.二叉树的最小深度：

文章链接
题目链接：111.二叉树的最小深度

思路

  1. 递归后序遍历
    需要注意深度是到叶子结点的深度，None不存在深度
class Solution(object):
    def minDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        def getDepth(node):
            if not node:
                return 0
            left_depth = getDepth(node.left)
            right_depth = getDepth(node.right)
            if node.left and not node.right:
                return left_depth + 1
            elif not node.left and node.right:
                return right_depth + 1
            else:
                depth = 1 + min(left_depth, right_depth)
                return depth
        depth = getDepth(root)
        return depth
  1. 层序遍历
    每层从左到右遍历过程中，遇到的第一个叶子结点的深度就是最小深度
from collections import deque
class Solution(object):
    def minDepth(self, root):
        queue = deque()
        if root: queue.append(root)
        min_level = 0
        while queue:
            q_size = len(queue)
            min_level += 1
            for _ in range(q_size):
                cur = queue.popleft()
                # 从左向右遍历，遇到的第一个叶子节点的层为最小深度
                if not cur.left and not cur.right: return min_level
                else:
                    if cur.left : queue.append(cur.left)
                    if cur.right: queue.append(cur.right)
        return min_level

感悟：

深度不算None结点，只算叶子结点

学习收获：

利用递归的后序遍历求解与层序遍历，二叉树需要用到遍历的题目需要首先弄清楚要用什么遍历方式

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
关于open-type
windows防火墙配置（以windows server2008为例）
weixin189基于微信小程序的高校教务管理系统设计与实现springboot含文档附源码
数据库的自我修复：实现数据故障恢复的策略与实践
FreeRTOS学习笔记——中断管理简介
叮叮书屋提交表单作业代码 web开发实验报告代码
JMeter 实战 - HTTP请求详解
VUE+Element 动态生成表单 and 动态生成校验（全网首发）
XDMA原理学习（1）——DMA技术详解
交换机堆叠和热备的区别
;