108.冗余连接:
思路
首先分析题目,给定拥有n个节点和n条边的图,其中图是在原n个节点和n - 1条无环无向图中添加一条边得到的。要求是输出多出的边。(PS:可能会有多个答案)
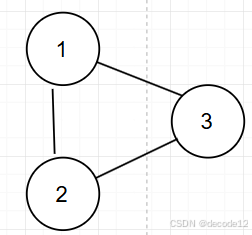
比如下图:12,13,23都是可能的答案
还是分析题目,题目可知是得到多出来的可以删除的边,而结合题目给的条件可知,多出来的边即添加时,对应的节点已经在同一个集合中(也就是成环)。
也就是用并查集添加边,当添加的边的节点已经在集合中时,该边就是需要删除的边。
"""
下面采用的是join函数增加一个返回值的情况
也可以是join没有返回值,先is_same判断是否在一个集合中,再加入集合
"""
class UnionFind():
def __init__(self, size):
self.parent = [x for x in range(size + 1)] # 节点编号从1开始
def find(self, u):
if self.parent[u] != u:
self.parent[u] = self.find(self.parent[u])
return self.parent[u]
def is_same(self, u, v):
return self.parent[u] == self.parent[v]
def join(self, u, v): # 添加v→u
root_v = self.find(v)
root_u = self.find(u)
if root_u != root_v: # 原本不存在这条路径
self.parent[root_v] = root_u
return 1
return 0 # 原本存在这条路径
def main():
n = int(input())
uf = UnionFind(n + 1)
for _ in range(n):
s, t = map(int, input().split())
if uf.join(s,t) == 0: # 原本存在这条路径
print(str(s) + ' ' + str(t))
return
if __name__ == '__main__':
main()
109.冗余连接Ⅱ:
本题比上题难得多,删除边一共有三种情况:
-
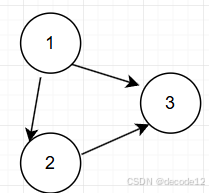
- 存在入度为2的节点,随便删除该节点上一条边(但是题目要求是多条边可以删除的话,删除后出现的边)
- 存在入度为2的节点,随便删除该节点上一条边(但是题目要求是多条边可以删除的话,删除后出现的边)
-
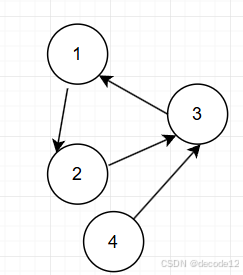
- 存在入度为2的节点,只能删除特地一条边,如下图,只能删除23这条边
- 存在入度为2的节点,只能删除特地一条边,如下图,只能删除23这条边
-
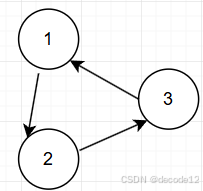
- 不存在入度为2的节点,存在环,那么删除使之成环的边即可
那么处理方式为:(需要保存边)
- 不存在入度为2的节点,存在环,那么删除使之成环的边即可
- 首先统计节点的入度
- 然后逆序保存该节点对应的两条边的序号,在vec
- 如果存在入度为2的节点:对应情况1和情况2
- 而情况1和2的区别在于,逆序删除边后,剩下的节点和边组成的是否还是组成树,而不是环,那么就用到了并查集
- 使用并查集判断删除vec[0]后的节点是否成环,不成环为情况1,可以删除当前序号对应的边
- 否则为情况2,删除vec[1]对应的边
- 不存在入度为2的节点,存在环,直接使用并查集查找使之成环的边,并删除(即打印)。
PS:使用并查集查找是否成环用的是上一题
学习收获:
冗余连接:无向图,直接用并查集找到使之成环的边即可
冗余连接Ⅱ:三种情况,需要统计入度,区分删除一个节点后是否成环,以及原节点和边组成的有向图是否成环