题目传送门（洛谷）
题目传送门（atcode）

Step 0 笑点解析

本题题目中的 log 提醒我们使用 $O(nlogn)$ 的算法（实际意思为木头）

Step 1 题意解释

• 输入一个数 $n$ 和 一个数 $k$，并给你一个长度为 $n$ 的序列 $a_1,a_2,...,a_n$.。
• 你要进行 $k$ 次操作，每次操作可以将 $a_i$ 分成两部分 $t$ 和 $a_i-t$
• 问在 $k$ 次操作后，最大的数最小是多少
• $1\le N\le 2\times 10^5$ $0\le K\le 10^9$ $1\le a_i\le 10^9$

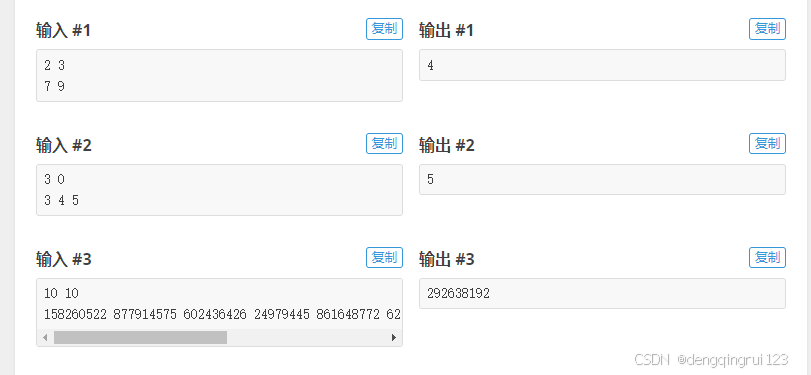
Step 2 样例解释

• 首先，我们在长度为 7 的木头上距离端点为 3.5 处切割，得到两根长度都是 3.5的木头。
• 接着，我们在长度为 9 的木头上距离端点为 3 处切割，得到长度分别为 3 和 6 的两根木头。
• 最后，我们在长度为 6 的木头上距离端点为 3.3处切割，得到长度分别为 3.5 和 2.5的两根木头。
• 在这种情况下，木头的最长长度将是 3.5。取上整后输出结果应为 4。

Step 3 解法分析

1. 考虑到题目中出现的特殊语句—— 最大的值最小 和 $1\le a_i\le 10^9$ 的数据范围，于是使用时间复杂度为 $O(nloga)$ 的二分答案。
2. 于是考虑二分答案，也就是二分可以的最长长度 $ans$，计算出让所有长度小于 $ans$ 所需要刀数，并判断是否合法，再二分，直到找到答案为止。
3. 如何 check 我们要将一个数 $x$ 切成不大于 $ans$的段，那么每次切的长度最大可以为
   $\lceil \frac{x}{ans}\rceil -1$ 段，我们要判断是否合法，只需要计算 ${\sum }_{i=1}^n\lceil \frac{x}{ans}\rceil -1$ 是否大于等于 $k$ 即可。

Step 4 Ac code

#include<bits/stdc++.h>
#define ll long long

using namespace std;

int n,k; 
int a[1000005];

bool check(double hhh){//二分的过程
	int ans = 0;
	for(int i = 1; i <= n ;i++){
		ans += ((a[i] - 1) / hhh);//判断每棵树最多可以切成几段
	}
	if(ans > k) return 0;
	return 1;
}

int main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin >> n >> k;
	for (int i = 1; i <= n ;i++)	cin >> a[i];
	double l = 1e-5,r = 1e9;
	while(r - l > 0.00001){//注意本题由于可以切出小数所以要用0.00001
		double mid = (l + r) / 2;
		//cout << l << " "<<mid<< " "<< r << "\n";
		if(check(mid)) r = mid;
		else l = mid;
	} 
	cout <<(int) (r + 1 - 1e-6)<<"\n";
	return 0;
}

谢谢各位的观看！！