1.原理
1.1 博弈关系
1.1.1 对抗训练
GAN的生成原理依赖于生成器和判别器的博弈
- 生成器试图生成以假乱真的样本。
- 判别器试图区分真假样本。
这种独特的机制使GAN在图像生成、文本生成等领域表现出色。
具有表现为:
-
生成器 (Generator, G)
生成器的目标是从一个随机噪声(通常是服从某种分布的向量,例如高斯分布或均匀分布)中生成与真实数据分布尽可能相似的样本。 -
判别器 (Discriminator, D)
判别器的目标是区分真实数据(来自真实数据分布)和生成器生成的数据,以分类器的形式输出一个概率值。
1.1.2 非零和博弈
零和博弈的参与者只能通过掠夺系统内部资源创造收益,类似压榨和内卷)。因为系统没有增量,也叫存量博弈。
但GAN的训练造成难以训练的生成器G,得到有效的训练,即数据生成能力(扩维任务)。
而D的分类任务相对于生成任务,较为简单(降维任务),虽然训练的表面结果是D的分类准确性下降(即G以假乱真)。
但并不能说明D的分类能力下降,因为分类的难度随着G的生成性能提升,其难度也是逐渐上升的。
可以理解为D是一个辅助训练的模型,其不是训练的目的。
1.2 推理方法
-
显式推理(Explicit Inference):对目标分布 p d a t a ( x ) p_{data}(x) pdata(x)进行明确建模或假设。
-
隐式推断(Implicit Inference): 不直接建模目标分布的显式形式(不计算概率),以间接方式生成符合目标分布的样本。
GAN是隐式推断,即构造一种生成过程间接逼近真实样本分布。
1.3 目标函数
生成器的目标:使生成的样本能够骗过判别器,即最大化:
log ( D ( G ( z ) ) ) \log(D(G(z))) log(D(G(z)))
判别器的目标:准确地辨别真实数据和伪造数据,即最大化
log ( D ( x ) ) + l o g ( 1 − D ( G ( z ) ) ) \log(D(x)) + log(1-D(G(z))) log(D(x))+log(1−D(G(z)))
这两部分的损失函数可以综合为一个对抗损失函数:
min G max D V ( D , G ) = E x ∼ p data ( x ) [ log D ( x ) ] + E z ∼ p z ( z ) [ log ( 1 − D ( G ( z ) ) ) ] \min\limits_G \max\limits_D V(D, G) = \mathbb{E}_{x \sim p_{\text{data}}(x)}[\log D(x)] + \mathbb{E}_{z \sim p_z(z)}[\log(1 - D(G(z)))] GminDmaxV(D,G)=Ex∼pdata(x)[logD(x)]+Ez∼pz(z)[log(1−D(G(z)))]
理论上,当GAN训练收敛时,生成器生成的数据分布与真实数据分布完全相同,此时判别器无法区分真实数据和生成数据,输出的概率接近 0.5。
2. 训练
2.1 训练策略
设计GAN生成Fashion-MNIST
-
G不断改进生成样本的质量,
-
D判别器不断提升辨别能力
-
D和G通过交替训练:
-
更新 D 时,不依赖 G 的计算图: 判别器只用生成器生成的假数据作为静态输入,不涉及生成器参数或计算图。
-
更新 G 时,依赖 D 的计算图: 判别器的计算图用于传递梯度信号,指导生成器优化。
-
pytorch中用detach()截断生成器的计算图:
fake_data = generator(z).detach()
G收敛时停止
2.2 代码
- 导入必要库
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
from torch.utils.data import DataLoader
- 定义生成器和判别器网络:
- 生成器G将随机噪声 z 转化为数据分布,通过Tanh调整到[-1,1]。
- 判别器D将输入(真实或生成)分类为真实或虚假, 通过Sigmooid输出为概率值[0,1]。
G和D都是三层全连接网络
class Generator(nn.Module):
def __init__(self, noise_dim):
super(Generator, self).__init__()
self.model = nn.Sequential(
nn.Linear(noise_dim, 256),
nn.ReLU(),
nn.Linear(256, 512),
nn.ReLU(),
nn.Linear(512, 1024),
nn.ReLU(),
nn.Linear(1024, 28*28),
nn.Tanh() # 输出范围 [-1, 1]
)
def forward(self, z):
img = self.model(z)
return img.view(-1, 1, 28, 28) # 调整为 1x28x28
class Discriminator(nn.Module):
def __init__(self):
super(Discriminator, self).__init__()
self.model = nn.Sequential(
nn.Linear(28*28, 1024),
nn.LeakyReLU(0.2),
nn.Dropout(0.3),
nn.Linear(1024, 512),
nn.LeakyReLU(0.2),
nn.Dropout(0.3),
nn.Linear(512, 256),
nn.LeakyReLU(0.2),
nn.Linear(256, 1),
nn.Sigmoid() # 输出概率值
)
def forward(self, img):
img_flat = img.view(img.size(0), -1) # 展平
return self.model(img_flat)
- 定义超参数和数据加载器
# 数据预处理
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,)) # 将像素值归一化到 [-1, 1]
])
# 加载数据集
train_dataset = torchvision.datasets.FashionMNIST(root='./data', train=True, download=True, transform=transform)
# 超参数
noise_dim = 100
lr = 0.0002
num_epochs = 50
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
- 初始化模型和优化器
# 初始化生成器和判别器
generator = Generator(noise_dim).to(device)
discriminator = Discriminator().to(device)
# 优化器
optimizer_G = optim.Adam(generator.parameters(), lr=lr, betas=(0.5, 0.999))
optimizer_D = optim.Adam(discriminator.parameters(), lr=lr, betas=(0.5, 0.999))
# 损失函数
criterion = nn.BCELoss() # 二元交叉熵损失
- 训练过程
for epoch in range(num_epochs):
for i, (real_imgs, _) in enumerate(train_loader):
batch_size = real_imgs.size(0)
# 真实标签和假标签
real_labels = torch.ones(batch_size, 1).to(device)
fake_labels = torch.zeros(batch_size, 1).to(device)
# ---------------------
# 训练判别器
# ---------------------
real_imgs = real_imgs.to(device)
z = torch.randn(batch_size, noise_dim).to(device)
fake_imgs = generator(z).detach() # 假图像,不更新生成器
real_loss = criterion(discriminator(real_imgs), real_labels)
fake_loss = criterion(discriminator(fake_imgs), fake_labels)
d_loss = real_loss + fake_loss
optimizer_D.zero_grad()
d_loss.backward()
optimizer_D.step()
# ---------------------
# 训练生成器
# ---------------------
z = torch.randn(batch_size, noise_dim).to(device)
fake_imgs = generator(z)
g_loss = criterion(discriminator(fake_imgs), real_labels) # 目标是骗过判别器
optimizer_G.zero_grad()
g_loss.backward()
optimizer_G.step()
# 打印损失
print(f"Epoch [{epoch+1}/{num_epochs}] | D Loss: {d_loss.item():.4f} | G Loss: {g_loss.item():.4f}")
# 每个 epoch 保存一些生成图像
if (epoch + 1) % 10 == 0:
with torch.no_grad():
z = torch.randn(16, noise_dim).to(device)
samples = generator(z).cpu().numpy()
samples = (samples + 1) / 2 # 转换回 [0, 1] 范围
fig, axs = plt.subplots(4, 4, figsize=(5, 5))
for ax, img in zip(axs.flatten(), samples):
ax.imshow(img.squeeze(), cmap='gray')
ax.axis('off')
plt.show()
- 生成新样本
import matplotlib.pyplot as plt
z = torch.randn(16, latent_dim).to('cuda')
generated_images = generator(z).view(-1, 1, 28, 28).cpu().detach()
grid = torchvision.utils.make_grid(generated_images, nrow=4, normalize=True)
plt.imshow(grid.permute(1, 2, 0))
plt.show()
3. 实验
3.1 参数设置
- 数据集:Fashion-Mnist
- batch_size =128
- 损失函数 = BCE
- Learning_rate = 2e-4
- epoch = 50
3.2 模型结构
- D和G同样是三层fc结构 (GPU显存消耗 = 约 287mb)
- D=3层fc,G=4层conv (GPU显存消耗 = 约 603mb)
- D和G都是4层conv (GPU显存消耗 = 约 811mb)
3.3 实验结果
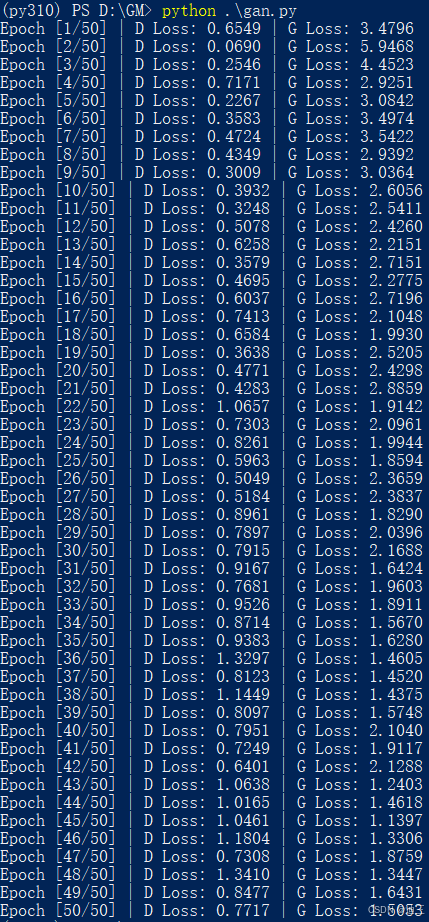
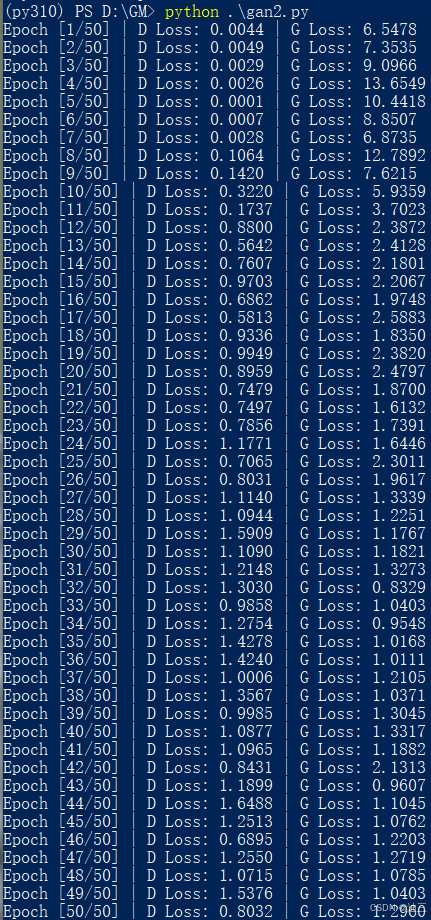
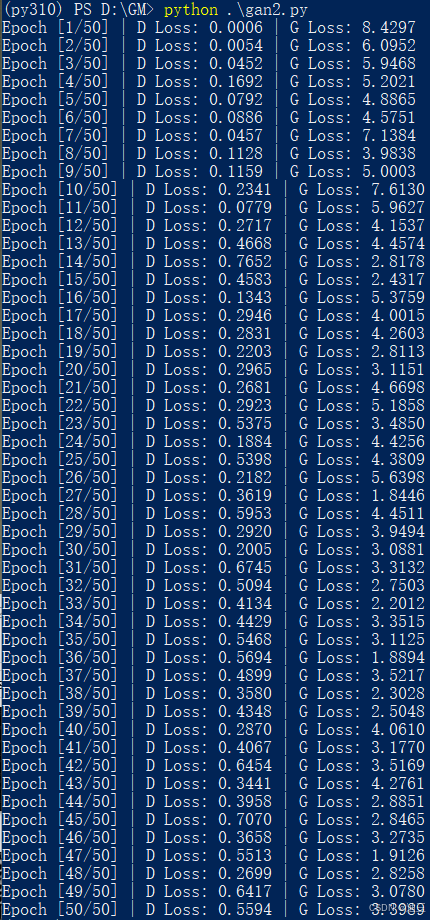
从左到右分别是上述三种结构的结果,其他参数不变
3.3.1 损失变化
双conv的
-
前两种结构D的损失偏大,即分类错误率较高,G的损失有所收敛
-
双conv的判别器损失在0.5左右,即真假难辨,G的损失没有收敛
3.3.2 定性比较
- 3 epoch



3次数据集迭代后的表现,只有FC结构有快速收敛的趋势,和模型参数较小有关。
- 48 epoch
结论:3层FC的G和D效果(性能)较差,4层conv的G和D效果最好, 适当增加模型的参数规模, 用CONV替换FC能取得更佳性能
4. 其他改进
GAN原有的交叉熵损失(BCE)是训练不稳定的原因之一, 因此有很多改进方法,这里介绍2种常见的改进方法:
4.1 BCE
BCE 是经典的二分类任务损失函数,衡量预测概率与真实标签之间的差距。,该公式本质上是最大化预测概率与真实标签一致的对数似然(log-likelihood),即最大似然估计(Maximum Likelihood Estimation, MLE)。
判别器的输出是一个概率值 D(x)∈[0,1],表示输入样本 x 属于真实样本的概率。
生成器的目标是让D(G(z)) 接近 1,从而欺骗判别器。、
由于似然函数是多个概率的乘积,直接计算可能会得到很小的值产生下溢。通过对似然函数取对数,将乘积转化为求和,更容易计算和优化:
$\text{BCE}(y, \hat{y}) = -\frac{1}{N} \sum_{i=1}^N \left[ y_i \log(\hat{y}_i) + (1 - y_i) \log(1 - \hat{y}_i) \right]
$
4.2 对数函数缺点
该损失会造成生成器训练不稳定
生成器根据损失函数如下:
$\mathcal{L}G = -\mathbb{E}{z \sim p_z} \left[\log D(G(z))\right]
$
求导更新梯度:
∇ θ G L G = − E z ∼ p z [ 1 D ( G ( z ) ) ⋅ ∇ θ G D ( G ( z ) ) ] \nabla_{\theta_G} \mathcal{L}_G = -\mathbb{E}_{z \sim p_z} \left[\frac{1}{D(G(z))} \cdot \nabla_{\theta_G} D(G(z))\right] ∇θGLG=−Ez∼pz[D(G(z))1⋅∇θGD(G(z))]
梯度 ∇ \nabla ∇是更新的方向为负值(即方向为降低D的值)
-
当D的输出接近0,当图像判别为假, 1 / D ( ) 1/D() 1/D() 过大,梯度值过大。
-
当D的输出接近1,当图像判别为真, 1 / D ( ) 1/D() 1/D() 为1,梯度值为 ∇ \nabla ∇过小。
为此,改进的方式就是去掉对数函数log
4.2 LSGAN
LSGAN 损失函数的目标是最小化生成器和判别器之间的预测值和目标值之间的平方误差, MSE可以理解为其均值形式。
- D Loss
L D = 1 2 E x ∼ p data [ ( D ( x ) − 1 ) 2 ] + 1 2 E z ∼ p z [ D ( G ( z ) ) 2 ] \mathcal{L}_D = \frac{1}{2} \mathbb{E}_{x \sim p_{\text{data}}} \left[ (D(x) - 1)^2 \right] + \frac{1}{2} \mathbb{E}_{z \sim p_z} \left[ D(G(z))^2 \right] LD=21Ex∼pdata[(D(x)−1)2]+21Ez∼pz[D(G(z))2]
- G Loss
L G = 1 2 E z ∼ p z [ ( D ( G ( z ) ) − 1 ) 2 ] \mathcal{L}_G = \frac{1}{2} \mathbb{E}_{z \sim p_z} \left[ (D(G(z)) - 1)^2 \right] LG=21Ez∼pz[(D(G(z))−1)2]
由于非概率输出,这里的D可以移除最后的sigmoid激活函数。
4.4 WGAN
WGAN 使用 Wasserstein 距离,(也叫 Earth-Mover Distance) 作为目标函数来训练模型
JS 散度(Jensen-Shannon Divergence)
- G Loss
L G = − E z ∼ p z [ D ( G ( z ) ) ] \mathcal{L}_G = - \mathbb{E}_{z \sim p_z} \left[ D(G(z)) \right] LG=−Ez∼pz[D(G(z))]
- D Loss
L D = E x ∼ p data [ D ( x ) ] − E z ∼ p z [ D ( G ( z ) ) ] \mathcal{L}_D = \mathbb{E}_{x \sim p_{\text{data}}} \left[ D(x) \right] - \mathbb{E}_{z \sim p_z} \left[ D(G(z)) \right] LD=Ex∼pdata[D(x)]−Ez∼pz[D(G(z))]
和LSGAN类似,D需要移除sigmoid, 即输出不需要限制在[0,1]范围内,直接输出实值
另外,WGAN损失的是通过 Kantorovich-Rubinstein 对偶函数定义,成立条件是梯度变化满足1-Lipschitz连续性,
即每次更新D梯度不能太大,需要对D的权重进行剪切(clipping):,
for param in D.parameters():
param.data.clamp_(-c, c) #这里裁剪范围是[-c,c],具体根据实验经验设置
4.5 WGAN-GP
WGAN的梯度裁剪不够优雅,表现在裁剪的c值是间接约束梯度,无法控制梯度的实际值,导致:
-
c容易设置过小,导致不满足1-Lipschitz连续性连续性,训练失败
-
c容易设置过大,过度裁剪会降低判别器的学习能力,导致训练收敛速度过慢,甚至效果不佳。
WGAN-GP通过构造一个真假图像( x x x与 x ^ \hat{x} x^)的插值样本 x ~ \tilde{x} x~, 确保插值样本均匀分布在真实样本和生成样本的连接区域上。即插值样本提供了一个中间空间,涵盖了真实分布和生成分布的边界区域,通常是判别器最难判别的部分,即D的梯度变化最激烈的部分。
为保证该区域满足 1-Lipschitz 条件,直接计算样本输入D的梯度,并正则化项约束这个梯度作为梯度约束项(gradient_penalty),惩罚其与目标值 1 的偏差,以保证梯度的2范数接近 1:
KaTeX parse error: Got function '\hat' with no arguments as subscript at position 44: …\hat{x} \sim p_\̲h̲a̲t̲{x}} \left[ D(\…
其中插值图像:
x ~ = α x − ( 1 − α ) x ^ ; α ∼ U n i f o r m ( 0 , 1 ) \tilde{x} = \alpha x - (1- \alpha)\hat{x}; \hspace{1em} \alpha \sim \mathcal{Uniform}(0,1) x~=αx−(1−α)x^;α∼Uniform(0,1)
梯度惩罚项:
[ ( ∥ ∇ x ~ D ( x ~ ) ∥ 2 − 1 ) 2 ] \left[ \left( \|\nabla_{\tilde{x}} D(\tilde{x})\|_2 - 1 \right)^2 \right] [(∥∇x~D(x~)∥2−1)2]
梯度惩罚的权重超参数 λ \lambda λ默认为10
gradient_penalty 的 pytrch代码如下:
def gradient_penalty(critic, real_samples, fake_samples):
alpha = torch.rand(real_samples.size(0), 1, device=device)
alpha = alpha.expand_as(real_samples)
interpolates = (alpha * real_samples + (1 - alpha) * fake_samples).requires_grad_(True)
critic_output = D(interpolates)
gradients = torch.autograd.grad(
outputs=critic_output,
inputs=interpolates,
grad_outputs=torch.ones_like(critic_output, device=device),
create_graph=True,
retain_graph=True,
only_inputs=True
)[0]
gradients = gradients.view(gradients.size(0), -1)
gradient_norm = gradients.norm(2, dim=1)
penalty = ((gradient_norm - 1) ** 2).mean()
return penalty
Ref
本篇代码在:
- https://github.com/disanda/GM/blob/main/gan.py
fc结构的GAN
- https://github.com/disanda/GM/blob/main/gan2.py
conv结构的GAN, 也叫DCGAN
参考文献
- https://arxiv.org/abs/1406.2661
Generative Adversarial Networks, GAN, 2014, nips
- https://arxiv.org/abs/1611.04076
Least Squares Generative Adversarial Networks, LSGAN, 2016
- https://arxiv.org/abs/1701.07875
Wasserstein GAN, WGAN, 2017
- https://arxiv.org/abs/1704.00028
Improved Training of Wasserstein GANs, WGAN-GP, 2017
- https://arxiv.org/abs/1511.06434
DCGAN, 2016, ICLR


