引言
对于计算机科学来说,数据结构几乎是编程语言之后必学的科目,也是在编程世界中继续徜徉的必要工具。计算机是一台只认识0和1的毫不埋怨的听话机器,但使用计算机的人们却没那么好耐心,当我把数据交给计算机处理的时候,它必需快速、准确,又能易于人类理解的方式,毕竟人去给它编程,它自己还不能自己思考。所以,就由数据结构来组织这些数据,实现计算机工作的算法。
什么是数据结构
数据结构是数据对象,以及存在于该对象的实例和组成实例的数据元素之间的各种联系。这些联系可以通过定义相关的函数来给出。
这是大牛给出的定义,熟悉数据结构的人看到这么牛逼的定义还是会中肯地点点头,不过照我的理解,数据结构就是人类想象的计算机把数据组织起来的方式,计算机不会认识树,栈,队列,但是通过这种组织方式,再使用某种方式(也就是函数),实现快速的增加数据,查找数据,来让现代焦虑的人们享有一丝快感。毕竟,计算机没我们想象的那么聪明,它只会做无聊的重复的工作,一直做,哪怕人类毁灭,它也don’t care。
为什么要使用数据结构
因为快,准,使一些人类头痛的问题,比如给10^10个数排序,让计算机去优雅的解决,我们安心喝喝茶就好了,不过可能喝不了多少。
算法分析
数据结构中,常常同时出现的词就是算法,二者不必分开看待,抽象点的话,我觉得数据结构是“硬件“,而算法是“软件“;具象一点,数据结构就是“数组“,算法就是“for循环“。当然以上只是我粗鄙的理解。具体的解释请看这里——算法的维基定义。
由于算法和数据结构本质上是可以看做一体的,所以二者的分析也是通用的。有好的数据结构,就有差的数据结构,怎么去分析呢,我们一般从人类诞生时便产生的哲学问题入手——时间和空间。
时间复杂度
算法的时间在不运行的情况下,只需要去分析每行代码的执行次数就行了,为了便于分析,通常只记录循环执行的次数,嵌套的循环需要乘起来,并列的循环只要加起来就行了,为了更简便,使用大O记号来记录,只取多项式的最高阶作为其复杂度。例如一段代码的执行次数为
10n2+5n+7
次,使用大O记号,时间复杂度为O(
n2
)。
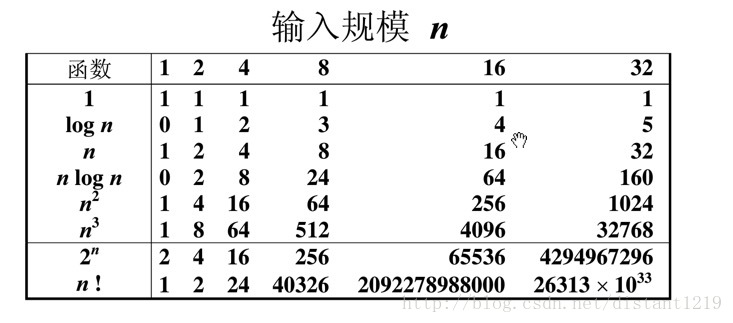
由以上表可见,在数据规模逐渐增大的时候,时间的增加是可怕的。只能,待人类造出更快的计算机了(^^)。
空间复杂度
随着存储技术的发展,存储的价格变得便宜了,所以在有些时候,以空间换取时间。但是秉着节约的好习惯,我们还是要尽量省。
空间复杂度为计算变量在内存所占的空间。这与语言和变量类型,例如在64位机上,C/C++的int类型占4个字节。这要根据具体情况分析。耗费空间的情况通常为:
- 开巨大巨大的数组;
- 递归太深,导致爆内存。
一般遇到存储不足的情况,可以分析一下这两种情况。
数据结构的种类
说到这里,数据结构类型许许多多,实现方法多样,但背后原理都是一样的。
常见的数据类型有:
- 线性表:数组(Array)和链表(Linked List)
- 栈(Stack)
- 队列(Queue)
- 散列表(Hash)
- 树(Tree)
- 图(Graph)
在一些高级语言中,都有已经写好的类库供程序员调用,但本着学习的态度,还是要自己实现一下,再学一下标准类库的源码,会有更大的收获。