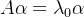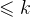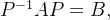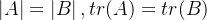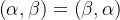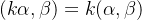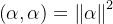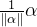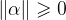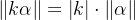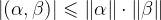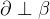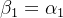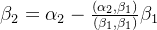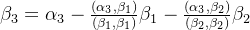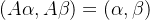5.1 矩阵的特征值与特征向量
5.1.1 矩阵的特征值与特征向量
定义:设A是n阶方阵,若对于数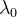
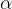
则称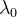
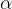
的特征向量
定义: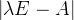

5.1.2 特征值与特征向量的基本性质
性质:
1)n阶矩阵A与其转置矩阵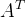
2)设n阶矩阵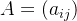
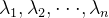
(1) 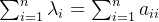
(2)
3)n阶矩阵A可逆的充要条件是A的所有特征值都不等于零
4)n阶矩阵A的互不相同的特征值

5)k重特征值对应的线性无关的特征向量个数
其他性质:
设
1)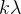
2)
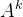
3)若
,则
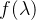
的特征值
4)若矩阵A可逆,则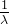
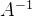

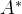
5.2 相似矩阵与矩阵可对角化的条件
5.2.1 相似矩阵的概念
定义:设A与B是n阶矩阵,若存在n阶矩阵P,使得
则称矩阵A与B相似,记为A~B
性质:
1)反身性:A~A
2)对称性:若A~B,则B~A
3)传递性:若A~B,B~C,则A~C
5.2.2 相似矩阵的性质
性质:
1)若A~B,则A与B有相同的特征值,从而
2)若A~B,则A可逆的充要条件是B可逆,而且当A,B都可逆时,有
3)若A~B,则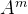
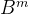
5.2.3 矩阵与对角形矩阵相似的条件
定理:n阶矩阵A相似于对角线矩阵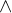
5.3 实对称矩阵的对角化
所有的实对称矩阵都能对角化
5.3.1 向量的内积与正交向量组
内积:
内积的性质:
1)非负性: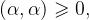
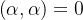
2)对称性:
3)齐次性:
4)线性性:
向量的长度(范数/模)
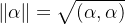
单位向量:长度为1的向量
单位化或标准化:
长度的性质:
1)非负性:
2)齐次性:
3)柯西——施瓦茨不等式:
4)三角不等式:
正交(垂直):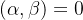
正交向量组:不含有零向量,向量两两正交
标准正交向量组:正交向量组中每一个向量都是单位向量
定理:

5.3.2 施密特正交化
给一组无关的
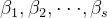
```````
第一步:施密特正交化
第二步:施密特单位化
5.3.3 正交矩阵
定义:设A为n阶矩阵,且
性质:
1)若A为正交矩阵,则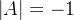
2)若A为正交矩阵,则
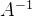
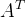
3)若A,B均为n阶正交矩阵,则AB也是正交矩阵
4)若A是n阶正交矩阵,
定理:n阶矩阵A为正交矩阵的充要条件是A的列(行)向量组是标准正交向量组
5.3.4 实对称矩阵的对角化
定理:n阶实对称矩阵A的n个特征值都是实数,且其特征向量是实向量
定理:实对称矩阵A的对应于不同特征值的特征向量必正交
定义:设A,B为同阶矩阵,若存在同阶正交矩阵P,使得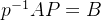
定理:设A为n阶实对称矩阵,则存在正交矩阵Q,使得