摘要
ReLU-KAN 结合了ReLU(Rectified Linear Unit,线性整流函数)和Kolmogorov-Arnold网络的特性,同时强调了其仅需要矩阵加法、点乘和ReLU这三种基本运算。
BottleNeckReLUKANConv2DLayer在ReLU-KAN上加入瓶颈结构。
基本概念
- ReLU-KAN:一种创新的神经网络架构,旨在通过简化计算过程来提高效率,同时保持或增强网络的学习能力。
- ReLU:一种常用的激活函数,用于解决梯度消失问题,并加速训练过程。它将输入的所有负值置为0,保持正值不变。
- Kolmogorov-Arnold表示定理(或类似概念):可能指的是一种用于表示复杂函数为一系列较简单函数组合的数学理论。在网络架构中,这可能意味着将复杂的映射任务分解为多个简单的层或操作。
核心特点
- 计算高效:通过仅使用矩阵加法、点乘和ReLU这三种基本运算,
ReLU-KAN大大简化了计算过程,提高了运算效率。 - 学习能力强:尽管操作简单,但结合ReLU的激活特性和Kolmogorov-Arnold表示定理的分解思想,
ReLU-KAN可能具有强大的学习能力,能够处理复杂的任务。 - 灵活性:由于基于基本的数学运算,
ReLU-KAN可能更容易与其他类型的网络或算法相结合,以适应不同的应用场景。
应用前景
ReLU-KAN可能适用于需要高效计算和强大学习能力的各种领域,如图像识别、自然语言处理、时间序列分析等。其简化的计算过程可能使得在资源受限的环境(如移动设备或嵌入式系统)中部署深度学习模型变得更加可行。
论文翻译:《ReLU-KAN:仅需要矩阵加法、点乘和ReLU_的新型Kolmogorov-Arnold网络》
https://arxiv.org/pdf/2406.02075
由于基函数(B样条)计算的复杂性,Kolmogorov-Arnold网络(KAN)在GPU上的并行计算能力受到限制。本文提出了一种新的ReLU-KAN实现方法,该方法继承了KAN的核心思想。通过采用ReLU(修正线性单元)和逐点乘法,我们简化了KAN基函数的设计,并优化了计算过程以实现高效的CUDA计算。所提出的ReLU-KAN架构可以轻松地部署在现有的深度学习框架(如PyTorch)中,用于推理和训练。实验结果表明,与具有4层网络的传统KAN相比,ReLU-KAN实现了20倍的速度提升。此外,ReLU-KAN在保持KAN的“灾难性遗忘避免”特性的同时,还展现出了更稳定的训练过程和更优的拟合能力。您可以在https://github.com/quiqi/relu_kan获取代码。
关键词:Kolmogorov-Arnold网络 - 并行计算 - 修正线性单元
1、引言
Kolmogorov-Arnold网络(KANs)[1]因其出色的性能和新颖的结构[2,3]而最近备受关注。研究人员迅速采用KANs来解决各种问题[4,5]。然而,阻碍其更广泛应用的一个关键挑战是无法充分利用GPU的并行处理能力。这一瓶颈源于KANs样条函数设计的固有复杂性,最终影响了处理速度和可扩展性。
本文介绍了一个简化的基函数:
R i ( x ) = [ ReLU ( e i − x ) × ReLU ( x − s i ) ] 2 × 16 / ( b i − a i ) 4 R_{i}(x)=\left[\text{ReLU}\left(e_{i}-x\right) \times \text{ReLU}\left(x-s_{i}\right)\right]^{2} \times 16 /\left(b_{i}-a_{i}\right)^{4} Ri(x)=[ReLU(ei−x)×ReLU(x−si)]2×16/(bi−ai)4
其中, ReLU ( x ) = max ( 0 , x ) \text{ReLU}(\text{x})=\max (0, x) ReLU(x)=max(0,x)[6],并基于这个简化的基函数优化了KAN操作,以实现高效的GPU并行计算。首先,我们将整个基函数的计算表示为矩阵运算,以充分利用GPU的并行处理能力。其次,类似于Transformer中的位置编码[7],我们预先生成非训练参数以加速计算。最后,我们将基函数的加权和表示为卷积运算,这使得新的KAN架构能够轻松地在现有的深度学习框架上实现。我们使用PyTorch实现了KAN架构的核心代码,代码行数不到30行。在本文中,这种新的KAN架构被称为ReLU-KAN。
我们在原始KAN论文中使用的一组函数上对ReLU-KAN的性能进行了评估。与KAN相比,ReLU-KAN在训练速度、收敛稳定性和拟合精度方面表现出了显著的改进,特别是在较大的网络架构中。值得注意的是,ReLU-KAN继承了KAN的大多数关键属性,包括网格数量等超参数以及防止灾难性遗忘的能力。
具体而言,在现有实验中,ReLU-KAN的训练速度是KAN的5到20倍,且ReLU-KAN的准确度比KAN高出2个数量级。
本文的主要贡献如下:
- 简化的基函数:我们引入了一个简化的基函数 R ( x ) \mathrm{R}(\mathrm{x}) R(x),它在保持原始KAN基函数拟合能力的同时,提高了计算效率。
- 基于矩阵的KAN操作:在简化基函数的基础上,我们优化了KAN操作,以实现高效的矩阵计算。这种优化使得与GPU处理的兼容性更好,并便于在现有的深度学习框架中实现。
在后续章节中,我们将详细介绍我们的贡献:在第2节中,我们将介绍KAN,并将其概念化为多层感知器(MLPs)的扩展。我们将提供KAN的高级概述,并探讨构建类似网络架构的潜在方法;在第3节中,我们将介绍ReLU-KAN架构,重点介绍其核心组件和高效的PyTorch实现;在第4节中,我们将进行全面的实验,以评估ReLU-KAN与KAN的性能。我们将探讨ReLU-KAN在训练速度、收敛稳定性和拟合精度方面的优势,特别是对于较大的网络。此外,我们还将验证ReLU-KAN防止灾难性遗忘的能力。
2、相关工作
本节概述了Kolmogorov-Arnold网络(KANs)。由于我们的工作主要集中在改进KAN的基函数上,因此我们将更深入地探讨B样条函数在KAN架构中的作用。
2.1、将Kolmogorov-Arnold网络作为MLP的扩展
Kolmogorov-Arnold表示定理确认了一个高维函数可以表示为有限数量的一维函数的组合,如等式2所示。
f ( x ) = ∑ i = 1 2 n + 1 Φ i ( ∑ j = 1 n ϕ i , j ( x j ) ) f(x)=\sum_{i=1}^{2 n+1} \Phi_{i}\left(\sum_{j=1}^{n} \phi_{i, j}\left(x_{j}\right)\right) f(x)=∑i=12n+1Φi(∑j=1nϕi,j(xj))
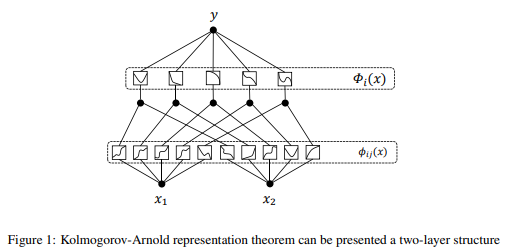
其中, ϕ i , j \phi_{i, j} ϕi,j被称为内函数, Φ i \Phi_{i} Φi被称为外函数。基于该定理的数学框架,Kolmogorov-Arnold表示定理可以表示为一个两层结构,如图1所示。我们考虑一个KAN,其中输入向量 x x x的长度为 n n n,输出为 y y y。等式3描述了图1。
y = ( Φ ( ⋅ ) 1 Φ ( ⋅ ) 2 ⋮ Φ ( ⋅ ) 2 n + 1 ) ( ( ϕ ( ⋅ ) 1 , 1 ϕ ( ⋅ ) 1 , 2 ⋯ ϕ ( ⋅ ) 1 , n ϕ ( ⋅ ) 2 , 1 ϕ ( ⋅ ) 2 , 2 ⋯ ϕ ( ⋅ ) 2 , n ⋮ ⋮ ⋱ ⋮ ϕ ( ⋅ ) n , 1 ϕ ( ⋅ ) n , 2 ⋯ ϕ ( ⋅ ) n , n ) x ) y=\left(\begin{array}{c} \boldsymbol{\Phi}(\cdot)_{1} \\ \boldsymbol{\Phi}(\cdot)_{2} \\ \vdots \\ \boldsymbol{\Phi}(\cdot)_{2 n+1} \end{array}\right)\left(\left(\begin{array}{cccc} \phi(\cdot)_{1,1} & \phi(\cdot)_{1,2} & \cdots & \phi(\cdot)_{1,n} \\ \phi(\cdot)_{2,1} & \phi(\cdot)_{2,2} & \cdots & \phi(\cdot)_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ \phi(\cdot)_{n, 1} & \phi(\cdot)_{n, 2} & \cdots & \phi(\cdot)_{n,n} \end{array}\right) \boldsymbol{x}\right) y= Φ(⋅)1Φ(⋅)2⋮Φ(⋅)2n+1 ϕ(⋅)1,1ϕ(⋅)2,1⋮ϕ(⋅)n,1ϕ(⋅)1,2ϕ(⋅)2,2⋮ϕ(⋅)n,2⋯⋯⋱⋯ϕ(⋅)1,nϕ(⋅)2,n⋮ϕ(⋅)n,n x
(注意:原式中的 ϕ ( ⋅ ) 1 , 2 n + 1 \phi(\cdot)_{1,2 n+1} ϕ(⋅)1,2n+1到 ϕ ( ⋅ ) n , 2 n + 1 \phi(\cdot)_{n,2 n+1} ϕ(⋅)n,2n+1应为笔误,已根据上下文更正为 ϕ ( ⋅ ) n , n \phi(\cdot)_{n,n} ϕ(⋅)n,n)
为了确保 ϕ i j \phi_{i j} ϕij和 Φ i \Phi_{i} Φi的表示能力,它们被表示为多个B样条函数和一个偏置函数的线性组合,如等式4所示:
ϕ ( x ) = w b x / ( 1 + e − x ) + w s ∑ c i B i ( x ) \phi(x)=w_{b} x /(1+e^{-x})+w_{s} \sum c_{i} B_{i}(x) ϕ(x)=wbx/(1+e−x)+ws∑ciBi(x)
其中,
B
i
(
x
)
B_{i}(x)
Bi(x)是一个B样条函数。
假设我们定义
ϕ
i
j
(
x
j
)
=
w
i
j
x
j
\phi_{i j}\left(x_{j}\right)=w_{i j} x_{j}
ϕij(xj)=wijxj,
Φ
i
(
x
)
=
ReLU
(
x
)
\Phi_{i}(x)=\operatorname{ReLU}(x)
Φi(x)=ReLU(x),则方程3可以视为一个多层感知机(MLP)。这个MLP接受一个n维输入,将其降维至一维输出,并采用了包含
2
n
+
1
2n+1
2n+1个节点的单个隐藏层。从这个意义上讲,KAN可以看作是MLP的一种扩展。激活函数在MLP中起着至关重要的作用,因为
ϕ
i
j
(
x
j
)
=
w
i
j
x
j
\phi_{i j}\left(x_{j}\right)=w_{i j} x_{j}
ϕij(xj)=wijxj缺乏非线性拟合能力。但如果
ϕ
i
j
(
x
)
\phi_{i j}(x)
ϕij(x)是一个非线性函数,则可以省略激活函数。
我们可以类似多层感知机(MLP)那样扩展KAN网络的隐藏层架构。因此,在放宽节点数必须为 2 n + 1 2n+1 2n+1的约束并忽略激活函数 Φ ( ⋅ ) \Phi(\cdot) Φ(⋅)后,处理n个输入并生成m个输出的隐藏层可以用方程5表示。KAN可以表示为方程5:
KAN hidden ( x ) = ( ϕ ( ⋅ ) 11 ϕ ( ⋅ ) 12 ⋯ ϕ ( ⋅ ) 1 n ϕ ( ⋅ ) 21 ϕ ( ⋅ ) 22 ⋯ ϕ ( ⋅ ) 2 n ⋮ ⋮ ⋱ ⋮ ϕ ( ⋅ ) m 1 ϕ ( ⋅ ) m 2 ⋯ ϕ ( ⋅ ) m n ) x \operatorname{KAN}_{\text {hidden }}(x)=\left(\begin{array}{cccc} \phi(\cdot)_{11} & \phi(\cdot)_{12} & \cdots & \phi(\cdot)_{1 n} \\ \phi(\cdot)_{21} & \phi(\cdot)_{22} & \cdots & \phi(\cdot)_{2 n} \\ \vdots & \vdots & \ddots & \vdots \\ \phi(\cdot)_{m 1} & \phi(\cdot)_{m 2} & \cdots & \phi(\cdot)_{m n} \end{array}\right) \boldsymbol{x} KANhidden (x)= ϕ(⋅)11ϕ(⋅)21⋮ϕ(⋅)m1ϕ(⋅)12ϕ(⋅)22⋮ϕ(⋅)m2⋯⋯⋱⋯ϕ(⋅)1nϕ(⋅)2n⋮ϕ(⋅)mn x
我们只需找到适合的非线性 ϕ ( x ) \phi(x) ϕ(x),就可以基于方程5构建更多类似KAN的结构。
2.2、B样条
在KAN中,一组B样条函数表示为
B
=
{
B
1
(
a
1
,
k
,
s
,
x
)
,
B
2
(
a
2
,
k
,
s
,
x
)
,
…
,
B
n
(
a
n
,
k
,
s
,
x
)
}
\boldsymbol{B}=\left\{B_{1}\left(a_{1}, k, s, x\right), B_{2}\left(a_{2}, k, s, x\right), \ldots, B_{n}\left(a_{n}, k, s, x\right)\right\}
B={B1(a1,k,s,x),B2(a2,k,s,x),…,Bn(an,k,s,x)},用作基函数来表示有限域上的任何一元函数。这些B样条函数形状相同但位置不同。每个项
B
i
(
a
i
,
k
,
s
,
x
)
B_{i}\left(a_{i}, k, s, x\right)
Bi(ai,k,s,x)都是一个钟形函数,其中
a
i
a_{i}
ai、
k
k
k和
s
s
s是
B
i
B_{i}
Bi的超参数。
a
i
a_{i}
ai用于控制对称轴的位置,
k
k
k决定非零区域的范围,而
s
s
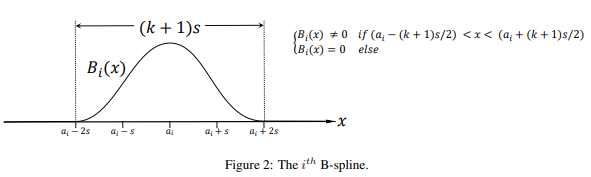
s是单位区间。图2展示了第
i
i
i个样条
B
i
B_{i}
Bi(假设
k
=
3
k=3
k=3)的图形。
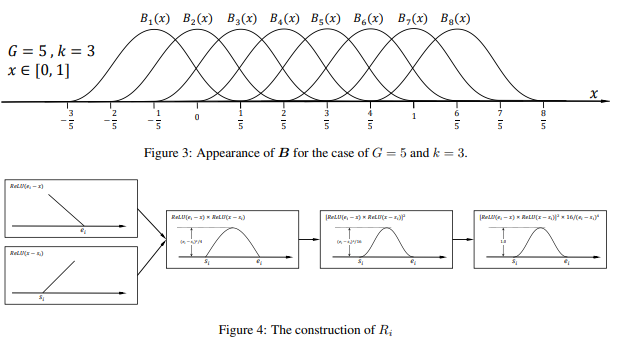
基函数集 B \boldsymbol{B} B的超参数取决于网格的数量,用 G G G表示。具体来说,当要近似的函数的域为 x ∈ [ 0 , 1 ] x \in[0,1] x∈[0,1]时,我们有 n = G + k n=G+k n=G+k个基函数,步长为 s = 1 / G s=1 / G s=1/G,且 a i = 2 i + 1 − k 2 G a_{i}=\frac{2 i+1-k}{2 G} ai=2G2i+1−k。图3展示了在 G = 5 G=5 G=5和 k = 3 k=3 k=3的情况下 B \boldsymbol{B} B的外观。
在KAN中,待拟合的函数
f
(
x
)
f(x)
f(x)表示为方程4。通过使用优化算法(如梯度下降法)来确定
w
b
w_{b}
wb、
w
s
w_{s}
ws和
c
=
[
c
1
,
c
2
,
…
,
c
n
]
\boldsymbol{c}=\left[c_{1}, c_{2}, \ldots, c_{n}\right]
c=[c1,c2,…,cn]的值,我们得到使用B样条函数拟合的
ϕ
(
x
)
\phi(x)
ϕ(x)。
增加网格数量 G G G会导致可训练参数的数量增加,从而增强模型的拟合能力。然而,较大的 k k k值会加强B样条函数之间的耦合,这同样可以提高拟合能力。由于 G G G和 k k k都是控制模型拟合能力的有效超参数,我们在ReLU-KAN架构中保留了它们。
样条函数 B i ( x ) B_{i}(x) Bi(x)是一个非常复杂的分段函数,因此样条函数的求解过程不能表示为矩阵运算,因此无法充分利用GPU的并行能力。
3、方法
3.1、ReLU-KAN
我们使用更简单的函数 R i ( x ) R_{i}(x) Ri(x) 来替换KAN中的B样条函数,作为新的基函数:
R i ( x ) = [ ReLU ( e i − x ) × ReLU ( x − s i ) ] 2 × 16 ( e i − s i ) 4 R_{i}(x)=\left[\text{ReLU}\left(e_{i}-x\right) \times \text{ReLU}\left(x-s_{i}\right)\right]^{2} \times \frac{16}{\left(e_{i}-s_{i}\right)^{4}} Ri(x)=[ReLU(ei−x)×ReLU(x−si)]2×(ei−si)416
其中,
ReLU
(
x
)
=
max
(
0
,
x
)
\text{ReLU}(x)=\max (0, x)
ReLU(x)=max(0,x)。
很容易发现,当
x
=
(
e
i
+
s
i
)
/
2
x=\left(e_{i}+s_{i}\right) / 2
x=(ei+si)/2 时,
ReLU
(
e
i
−
x
)
×
ReLU
(
x
−
s
i
)
\text{ReLU}\left(e_{i}-x\right) \times \text{ReLU}\left(x-s_{i}\right)
ReLU(ei−x)×ReLU(x−si) 的最大值为
(
e
i
−
s
i
)
2
4
\frac{\left(e_{i}-s_{i}\right)^{2}}{4}
4(ei−si)2,所以
[
ReLU
(
e
i
−
x
)
×
ReLU
(
x
−
s
i
)
]
2
\left[\text{ReLU}\left(e_{i}-x\right) \times \text{ReLU}\left(x-s_{i}\right)\right]^{2}
[ReLU(ei−x)×ReLU(x−si)]2 的最大值为
(
e
i
−
s
i
)
4
16
\frac{\left(e_{i}-s_{i}\right)^{4}}{16}
16(ei−si)4,而
16
(
e
i
−
s
i
)
4
\frac{16}{\left(e_{i}-s_{i}\right)^{4}}
(ei−si)416 用作归一化常数。
和
B
i
(
x
)
B_{i}(x)
Bi(x) 一样,
R
i
(
x
)
R_{i}(x)
Ri(x) 也是一个单变量钟形函数,它在
x
∈
[
s
i
,
e
i
]
x \in\left[s_{i}, e_{i}\right]
x∈[si,ei] 时非零,在其他区间为零。使用
ReLU
(
x
)
\text{ReLU}(x)
ReLU(x) 函数来限制非零值的范围,并使用平方操作来增加函数的平滑性。如图4所示。
多个基函数
R
i
R_{i}
Ri 可以形成基函数集
R
=
{
R
1
(
x
)
,
R
2
(
x
)
,
…
,
R
n
(
x
)
}
\boldsymbol{R}=\left\{R_{1}(x), R_{2}(x), \ldots, R_{n}(x)\right\}
R={R1(x),R2(x),…,Rn(x)},
R
\boldsymbol{R}
R 继承了
B
\boldsymbol{B}
B 的许多属性。它再次由
n
n
n 个形状相同但位置不同的基函数组成,并且基函数的数量
n
n
n 以及
a
i
,
b
i
a_{i}, b_{i}
ai,bi 也由网格的数量
G
G
G 和跨度参数
k
k
k 决定。
通过多个基函数
R
i
R_{i}
Ri 可以构造出一组基函数集,记作
R
=
{
R
1
(
x
)
,
R
2
(
x
)
,
…
,
R
n
(
x
)
}
\boldsymbol{R}=\left\{R_{1}(x), R_{2}(x), \ldots, R_{n}(x)\right\}
R={R1(x),R2(x),…,Rn(x)},并且
R
\boldsymbol{R}
R 继承了
B
\boldsymbol{B}
B 的许多属性。
R
\boldsymbol{R}
R 由
n
n
n 个形状相同但位置不同的基函数组成。基函数的数量
n
n
n 以及位置参数
a
i
a_{i}
ai 和
b
i
b_{i}
bi 仍然由网格的数量
G
G
G 和跨度参数
k
k
k 决定。
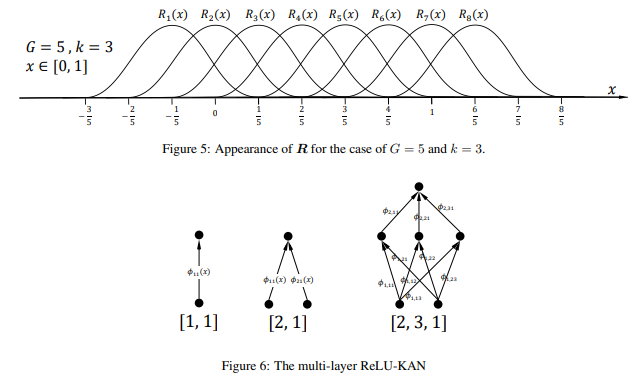
如果我们假设要拟合的函数的定义域为 x ∈ [ 0 , 1 ] x \in[0,1] x∈[0,1],网格的数量为 G G G,跨度参数为 k k k,则样条函数的数量为 n = G + k n=G+k n=G+k。 R i ( x ) R_{i}(x) Ri(x) 的参数 s i = i − k − 1 G s_{i}=\frac{i-k-1}{G} si=Gi−k−1, e i = i G e_{i}=\frac{i}{G} ei=Gi。
例如,图 5 展示了当
G
=
5
G=5
G=5 且
k
=
3
k=3
k=3 时,
R
\boldsymbol{R}
R 的示意图。
ReLU-KAN 层也可以用方程 (5) 来表示,而 ReLU-KAN 对应的 ϕ ( x ) \phi(x) ϕ(x) 去除了偏置函数,并进一步简化为方程 7。
ϕ ( x ) = ∑ i = 1 G + k w i R i ( x ) \phi(x)=\sum_{i=1}^{G+k} w_{i} R_{i}(x) ϕ(x)=∑i=1G+kwiRi(x)
多层 ReLU-KAN 可以用图 6 来表示。在下面的表达式中,我们使用
[
n
1
,
n
2
,
…
,
n
k
]
\left[n_{1}, n_{2}, \ldots, n_{k}\right]
[n1,n2,…,nk] 来表示一个具有
k
−
1
k-1
k−1 层的 ReLU-KAN,其中第
i
i
i 层将第
i
−
1
i-1
i−1 层的输出作为输入。其输入向量的长度为
n
i
n_{i}
ni,输出向量的长度为
n
i
+
1
n_{i+1}
ni+1。
3.2 运算优化
考虑单层ReLU KAN的计算。给定超参数 G G G和 k k k,输入的数量 n n n记作 x = [ x 1 , x 2 , … , x i , … , x n ] \boldsymbol{x}=\left[x^{1}, x^{2}, \ldots, x^{i}, \ldots, x^{n}\right] x=[x1,x2,…,xi,…,xn],以及输出的数量 m m m记作 y = [ y 1 , y 2 , … , y c , … , y m ] \boldsymbol{y}=\left[y^{1}, y^{2}, \ldots, y^{c}, \ldots, y^{m}\right] y=[y1,y2,…,yc,…,ym],我们预先计算起始矩阵 S S S、结束矩阵 E E E和 m m m个权重矩阵 [ W 1 , W 2 , … , W c , … , W m ] \left[W^{1}, W^{2}, \ldots, W^{c}, \ldots, W^{m}\right] [W1,W2,…,Wc,…,Wm],如方程8所示:
S = ( s 1 , 1 s 1 , 2 ⋯ s 1 , G + k s 2 , 1 s 2 , 2 ⋯ s 2 , G + k ⋮ ⋮ ⋱ ⋮ s n , 1 s n , 2 ⋯ s n , G + k ) E = ( e 1 , 1 e 1 , 2 ⋯ e 1 , G + k e 2 , 1 e 2 , 2 ⋯ e 2 , G + k ⋮ ⋮ ⋱ ⋮ e n , 1 e n , 2 ⋯ e n , G + k ) W c = ( w 1 , 1 c w 1 , 2 c ⋯ w 1 , G + k c w 2 , 1 c w 2 , 2 c ⋯ w 2 , G + k c ⋮ ⋮ ⋱ ⋮ w n , 1 c w n , 2 c ⋯ w n , G + k c ) S=\left(\begin{array}{cccc} s_{1,1} & s_{1,2} & \cdots & s_{1, G+k} \\ s_{2,1} & s_{2,2} & \cdots & s_{2, G+k} \\ \vdots & \vdots & \ddots & \vdots \\ s_{n, 1} & s_{n, 2} & \cdots & s_{n, G+k} \end{array}\right) E=\left(\begin{array}{cccc} e_{1,1} & e_{1,2} & \cdots & e_{1, G+k} \\ e_{2,1} & e_{2,2} & \cdots & e_{2, G+k} \\ \vdots & \vdots & \ddots & \vdots \\ e_{n, 1} & e_{n, 2} & \cdots & e_{n, G+k} \end{array}\right) W^{c}=\left(\begin{array}{cccc} w_{1,1}^{c} & w_{1,2}^{c} & \cdots & w_{1, G+k}^{c} \\ w_{2,1}^{c} & w_{2,2}^{c} & \cdots & w_{2, G+k}^{c} \\ \vdots & \vdots & \ddots & \vdots \\ w_{n, 1}^{c} & w_{n, 2}^{c} & \cdots & w_{n, G+k}^{c} \end{array}\right) S= s1,1s2,1⋮sn,1s1,2s2,2⋮sn,2⋯⋯⋱⋯s1,G+ks2,G+k⋮sn,G+k E= e1,1e2,1⋮en,1e1,2e2,2⋮en,2⋯⋯⋱⋯e1,G+ke2,G+k⋮en,G+k Wc= w1,1cw2,1c⋮wn,1cw1,2cw2,2c⋮wn,2c⋯⋯⋱⋯w1,G+kcw2,G+kc⋮wn,G+kc
其中, s i , j = j − k − 1 G s_{i, j}=\frac{j-k-1}{G} si,j=Gj−k−1, e i , j = j G e_{i, j}=\frac{j}{G} ei,j=Gj,且 w i , j c w_{i, j}^{c} wi,jc是一个随机浮点数。
当使用方程6作为基函数时,我们定义一个归一化常数 r = 16 G 4 ( k + 1 ) 4 r=\frac{16 G^{4}}{(k+1)^{4}} r=(k+1)416G4, y c y^{c} yc的计算可以分解为以下矩阵运算:
A = ReLU ( E − x T ) B = ReLU ( x T − S ) D = r × A ⋅ B F = D ⋅ D y c = W c ⊗ F \begin{aligned} A & =\text{ReLU}\left(E-\boldsymbol{x}^{T}\right) \\ B & =\text{ReLU}\left(\boldsymbol{x}^{T}-S\right) \\ D & =r \times A \cdot B \\ F & =D \cdot D \\ y^{c} & =W^{c} \otimes F \end{aligned} ABDFyc=ReLU(E−xT)=ReLU(xT−S)=r×A⋅B=D⋅D=Wc⊗F
其中, A , B , D A, B, D A,B,D 和 F F F 都是中间结果。“ ⋅ \cdot ⋅”表示点积运算。“ ⊗ \otimes ⊗”是深度学习中常用的卷积运算。由于 W c W^{c} Wc 和 F F F 大小相同,方程13将输出一个标量。
方程9到方程12用于计算该层中所有如方程6所示的基函数,这些步骤的结果 F F F可以用方程14描述:
F = ( R 1 ( x 1 ) R 2 ( x 1 ) ⋯ R G + k ( x 1 ) R 1 ( x 2 ) R 2 ( x 2 ) ⋯ R G + k ( x 2 ) ⋮ ⋮ ⋱ ⋮ R 1 ( x n ) R 2 ( x n ) ⋯ R G + k ( x n ) ) F=\left(\begin{array}{cccc} R_{1}\left(x_{1}\right) & R_{2}\left(x_{1}\right) & \cdots & R_{G+k}\left(x_{1}\right) \\ R_{1}\left(x_{2}\right) & R_{2}\left(x_{2}\right) & \cdots & R_{G+k}\left(x_{2}\right) \\ \vdots & \vdots & \ddots & \vdots \\ R_{1}\left(x_{n}\right) & R_{2}\left(x_{n}\right) & \cdots & R_{G+k}\left(x_{n}\right) \end{array}\right) F= R1(x1)R1(x2)⋮R1(xn)R2(x1)R2(x2)⋮R2(xn)⋯⋯⋱⋯RG+k(x1)RG+k(x2)⋮RG+k(xn)
在实际的代码实现中,我们可以直接使用卷积层来实现方程13的计算。我们给出了基于PyTorch的ReLU-KAN层的Python代码,如图7所示。这段代码非常简单,不需要占用太多空间。
4、实验
实验评估分为三个主要部分。首先,我们在GPU和CPU环境中比较KAN和ReLU-KAN的训练速度。其次,我们在相同的参数设置下评估两种模型的拟合能力和收敛速度。最后,我们利用ReLU-KAN来复制KAN在灾难性遗忘背景下的性能。
4.1、训练速度比较
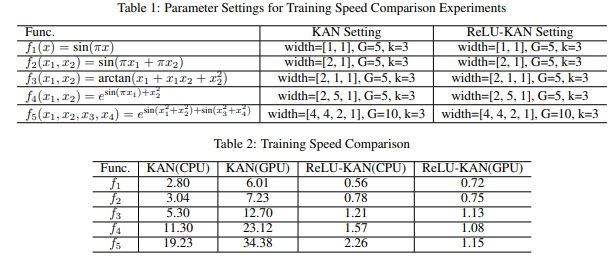
我们选择了一个大小为5的函数集来比较KAN和ReLU-KAN的训练速度。KAN和ReLU-KAN的参数设置如表1所示。
训练过程使用PyTorch框架进行。我们采用Adam优化器进行优化,并将训练集大小设置为1000个样本。所有模型都进行了500次迭代训练。表2总结了KAN和ReLU-KAN在GPU和CPU环境下的训练时间。
根据表2中给出的结果,可以得出以下结论:
- ReLU-KAN比KAN更快:在所有比较中,ReLU-KAN都比KAN消耗的时间显著更少。
- ReLU-KAN的训练随复杂度增加效率更高:随着模型架构变得更加复杂,KAN和ReLU-KAN的训练时间都会增加。然而,ReLU-KAN的时间消耗增加量远小于KAN。
- ReLU-KAN在GPU上的速度优势随模型复杂度增加而增大:随着模型复杂度的增加,ReLU-KAN在GPU上相对于CPU的速度优势更加明显。对于单层模型( f 1 f_{1} f1和 f 2 f_{2} f2),ReLU-KAN比KAN快4倍。对于2层模型( f 3 f_{3} f3和 f 4 f_{4} f4),速度差异在5到10倍之间,而对于3层模型( f 5 f_{5} f5),速度差异接近20倍。
4.2、拟合能力比较
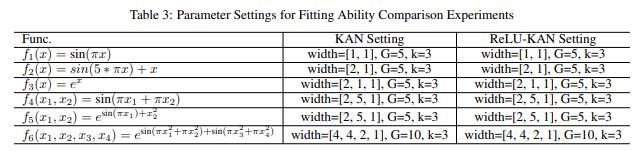
然后,我们在三个一元函数和三个多元函数上比较KAN和ReLU-KAN的拟合能力,每个函数都使用表3中所示的参数设置。
为了评估KAN和ReLU-KAN的性能,我们采用均方误差(MSE)损失函数作为评价指标,并利用Adam优化器进行优化。最大迭代次数设置为1000。
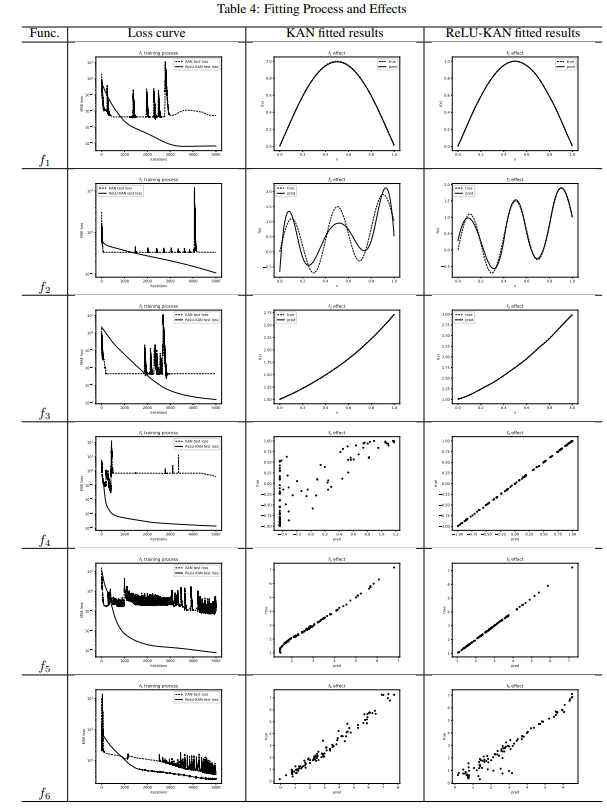
为了可视化两个模型的迭代过程,我们绘制了它们的损失曲线。我们可以通过以下方式可视化拟合效果:对于一元函数
f
1
f_{1}
f1、
f
2
f_{2}
f2和
f
3
f_{3}
f3,我们直接将它们的原始
f
(
x
)
f(x)
f(x)曲线与拟合曲线绘制在一起,从而清晰地表示它们的拟合性能。对于多元函数
f
4
f_{4}
f4、
f
5
f_{5}
f5和
f
6
f_{6}
f6,我们生成了预测值与真实值的散点图。散点越接近直线
p
r
e
d
=
t
r
u
e
pred = true
pred=true,表示拟合性能越好。
表4中的结果表明,在给定相同的网络结构和规模下,ReLU-KAN展示了更稳定的训练过程,并实现了更高的拟合精度。这一优势在多层网络中尤为明显,特别是在拟合像 f 2 f_{2} f2这样变化频率较高的函数时。在这些情况下,ReLU-KAN表现出了卓越的拟合能力。
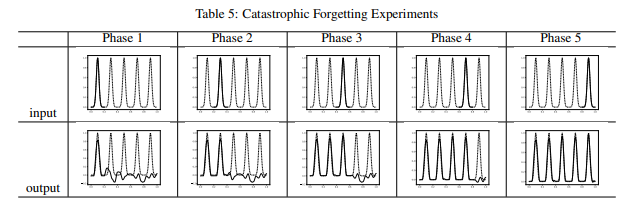
4.3、ReLU-KAN 避免灾难性遗忘
由于ReLU-KAN与KAN具有相似的基础函数结构,因此预期ReLU-KAN能够继承KAN对灾难性遗忘的抵抗力。为了验证这一点,我们进行了一个简单的实验。
与为KAN设计的实验类似,目标函数具有五个峰值。在训练过程中,模型每次只接收一个峰值的数据。下图展示了ReLU-KAN在每次训练迭代后的拟合曲线。
如表5所示,ReLU-KAN同样具有避免灾难性遗忘的能力。
5、总结与展望
本文介绍了一种名为ReLU-KAN的新型架构,该架构使用新型基础函数替换了KAN中的B样条。此外,ReLU-KAN实现了全矩阵运算,显著提高了训练速度。实验结果表明,ReLU-KAN在训练速度、拟合能力和稳定性方面均优于KAN。在未来的工作中,我们计划将ReLU-KAN应用于卷积和Transformer架构中,以研究其在不牺牲模型性能的情况下减少参数的潜力。
致谢
本工作得到了中国国家自然科学基金(62006110)、湖南省自然科学基金(2024JJ7428, 2023JJ30518)、上海市自然科学基金(No.23ZR1429300)和湖南省教育厅科学研究项目(22C0229)的部分资助。