Bootstrap

C++数据结构之栈（详解） 

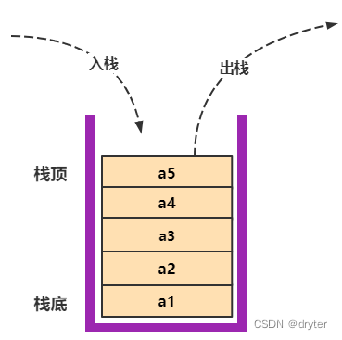
栈（stack）是线性表的一种，其特点是只能在一端进行插入和删除操作（也称top端、栈顶端）,因此具有先进后出或者后进先出的特性（先入栈的数据只能后出栈，而后入栈的数据需要先出来），通常可以吧栈理解为受限的线性表。
把栈比喻成一个木桶容器，栈有两端，允许插入和删除的一端称为栈顶（top），也就是桶口，或者线性表的表尾，而另一端称为栈底（bottom）也就是栈底，或者称为线性表的表头。
向栈中插入元素称为入栈或者进栈，从栈中删除元素称为出栈。除能够在表尾插入和删除数据外，对于栈这种数据结构，在栈的其他位置插入或删除都不被允许。
不包含任何数据的栈称为空栈（空线性表）。栈也被称为先进后出（Last In Last Out：LIFO）的线性表，这意味着最后放入到栈里的数据（插入元素）只能最先被拿出来（删除数据）
用栈存储数据的示意图，如下：

在这里插入图片描述

1.栈的书匈奴存储（顺序栈）


能保存10个元素的顺序栈（图）
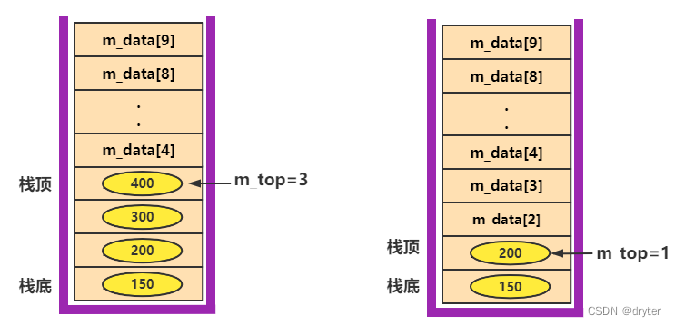
在这里插入图片描述入栈出栈示意图

所谓的顺序栈，就是顺序存储（用一段连续的内存空间一次存储）栈中的数据。
顺序栈实现代码，如下：

#include<iostream>

using  namespace std;

#define InitSize 10
#define IncSize 5

template<typename T>
class SeqStack 
{
public:
	SeqStack(int length = InitSize);
	~SeqStack();
	
public:
	bool Push(const T& e);//入栈
	bool Pop(T& e);//出栈
	bool GetTop(T& e);//读取栈顶元素
	void DispList();//输出栈中所有元素
	int ListLength();//获取顺序栈的长度(栈中元素个数)
	bool IsEmpty();//判断栈是否为空
	bool IsFull();//判断栈是否已满

private:
	void IncreaseSize();//当顺序栈已满时，可以调用此函数进行扩容

private:
	T* m_data;//顺序栈的元素值
	int m_maxsize;//动态数组最大容量
	int m_top;//栈顶指针（用作数组下标）
};

template<typename T>
SeqStack<T>::SeqStack(int length) 
{
	m_data = new T[length];//为一维数组分配内存控件
	m_maxsize = length;
	m_top = -1;//空栈，栈的初始化位置为0
}

template<typename T>
SeqStack<T>::~SeqStack()
{
	delete[] m_data;
}

template<typename T>
bool SeqStack<T>::Push(const T& e)
{
	if (IsFull() == true) 
	{
		IncreaseSize();//扩容
	}
	m_top++;
	m_data[m_top] = e;
	return true;
}

template<typename T>
void SeqStack<T>::IncreaseSize() 
{
	T* p = m_data;
	m_data = new T[m_maxsize + IncSize];
	for (int i = 0; i <= m_top; i++) 
	{
		m_data[i] = p[i];
	}
	m_maxsize = m_maxsize + IncSize;
	delete[] p;
}

template<typename T>
bool SeqStack<T>::Pop(T& e) 
{
	if (IsEmpty() == true) 
	{
		cout << "当前栈为空，无法进行出栈操作" << endl;
		return false;
	}
	e = m_data[m_top];
	m_top--;
	return true;
}

template<typename T>
bool SeqStack<T>::GetTop(T& e) 
{
	if (IsEmpty == true) 
	{
		cout << "当前栈为空，无法进行取栈顶元素操作" << endl;
		return false;
	}
	e = m_data[m_top];
	return true;
}

template<typename T>
void SeqStack<T>::DispList() 
{
	for (int i = m_top;i >= 0; --i) 
	{
		cout << m_data[i] << " " << endl;
	}
	cout << endl;
}

template<typename T>
int SeqStack<T>::ListLength() 
{
	return m_top+1;
}

template<typename T>
bool SeqStack<T>::IsEmpty() 
{
	if (m_top == -1) 
	{
		return true;
	}
	return false;
}

template<typename T>
bool SeqStack<T>::IsFull() 
{
	if (m_top >= m_maxsize - 1) 
	{
		return true;
	}
	return false;
}

int main(int argc,char** argv) 
{
	SeqStack<int> seqstack(10);
	seqstack.Push(10);
	seqstack.Push(20);
	seqstack.Push(30);
	seqstack.Push(40);
	seqstack.Push(50);
	int num = 0;
	seqstack.Pop(num);
	seqstack.Pop(num);
	seqstack.DispList();
}

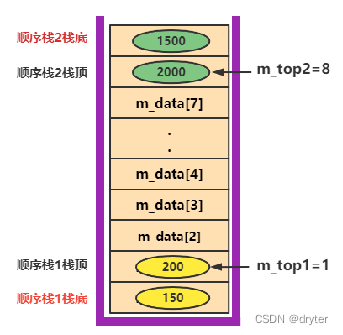
2.共享栈

所谓共享栈其实是两个顺序栈共享存储空间。顺序栈的一个比较大的缺陷是保存数据初始尺寸不好确定，太大浪费内存空间，如果太小，则存满数据后再入新栈数据就需要扩容。

共享栈存储示意图
共享栈存储示意图

共享栈的实现代码，如下：

#include <iostream>

using namespace std;

#define InitSize 10
#define IncSize 5

template<typename T>
class SharedStack
{
public:
	SharedStack(int length = InitSize);
	~SharedStack();

public:
	bool Push(int stackNum,const T& e);//入栈
	bool Pop(int stackNum,T& e);//出栈
	void DispList();//输出栈中所有元素
	int ListLength();//获取顺序栈的长度(栈中元素个数)
	bool IsEmpty();//判断栈是否为空
	bool IsFull();//判断栈是否已满

private:
	void IncreaseSize();//当顺序栈已满时，可以调用此函数进行扩容

private:
	T* m_data;//顺序栈的元素值
	int m_maxsize;//动态数组最大容量
	int m_top1;//栈1栈顶指针（用作数组下标）
	int m_top2;//栈2栈顶指针（用作数组下标）
};

template<typename T>
SharedStack<T>::SharedStack(int length) 
{
	m_data = new T[length];
	m_maxsize = length;
	m_top1 = -1;
	m_top2 = length;
}

template<typename T>
SharedStack<T>::~SharedStack()
{
	delete[] m_data;
}

template<typename T>
bool SharedStack<T>::IsFull() 
{
	if ((m_top + 1) == m_top2) 
	{
		return true;
	}
	return false;
}

template<typename T>
bool SharedStack<T>::Push(int StackNum,const T& e) 
{
	if (IsFull() == true) 
	{
		cout << "共享栈满了，不能再进行入栈操作" << endl;
		return false;
	}
	if (StackNum == 1) 
	{
		m_top1++;
		m_data[m_top1] = e;
	}
	else 
	{
		m_top2--;
		m_data[m_top2] = e;
	}
	return true;
}

template<typename T>
void SharedStack<T>::IncreaseSize() 
{
	T* p = m_data;
	m_data = new T[m_maxsize + IncSize];
	for (int i = 0; i <= m_top2;i++) 
	{
		m_data[i] = p[i];
	}
	m_top2 += IncSize;
	delete[] p;
}

template<typename T>
bool SharedStack<T>::Pop(int stackNum, T& e) 
{
	if (stackNum == 1) 
	{
		if (m_top1 == -1) 
		{
			cout << "当前顺序栈1为空，不能进行出栈操作" << endl;
			return false;
		}
		e = m_data[m_top1];
		m_top1--;
	}
	else
	{
		if (m_top2 == m_maxsize) 
		{
			cout << "顺序栈2为空，无法进行出栈操作" << endl;
			return false;
		}
		e = m_data[m_top2];
		m_top2++;
	}
	return true;
}

template<typename T>
int SharedStack<T>::ListLength()
{
	return m_maxsize-m_top2+m_top1+1;
}

template<typename T>
void SharedStack<T>::DispList()
{
	for (int i = 0; i <= m_top1;i++) 
	{
		cout << m_data[i] << " ";
	}
	for (int i = m_maxsize;i >= m_top2) 
	{
		cout << m_data[i] << " ";
	}
	cout << endl;
}

template<typename T>
bool SharedStack<T>::IsEmpty()
{
	if ((m_top1 == -1) && (m_top2 == m_maxsize)) 
	{
		return true;
	}
	return false;
}

3.栈的链式存储（链式栈）

链式栈：使用链式存储的方式来实现栈。
实现代码如下：

#include<iostream>

using namespace std;

template<typename T>
struct StackNode 
{
	T data;//数据域，存放数据
	StackNode<T>* next;//指针域，指向下一个节点
};

template<typename T>
class LinkStack
{
public:
	LinkStack();
	~LinkStack();

public:
	bool Push(const T& e);//入栈
	bool Pop(T& e);//出栈
	bool GetTop(T& e);//读取栈顶元素
	void DispList();//输出栈中所有元素
	int ListLength();//获取顺序栈的长度(栈中元素个数)
	bool Empty();//判断栈是否为空

private:
	StackNode<T>* m_top;//栈顶指针
	int m_length;//链式栈元素个数
};

template<typename T>
LinkStack<T>::LinkStack() 
{
	m_top = nullptr;
	m_length = 0;
}

template<typename T>
LinkStack<T>::~LinkStack() 
{
	T tmpvalue = { 0 };
	while (Pop(tmpvalue) == true) {}
}

template<typename T>
bool LinkStack<T>::Push(const T& e) 
{
	StackNode<T>* node = new StackNode<T>;
	node->data = e;
	node->next = m_top;
	m_top = node;
	m_length++;
	return true;
}

template<typename T>
bool LinkStack<T>::Pop(T& e) 
{
	if (Empty() == true) 
	{
		return false;
	}
	StackNode<T>* p_willdel = m_top;
	m_top = m_top->next;
	m_length--;
	e = m_top->data;
	delete p_willdel;
	return true;
}

template<typename T>
bool LinkStack<T>::GetTop(T& e) 
{
	if (Empty() == true) 
	{
		return false;
	}
	e = m_top->data;
	return true;
}

template<typename T>
void LinkStack<T>::DispList() 
{
	if (Empty == true) 
	{
		cout << "链式栈为空，无法输出任何数据" << endl;
		return;
	}
	StackNode<T>* p = m_top;
	while (p != nullptr) 
	{
		cout << p->data << " ";
		p = p->next;
	}
	cout << endl;
}

template<typename T>
bool LinkStack<T>::Empty() 
{
	if (m_top == nullptr) 
	{
		return true;
	}
	return false;
}

4.栈的实际应用–逆波兰表达式
逆波兰表达式即后缀表达式，利用栈存储的先进后出，后进先出特性。
力扣题号150题：逆波兰求值。

class Solution 
{
public:
	int evalRPN(vector<string>& tokens) 
	{
		stack<int> st;
		for (int i = 0; i < tokens.size(); i++) 
		{
			if (tokens[i] == "+" || tokens[i] == "-" || tokens[i] == "*" || tokens[i] == "/")
			{
				int num1 = st.top();
				st.pop();
				int num2 = st.top();
				st.pop();
				if (tokens[i] == "+")
				{
					st.push(num2+num1);
				}
				if (tokens[i] == "+")
				{
					st.push(num2 - num1);
				}
				if (tokens[i] == "*")
				{
					st.push(num2 * num1);
				}
				if (tokens[i] == "/")
				{
					st.push(num2 / num1);
				}
			}
			else 
			{
				st.push(stoi(tokens[i]));
			}
		}
		int result = st.top();
		st.pop();
		return result;
	}
};

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
算法 topN
Java-19 深入浅出 MyBatis - 用到的设计模式 源码剖析 代理设计模式
Linux云计算 |【第五阶段】ARCHITECTURE-DAY5
Redis的缓存穿透、缓存击穿、缓存雪崩
meta标签 meta http-equiv = “X-UA-Compatible“ content = “IE=edge,chrome=1“ /＞解析
visualvm工具远程对linux服务器上的JVM虚拟机进行监控与调优方案
【信息安全管理与评估】2023年全国职业院校技能大赛赛题第05套
11.组合模式设计思想
Scrapy框架详解
简单SpringCloud项目（大致的后台流程）
;