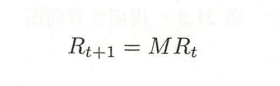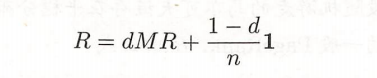Python实现PageRank计算

Python实现PageRank算法

利用python来计算统计学习方法PageRank算法例题。

PageRank介绍

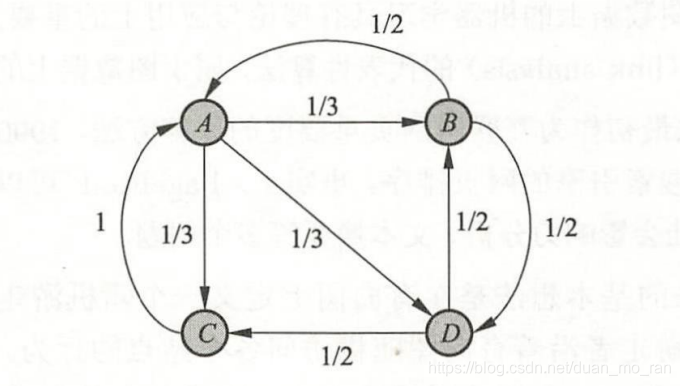
PageRank算法是图的链接分析的代表性算法，属于图数据上的无监督学习方法。其基本想法是在一个有向图上定义一个随机游走模型，即一阶马尔科夫链，描述随机游走者沿着有向图随机访问各个结点的行为。

PageRank的基本定义

在这里插入图片描述
计算可以在互联网的有向图上进行，通常是一个迭代过程，先假设一个初始分布，通过迭代，不断计算所有网页的PR值，直到收敛为止。
由以上的有向图可以定义随机游走模型，可以得到转移矩阵：

随机游走在某个时刻t访问各个结点的概率分布就是马尔科夫链在时刻t的分布，可以用一个n维列向量Rt表示，那么在时刻t+1访问各个结点的Rt+1满足：
在这里插入图片描述
可以根据之上得到的转移矩阵，和定义初始分向量，利用python计算得到最后趋于收敛的PR值。

import numpy as np
from fractions import Fraction
np.set_printoptions(formatter={'all':lambda x: str(Fraction(x).limit_denominator())}) #格式化 保留分数，不至于精度丢失
M = np.array([[0,1/2,1,0],[1/3,0,0,1/2],[1/3,0,0,1/2],[1/3,1/2,0,0]])   #根据有向图得出的转移矩阵
R = np.array([1/4,1/4,1/4,1/4]).reshape(4,1)  #初始R0
def diedai(M,R):     #定义一个迭代函数，直至MR=R时，输出R
    count = 0
    while(True):
        R_1 = np.dot(M,R)
        if((R_1 == R).any()):   #判断两个数组是否相等
            print(R_1)
            print('迭代次数为：',count)
            break
        else:
            R = np.copy(R_1)
            count +=1
diedai(M,R)

运行结果如下：

[[1/3]
 [2/9]
 [2/9]
 [2/9]]
迭代次数为： 51

PageRank的一般定义

PageRank的一般定义的想法是在基本定义的基础上导入平滑项。
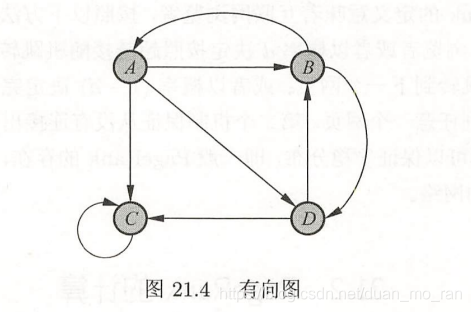
因为可能会存在没有出链的结，或者存在一些孤立的结点，即这个马尔科夫链未必具有平稳分布。利用基本定义的公式会随着时间推移，各个结点的概率会为0，所以引入阻尼因子。计算公式变为了：
在这里插入图片描述
d为阻尼因子（0<=d<=1)。R是n维向量。

利用python编程验证得到在2345次的时候，结点的概率就有为0的：

M = np.array([[0,1/2,0,0],[1/3,0,0,1/2],[1/3,0,0,1/2],[1/3,1/2,0,0]])   #根据有向图得出的转移矩阵
R = np.array([1/4,1/4,1/4,1/4]).reshape(4,1)  #初始R0
R_0 = np.array([0,0,0,0]).reshape(4,1)
def diedai(M,R):     #定义一个迭代函数，直至MR = R时，输出R
    count =0 
    while(True):
        R_1 = np.dot(M,R)
        if((R_1 == R).any() | (R_1 == R_0).any()):   #判断两个数组是否相等
            print(R_1)
            print('迭代次数为：',count)
            break
        else:
            R = np.copy(R_1)
            count +=1
        #print(R_1)
diedai(M,R)

[[0]
 [0]
 [0]
 [0]]
迭代次数为： 2345

PageRank的计算

1、迭代算法

利用迭代法实现一般定义的公式。

M=[[0,1/2,0,0],[1/3,0,0,1/2],[1/3,0,1,1/2],[1/3,1/2,0,0]]
d = 4/5
dM = np.dot(d,M)
I = np.ones(4)
I_0 = np.dot((1-d)/4,I)
R_0 = [1/4,1/4,1/4,1/4]
def diedai(M,R,I_0):
    count = 0
    while(True):
        R_1 = np.dot(M,R)+I_0
        if((R_1 == R).any()):   #判断两个数组是否相等  R = R_t+1,停止迭代
            print(R_1)
            print('迭代次数为：',count)
            break
        else:
            R = np.copy(R_1)
            count +=1
        #print(R_1)
diedai(dM,R_0,I_0)

[45/592 57/592 328943/683278 57/592]
迭代次数为： 67

2、幂法

在这里插入图片描述
利用python编程实现，以及结果如下：

M = [[0,0,1],[1/2,0,0],[1/2,1,0]]
x_0 = np.array([1,1,1])
#计算有向图的一般转移矩阵A
d = 0.85
E = np.ones((3,3))
A = np.dot(d,M)+np.dot((1-d)/3,E)
min_delta=0.0000001  #精度

def getPR(A,x_0,min_delta):
    count = 0
    while(True):  
        y = np.dot(A,x_0)
        x_1 = np.dot(1/max(y),y)
        e = max(np.abs(x_1-x_0))
        if(e < min_delta):
            print(x_0)
            print('迭代次数为：',count)
            break
        x_0 = x_1
        count =count+1
        #print(e)
getPR(A,x_0,min_delta)

[768282/787321 383027/708600 1]
迭代次数为： 31

由输出的平稳收敛的次数可知，相对而言幂法会好一些，所以计算PR值时多数使用幂法。

PageRank算法的缺点

这是一个天才的算法，原理简单但效果惊人。然而，PageRank算法还是有一些弊端。所以其实google本身也在不断改进这个算法。
第一，没有区分站内导航链接。很多网站的首页都有很多对站内其他页面的链接，称为站内导航链接。这些链接与不同网站之间的链接相比，肯定是后者更能体现PageRank值的传递关系。
第二，没有过滤广告链接和功能链接（例如常见的“分享到微博”）。这些链接通常没有什么实际价值，前者链接到广告页面，后者常常链接到某个社交网站首页。
第三，对新网页不友好。一个新网页的一般入链相对较少，即使它的内容的质量很高，要成为一个高PR值的页面仍需要很长时间的推广。