Mojo 学习 —— SIMD

Mojo 使用 SIMD 类型作为其数字类型的基础。一个 SIMD 对象表示一个由硬件向量元素支持的小的向量，也就是一个固定大小的值数组，可以放入处理器的寄存器中。

SIMD 结构体

SIMD 向量由两个 parameter 定义：

• type：DType 类型，指定向量元素的类型
• size：Int 类型，向量的长度，必须是正数且为 2 的整数幂

SIMD 结构体定义了很多对象方法，便于我们对其进行操作，此外在 math 模块中，还定义了丰富的函数，方便进行数学计算。

创建 SIMD 对象

例如，定义一个 SIMD 类型的值，默认初始化为 0，可以为所有元素指定同一初始值或一次性指定所有元素的值

print(SIMD[DType.int8, 2]())
# [0, 0]
print(SIMD[DType.int8, 2](1))
# [1, 1]
print(SIMD[DType.int8, 2](1, 2))
# [1, 2]
print(SIMD[DType.float16, 2](3.14))
# [3.140625, 3.140625]

向量访问

获取向量中的某个元素并设置它的值

var a = SIMD[DType.int8, 2](0)
print(a[0])
a[0] = 1
print(a)

也可以使用 slice 方法，获取向量切片，其中 offset 设置切片开始的位置，默认为 0

var a = SIMD[DType.uint8, 4](9, 5, 2, 7)
print(a.slice[2]())
print(a.slice[2, offset=2]())
# [9, 5]
# [2, 7]

类型转换

使用 cast 方法，可以将对象转换为其他 DType 类型。例如

var a = SIMD[DType.uint8, 4](9, 5, 2, 7)
print(a.cast[DType.bool]())
print(a.cast[DType.float16]())
# [True, True, True, True]
# [9.0, 5.0, 2.0, 7.0]

算术运算

基本上所有单个数值支持的运算，SIMD 也支持。因为单个数可以看成是长度为 1 的 SIMD 类型，且基本支持原地修改操作，如 +=，-= 等。

对 SIMD 进行算术运算，可以是两个类型相同的对象进行运算（对应位置的元素之间执行运算），也可以是和一个值进行运算（广播）。例如

var a = SIMD[DType.int8, 2](0)
print(a + 2)
var b = SIMD[DType.int8, 2](0)
if a or b:
    print('TRUE')
a += 2
b += 3
print(a + b)
print(a * b)
# [2, 2]
# [5, 5]
# [6, 6]

由于数据类型具有大小限制，当执行加、减、乘法运算时，可能会导致数值溢出的情况，可以使用更安全的方法。例如

var a = SIMD[DType.uint8, 2](255)
var b = SIMD[DType.uint8, 2](100)
var c = a.add_with_overflow(b)
print('add:', c[0])
print('bool:', c[1])
# add: [99, 99]
# bool: [True, True]

返回一个 Tuple 类型，第一个为对应位置的计算结果，第二个元素为每个位置是否发生了溢出。

还有类似的 sub_with_overflow 和 mul_with_overflow。

除法运算

var a = SIMD[DType.float16, 4](9, 5, 2, 7)
var b = SIMD[DType.float16, 4](3, 7, 8, 0)
print(a / b)
print(a // b)
# [3.0, 0.71435546875, 0.25, inf]
# [3.0, 0.0, 0.0, inf]

取余

print(a % b)
print(a % 2)
# [0.0, 5.0, 2.0, nan]
# [1.0, 1.0, 0.0, 1.0]

幂运算

var a = SIMD[DType.int32, 4](9, 5, 2, 7)
var b = SIMD[DType.int32, 4](3, 7, 8, 0)
print(a ** b)
print(a ** 2)
# [729, 78125, 256, 1]
# [81, 25, 4, 49]

比较运算

比较两个 SIMD 对象的值

var a = SIMD[DType.uint8, 4](9, 5, 2, 7)
var b = SIMD[DType.uint8, 4](3, 7, 8, 0)
print(a > b)
print(a >= b)
print(a.max(b))
print(a.min(b))
# [True, False, False, True]
# [True, False, False, True]
# [9, 7, 8, 7]
# [3, 5, 2, 0]

位运算

对整数进行位运算，相当于逐元素的位运算

var a = SIMD[DType.uint8, 4](9, 5, 2, 7)
var b = SIMD[DType.uint8, 4](3, 7, 8, 0)
print(a & b)
print(a | b)
print(a ^ b)
print(~a)
print(9 & 3, 9 | 3, 9 ^ 3)
# [1, 5, 0, 0]
# [11, 7, 10, 7]
# [10, 2, 10, 7]
# [246, 250, 253, 248]
# 1 11 10

逻辑运算

比较两个布尔向量

var a = SIMD[DType.bool, 4](True, False, True, False)
var b = SIMD[DType.bool, 4](False, False, True, True)
print(a & b)
print(a | b)
print(a ^ b)
print(~a)
# [False, False, True, False]
# [True, False, True, True]
# [True, False, False, True]
# [False, True, False, True]

累积运算

我们可以计算元素的累加和、累乘等，还可以使用累积的方式计算最大值最值

var a = SIMD[DType.int64, 4](6, 3, 9, 4)
print('Sum:', a.reduce_add())   # 22
print('Prod:', a.reduce_mul())  # 648
print('Max:', a.reduce_max())   # 9
print('Min:', a.reduce_min())   # 3

还可以判断元素是否全为真或存在真。例如

var a = SIMD[DType.bool, 4](True, True, False, True)
print(a.reduce_and())  # False
print(a.reduce_or())   # True
# 使用可以转换为 bool 类型的值
var b = SIMD[DType.uint8, 4](3, 0, 6, 0)
print(a.reduce_or())   # True
var c = a | b.cast[DType.bool]()
print(c). # [True, True, True, True]
print(c.reduce_and())  # True

还可以自定义累积运算的函数

fn main():
    @parameter
    fn func[type: DType, size: Int](x: SIMD[type, size], y: SIMD[type, size]) -> SIMD[type, size]:
        print(x, y)
        return x.max(y)
    var a = SIMD[DType.int8, 8](9, 5, 8, 7, 1, 5, 4, 3)
    print(a.reduce[func, 2]())
# [9, 5, 8, 7] [1, 5, 4, 3]
# [9, 5] [8, 7]
# [9, 7]

从输出结果来看，累积操作使用的是二分法

移动元素

我们可以对元素进行整体的平移操作，平移可以是循环移动（即头尾位置连通）。例如

var a = SIMD[DType.uint8, 4](3, 0, 6, 0)
print(a.rotate_left[1]())   # 向左移动 1 个元素
print(a.rotate_right[2]())  # 向右移动 2 个元素
# [0, 6, 0, 3]
# [6, 0, 3, 0]

也可以平移后将空位置补零

print(a.shift_left[2]())
print(a.shift_right[1]())
# [6, 0, 0, 0]
# [0, 3, 0, 6]

合并与拆分

合并两个 SIMD 对象

var a = SIMD[DType.uint8, 4](3, 0, 6, 0)
var b = SIMD[DType.uint8, 4](9, 5, 2, 7)
print(a.join(b))        # 按顺序合并
print(a.interleave(b))  # 交叉合并
# [3, 0, 6, 0, 9, 5, 2, 7]
# [3, 9, 0, 5, 6, 2, 0, 7]

将一个 SIMD 按奇偶位置拆分为两个 SIMD 对象，返回一个长度为 2 的 Tuple

var c = SIMD[DType.uint8, 8](3, 9, 0, 5, 6, 2, 0, 7)
var t = c.deinterleave()
print(t[0])
print(t[1])

替换元素

使用 insert 可以替换指定区间内的值。例如

var a = SIMD[DType.uint8, 4](3, 0, 6, 0)
var b = SIMD[DType.uint8, 4](9, 5, 2, 7)
print(a.insert[](b))
print(a.insert[offset=2](b.slice[2]()))
# [9, 5, 2, 7]
# [3, 0, 9, 5]

我感觉这个操作应该叫 replace 而不是 insert，offset + input_width 不能超过原始向量的长度

或者使用 select 根据元素是否为真，来选择要替换的值

var a = SIMD[DType.bool, 4](True, False, True, False)
var true_case = SIMD[DType.uint8, 4](3, 0, 6, 0)
var false_case = SIMD[DType.uint8, 4](9, 5, 2, 7)
print(a.select(true_case, false_case))
# [3, 5, 6, 7]

math 包

math 包中提供了一些用于计算的函数，主要有四个子模块

• bit：位运算操作
• math：常用的数学计算
• polynomial：多项式计算
• limit：返回类型的无穷值

位运算

bit 子模块中提供了几个位操作函数。包括

• ctlz：计算前导零的个数

print(ctlz(10))
print(ctlz(SIMD[DType.uint8, 1](10)))
# 60
# 4

• cttz：计算后置 0 的个数

from math.bit import cttz

print(cttz(1))  # 0
print(cttz(4))  # 2

• select：同上面的对象 select 方法
• bitreverse：反转整数值的位模式

from math.bit import bitreverse

var a = SIMD[DType.uint8, 4](9, 5, 2, 7)
print(bitreverse(a))
# [144, 160, 64, 224]

• bswap：交换整数的字节顺序。比如 int16 位有两个字节 1|2，将高低位的字节交换，字节顺序变成 2|1。

from math.bit import bswap

var a = SIMD[DType.int16, 4](9, 5, 2, 7)
print(bswap(a))
# [2304, 1280, 512, 1792]

• ctpop: 计算字节中 1 的个数

from math.bit import ctpop

var a = SIMD[DType.int16, 4](9, 5, 2, 7)
print(ctpop(a))
# [2, 2, 1, 3]

• bit_not: 按位取反

from math.bit import bit_not

var a = SIMD[DType.int16, 4](9, 5, 2, 7)
print(bit_not(a))
# [-10, -6, -3, -8]

• bit_and: 按位与

from math.bit import bit_and

var a = SIMD[DType.int16, 4](9, 5, 2, 7)
var b = SIMD[DType.int16, 4](3, 0, 6, 0)
print(bit_and(a, b))
# [1, 0, 2, 0]

• bit_length: 计算表示一个整数所需的字节位数

from math.bit import bit_length

var a = SIMD[DType.int16, 4](9, 5, 2, 7)
print(bit_length(a))
# [4, 3, 2, 3]

数学计算

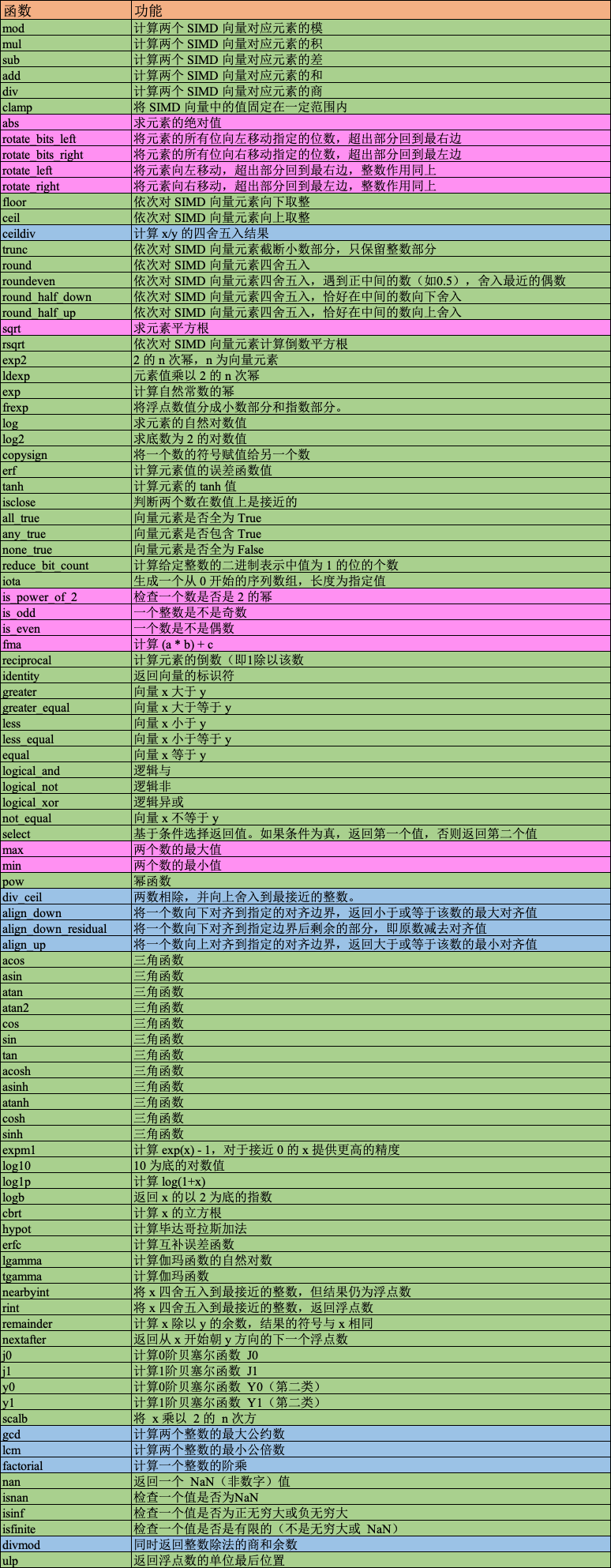
math 子模块中提供了非常多的数学计算函数，其中有很多在前面的对象方法中已经介绍过了，就不再赘述。

下表列出的函数中，绿色标注的为 SIMD 类型可用，粉色为 SIMD 和 Int 共用，蓝色只能用于 Int

import math

fn main():
    var a = SIMD[DType.float64, 4](4.3, 5.5, 6.7, 0.1)
    var b = SIMD[DType.float64, 4](6.8, 5.9, 3.1, 2.5)
    print(math.floor(a))     # 向下取整
    print(math.hypot(a, b))  # 毕达哥拉斯加法
    print(math.cbrt(a))      # 立方根
    print(math.log1p(a))     # log(a+1)
    print(math.exp2(b))      # 2^b
# [4.0, 5.0, 6.0, 0.0]
# [8.0454956342042721, 8.0659779320303127, 7.3824115301167001, 2.5019992006393608]
# [1.6261333316791688, 1.7651741676630317, 1.8852036310209863, 0.46415888336127786]
# [1.6677068205580761, 1.8718021769015913, 2.0412203288596382, 0.095310179804324865]
# [111.43112226071672, 59.71431714149093, 8.5741823343891532, 5.6568474748336897]

多项式计算

计算多项式的值，结果有点奇怪，method 设置为 0(Horner) 和 1(Estrin) 计算出来的结果不一样

from math.polynomial import polynomial_evaluate

fn main():
    var a = SIMD[DType.int64, 4](2, 3, 1, 1)
    alias coefficients = List(
        SIMD[DType.int64, 4](3, 2, -5, 7),
    )
    print(polynomial_evaluate[DType.int64, 4, coefficients, method=0](a))
# [9, 8, -10, 14]

limit

主要用于获取 DType 类型的无穷值或能表示的最大值和最小值

from math.limit import inf, neginf, max_finite, min_finite

fn main():
    print(inf[DType.float64]())     # 必须用浮点数
    print(neginf[DType.float16]())  # 必须用浮点数
    print(max_finite[DType.int64]())
    print(min_finite[DType.int64]())
# inf
# -inf
# 9223372036854775807
# -9223372036854775808