在计算机的世界里，一切信息最终都会转化为二进制数字来存储和处理。而原码、反码、补码，正是计算机内部处理这些二进制数据的核心概念。

别担心，即便你是一位编程小白，本文将用最通俗易懂的方式，带你深入理解这些看似复杂实则有趣的计算机基础知识。

一，原码

1，什么是原码？

原码，简单来说，就是直接将一个数转换成二进制形式表示，包括符号位。

在计算机中，通常用最高位作为符号位，0表示正数，1表示负数。

比如，+5的8位原码是00000101，而-5的8位原码则是10000101。

思考题：
基本数据类型中，byte类型占用一个字节，那么其表示的数据范围是多少？

byte是有符号整数，所以最高位是符号位，有效数字位只有7位，用二进制原码表示其范围为：11111111 ~ 01111111，换算成二进制是-127 ~ 127。但是，这个答案，对吗？

2，原码的硬伤：搞不定负数的加减法

下面，以byte类型为例，分析负数原码的加法遇到的问题。

因为最高位是符号位，1表示负数，0表示正数，所以对于数字0，就有正0和负0的区分，负0的二进制如下：

接下来，我们完成一个小学一年级的数学题：-1 + 1 = ？

毫无疑问，答案应该是0。

但是如果用原码计算的话，-1的原码是：

-1+1=10000001 + 1 = 10000010 = -2

即，用原码计算表达式-1 + 1 的得到的结果-2，这显然错误的。

也就是说，原码搞不定减法，但是我们能发现一些规律，观察下面几个简单的负数加法：
-1+1= 10000001 + 1 =-2
-2+1= 10000010 + 1 =-3
-3+1= 10000011 + 1 =-4
-4+1= 10000100 + 1 =-5

如下图，在坐标轴上，-1+1后的结果本应是在-1的基础上向右移动一个单位距离(到0刻度)，原码计算的结果实际上是向左移动了一个单位(到-2刻度)。

得出了一个非常重要的结论：

• 对负数原码加1计算的结果实际上相当于这个负数减1
• 不能直接用原码计算负数的加减法

于是，反码出现了。

二，反码

1，反码的灵感

反码的灵感来源于数学减法运算的一个定义：和为0的两个数互为相反数。

由这个定义得出一个推论1：假设A/B互为相反数，则A-1的相反数是B+1，那么要求得B+1的值，可以通过先算出A-1的值再取反即可。

基于第一部分发现的规律：对于负数的原码加1，实际上起到了负数减1的效果，那么，结合上面的推论1，有如下假设：

• 我们对负数原码的相反数+1，得到的是比相反数小1的值R
• 对这个值R再取相反数，就相当于得到负数+1的正确结果

形如：


当然，原码的相反数和数学中的相反数不一样，这里的相反数被称为反码。

2，反码的定义

• 反码主要用于在计算机系统中处理负数
• 对于正数，其反码与原码相同
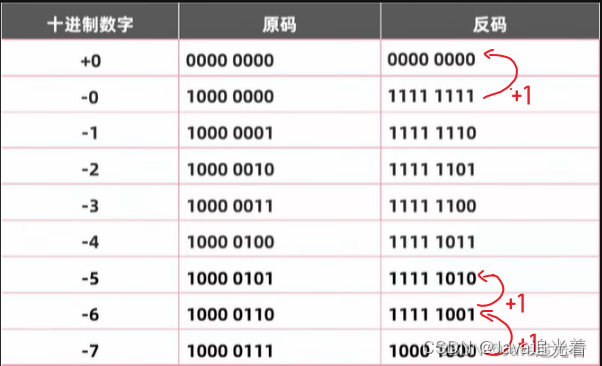
• 对于负数，除了符号位保持不变外，其余各位都要按位取反（0变1，1变0）。比如-5的8位原码是10000101，则反码是11111010

3，反码也搞不定所有负数的加减法

反码的出现，搞定了一部分负数的加减法，有了很大的进步。但是，反码也搞不定所有负数的加减法。

先证明这个结论，请看下面这张表格：

对于反码，从下往上，对每行加1，用反码进行计算，发现：
-7+1 = 1000 1000 + 1 = 1111 1001 = -6 （正确），
-7+1 = 1111 1001 + 1 = 1111 1010 = -5 （正确），
…
-1+1 = 1111 1110 + 1 = 1111 1111 = -0 （正确）

但是，接下来：
-0+1 = 1111 1111 + 1 = 0000 0000 = 0 （错误）

很明显，反码搞不定-0+1 这个表达式。仔细观察上面的表格，错误发生在正负数的边界0处，0非常特殊：

• 0有两个反码，一个正0(0000 0000，正数的反码是原码本身)，一个负0(1111 1111，负数的反码要对原码按位取反)

反码其实已经接近于最终答案了，但是还需优化一下，解决0处的问题。

于是，补码出现了，补码就是就是对反码的优化。

三，补码：现代计算的基础

1，补码的灵感

聪明的计算机科学家发现，反码计算负数的问题主要在于0有两个反码：0000 0000 和 1111 1111，如果对-0的反码1111 1111执行加1的操作，就和+0的反码一致了。

经过验证，这一假设应用到所有的负数的反码上，可以完美的解决负数的计算问题。把负数的反码加1得到的二进制称为补码。

2，什么是补码

• 正数的补码与原码相同
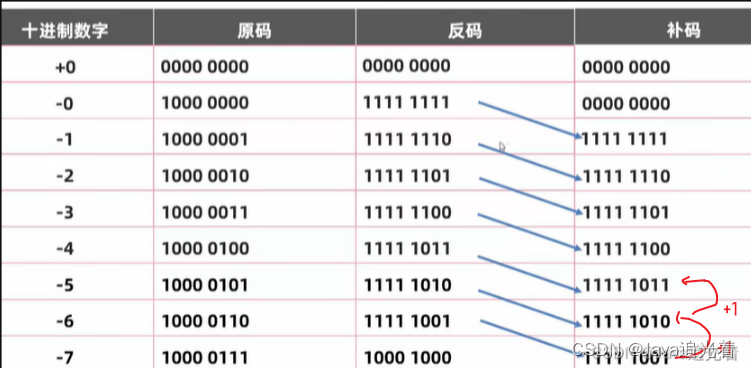
• 负数的补码，则是在其反码的基础上加1。如，-5的8位反码是11111010，则其补码是11111011。

补码的最大好处在于，无论是正数还是负数，加法和减法都可以统一使用加法器完成，简化了硬件设计。

观察上面表格的补码列，再执行从下往上逐行加1的操作，都能得到正确的结果了：

-7+1 = 1111 1001 + 1 = 1111 1010 = -6 （正确），
-7+1 = 1111 1010 + 1 = 1111 1011 = -5 （正确），
…
即使是对于反码不能计算正确的-0+1，用补码计算的结果也是正确的：
-0+1 = 0000 0000 + 1 = 0000 0001 = 1 （正确）

至此，负数的计算得到了完美的解决。

四，总结

1，计算机中的数字是以补码的形式存储的；
2，正数的补码是原码本身；
3，负数的补码等于反码+1；
4，正数的反码也是原码本身；
5，负数的反码通过原码逐位取反；
6，原码是数字的二进制形式。