在三维点云上的应用

PCA 是有损的数据压缩方式，它常用于对高维数据进行降维，也就是把高维数据投影到方差大的几个主方向上，方便数据分析。

让数据集在某个基上的投影值(也是在这个基上的坐标值)越分散，方差越大，这个基保留的信息也就越多
读取点云的代码：

  # 加载原始点云，txt处理
    point_cloud_raw = np.genfromtxt(r"plant_0001.txt", delimiter=",")  #为 xyz的 N*3矩阵
    point_cloud_raw = DataFrame(point_cloud_raw[:, 0:3])  # 选取每一列 的 第0个元素到第二个元素   [0,3)
    point_cloud_raw.columns = ['x', 'y', 'z']  # 给选取到的数据 附上标题
    point_cloud_pynt = PyntCloud(point_cloud_raw)  # 将points的数据 存到结构体中
    point_cloud_o3d = point_cloud_pynt.to_instance("open3d", mesh=False)  # 实例化
    o3d.visualization.draw_geometries([point_cloud_o3d]) # 显示原始点云
    # 从点云中获取点，只对点进行处理
    print(point_cloud_o3d)              #打印点数

主成分方向

# 功能：计算PCA的函数
# 输入：
#     data：点云，NX3的矩阵
#     correlation：区分np的cov和corrcoef，不输入时默认为False  这个没用到
#     sort: 特征值排序，排序是为了其他功能方便使用，不输入时默认为True
# 输出：
#     eigenvalues：特征值
#     eigenvectors：特征向量
def PCA(data, correlation=False, sort=True):
    average_data = np.mean(data,axis=0)       #求 NX3 向量的均值
    decentration_matrix = data - average_data   #去中心化
    H = np.dot(decentration_matrix.T,decentration_matrix)  #求解协方差矩阵 H
    eigenvectors,eigenvalues,eigenvectors_T = np.linalg.svd(H)    # SVD求解特征值、特征向量
    #covX = np.cov(decentration_matrix.T)   #计算协方差矩阵
    #featValue, featVec=  np.linalg.eig(covX)  #求解协方差矩阵的特征值和特征向量

    if sort:
        sort = eigenvalues.argsort()[::-1]      #降序排列
        eigenvalues = eigenvalues[sort]         #索引
        eigenvectors = eigenvectors[:, sort]
       # sort = featValue.argsort()[::-1]      #降序排列
       # featValue = featValue[sort]         #索引
       # featVec = featVec[:, sort]
    return eigenvalues, eigenvectors

 # 用PCA分析点云主方向
    w, v = PCA(point_cloud_raw)        # w为特征值 v为主方向
    point_cloud_vector1 = v[:, 0]   #点云主方向对应的向量，第一主成分
    point_cloud_vector2 = v[:, 1]  # 点云主方向对应的向量，第二主成分
    point_cloud_vector = v[:,0:2]  # 点云主方向与次方向
    print('the main orientation of this pointcloud is: ', point_cloud_vector1)
    print('the main orientation of this pointcloud is: ', point_cloud_vector2)

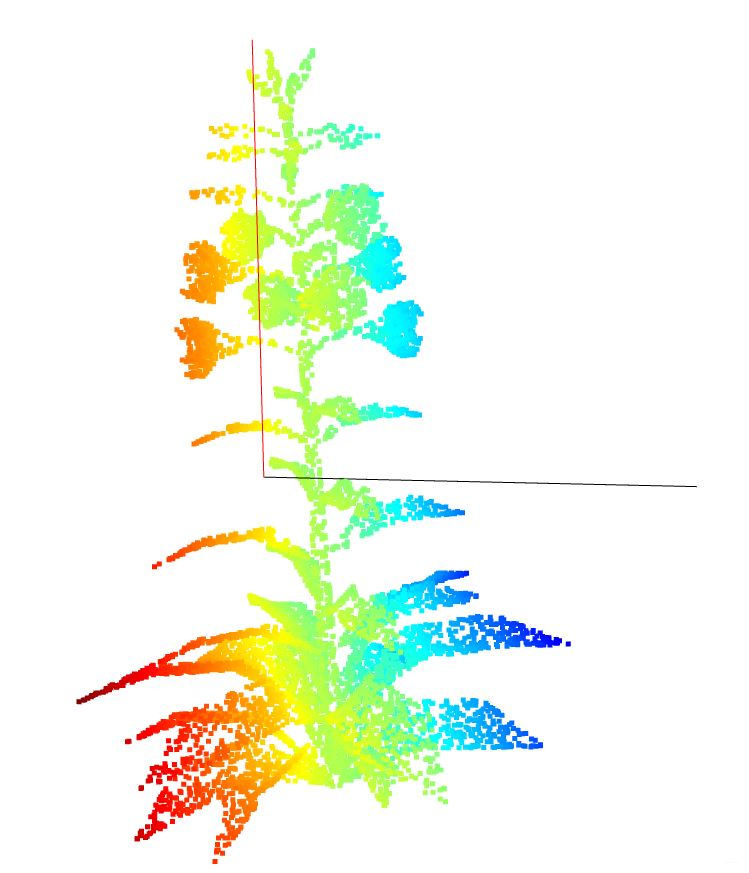
    #在原点云中画图
    point = [[0,0,0],point_cloud_vector1,point_cloud_vector2]  #画点：原点、第一主成分、第二主成分
    lines = [[0,1],[0,2]]      #画出三点之间两两连线
    colors = [[1,0,0],[0,0,0]]
    #构造open3d中的LineSet对象，用于主成分显示
    line_set = o3d.geometry.LineSet(points=o3d.utility.Vector3dVector(point),lines=o3d.utility.Vector2iVector(lines))
    line_set.colors = o3d.utility.Vector3dVector(colors)
    o3d.visualization.draw_geometries([point_cloud_o3d,line_set]) # 显示原始点云和PCA后的连线  

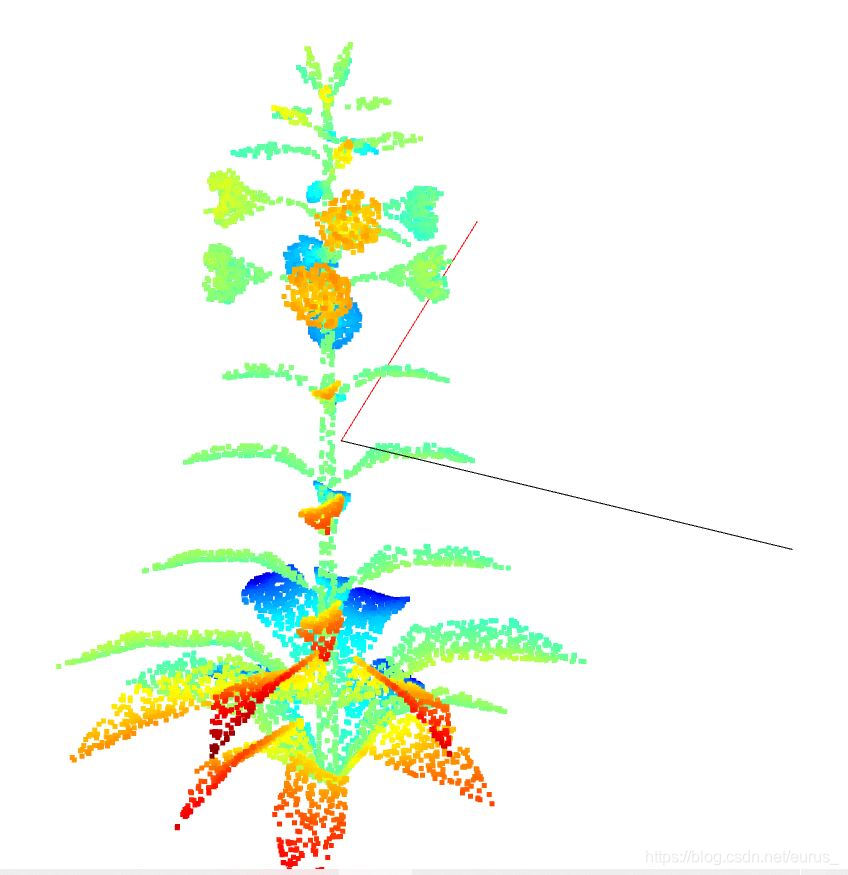
• correlation：区分np的cov和corrcoef，不输入时默认为False
  这个参数是没有用的，尝试过使用corrcoef，结果如下所示，是不对的。分析原因是因为corrcoef计算的是相关系数表示的是单纯反应两个变量每单位变化时的相似程度，会丢失（尺度）信息？所以这个不能来进行计算特征向量，特征值的分解。
  （corrcoef相关系数是用以反映变量之间相关关系密切程度的统计指标。相关系数也可以看成协方差：一种剔除了两个变量量纲影响、标准化后的特殊协方差,它消除了两个变量变化幅度的影响。简单来说，而只是单纯反应两个变量每单位变化时的相似程度。）

• 上面代码中，svd和cov的区别:
  H = np.dot(decentration_matrix.T,decentration_matrix)没有除以样本个数直接计算的是$X{X}^T$而covX = np.cov(decentration_matrix.T)计算的是标准的协方差矩阵$\frac{1}{m}\ast X{X}^T$

以下是三个图的主成分的图示：

SVD主成分分析

COV协方差主成分分析
correlation协方差主成分分析

降维

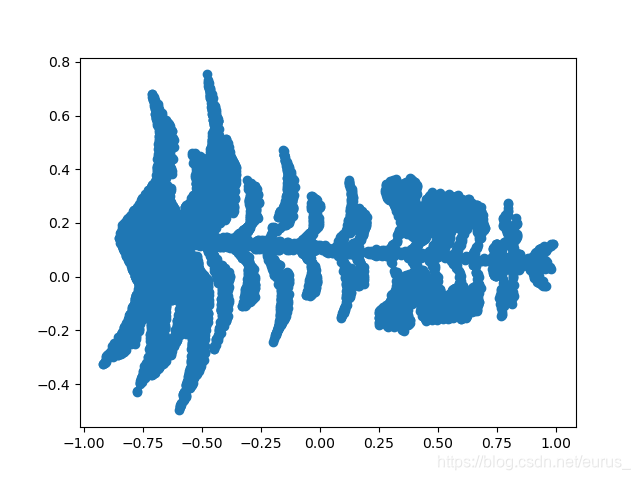
取需要前K个需要降维的特征向量组成降维矩阵；将数据与降维矩阵进行相乘，可让数据降维。

    #将原数据进行降维度处理
    point_cloud_encode = (np.dot(point_cloud_vector.T,point_cloud_raw.T)).T   #主成分的转置 dot 原数据
    Point_Show(point_cloud_encode)
    #使用主方向进行升维
    point_cloud_decode = (np.dot(point_cloud_vector,point_cloud_encode.T)).T
    Point_Cloud_Show(point_cloud_decode)
    point_cloud_raw1=np.asarray(point_cloud_raw)
    Point_Cloud_Show(point_cloud_raw1)
    pcd_raw = o3d.geometry.PointCloud()
    pcd_raw.points = o3d.utility.Vector3dVector(point_cloud_raw1)
    pcd_decode = o3d.geometry.PointCloud()
    pcd_decode.points = o3d.utility.Vector3dVector(point_cloud_decode)
    view_cloud(pcd_raw, pcd_decode)

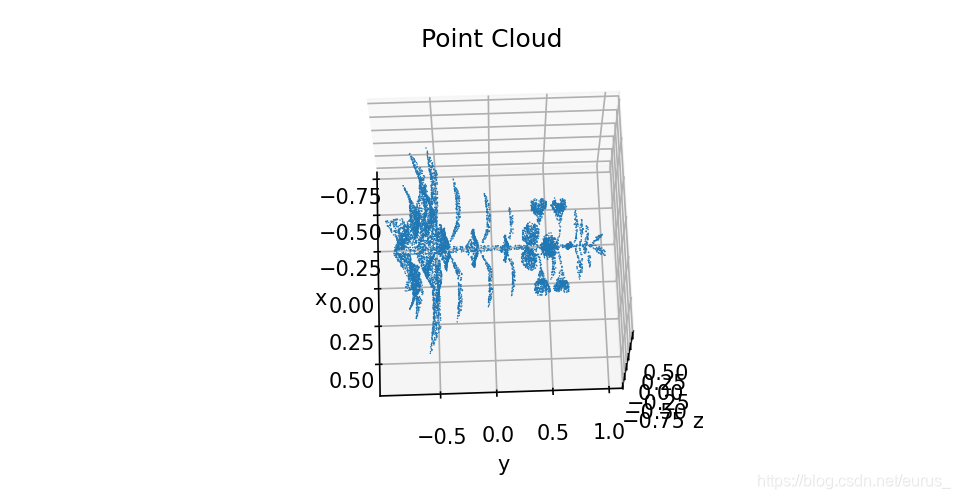
降维后的图片，但是X、Y轴是没有意义的
升维后的点云图
原先点云图

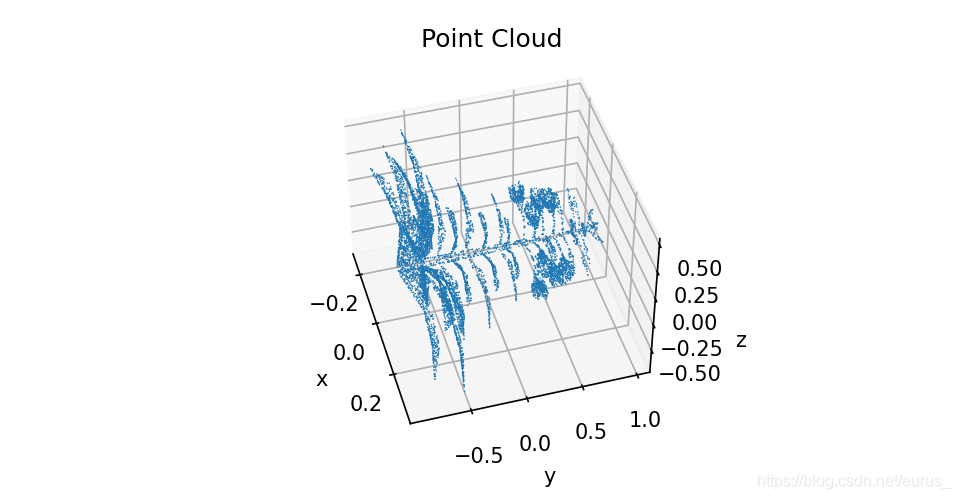
在Open3d中的原先点云图和升维点云图显示：

可以很明显的看出升维后点云缺失了一个厚度的信息，如同薄薄的一张纸片一样，所以这也印证了PCA降维是有损压缩方式

求解点云的法向量

 # 循环计算每个点的法向量
    pcd_tree = o3d.geometry.KDTreeFlann(point_cloud_o3d)           #将原始点云数据输入到KD,进行近邻取点
    normals = []    #储存曲面的法向量
    print(point_cloud_raw.shape[0])      #打印当前点数
    for i in range(point_cloud_raw.shape[0]):
        # search_knn_vector_3d函数 ， 输入值[每一点，x]      返回值 [int, open3d.utility.IntVector, open3d.utility.DoubleVector]
        [_,idx,_] = pcd_tree.search_knn_vector_3d(point_cloud_o3d.points[i],10)      #取10个临近点进行曲线拟合
        # asarray和array 一样 但是array会copy出一个副本，asarray不会，节省内存
        k_nearest_point = np.asarray(point_cloud_o3d.points)[idx, :]  # 找出每一点的10个临近点，类似于拟合成曲面，然后进行PCA找到特征向量最小的值，作为法向量
        w, v = PCA(k_nearest_point)
        normals.append(v[:, 2])#三维点云的第三个特征向量即为其法向量；因为第三个特征向量是最无关的，即为垂直于该平面的法向量

    # 屏蔽结束
    normals = np.array(normals, dtype=np.float64)
    # TODO: 此处把法向量存放在了normals中
    point_cloud_o3d.normals = o3d.utility.Vector3dVector(normals)
    o3d.visualization.draw_geometries([point_cloud_o3d],point_show_normal=True)

结果：

拟合平面

AABB框

点云匹配