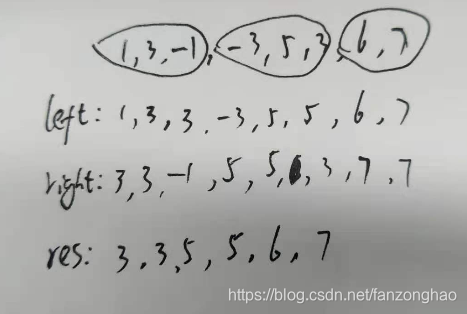思路1:找到状态转移方程:
maxf[i]:表示在i处最大连乘数
minf[i]:表示在i处最小连乘数
maxf[i] = max(nums[i],nums[i]*minf[i-1],nums[i]*maxf[i-1])
minf[i] = min(nums[i],nums[i]*minf[i-1],nums[i]*maxf[i-1])
#maxf[i]:表示在i处最大连乘数
#minf[i]:表示在i处最小连乘数
#maxf[i] = max(nums[i],nums[i]*minf[i-1],nums[i]*maxf[i-1])
#minf[i] = min(nums[i],nums[i]*minf[i-1],nums[i]*maxf[i-1])
class Solution:
def maxProduct(self, nums):
n = len(nums)
maxf,minf = [0]*n,[0] * n
maxf[0],minf[0] = nums[0],nums[0]
for i in range(1,n):
maxf[i] = max(nums[i], nums[i] * minf[i - 1], nums[i] * maxf[i-1])
minf[i] = min(nums[i], nums[i] * minf[i - 1], nums[i] * maxf[i-1])
print('==maxf:', maxf)
return max(maxf)
nums = [2,3,-2,4]
sol = Solution()
sol.maxProduct(nums)思路2:优化版 由于第 i 个状态只和第 i - 1个状态相关,可以只用两个变量来维护 i - 1时刻的状态,一个维护 max, 一个维护 min
class Solution:
def maxProduct(self, nums):
min_value = nums[0]
max_value = nums[0]
res = nums[0]
for i in range(1, len(nums)):
mx = max_value
mn = min_value
max_value = max(nums[i], nums[i]*mx, nums[i]*mn)
min_value = min(nums[i], nums[i]*mx, nums[i]*mn)
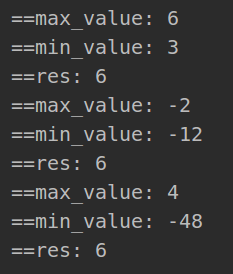
print('==max_value:', max_value)
print('==min_value:', min_value)
res = max(max_value, res)
print('==res:', res)
nums = [2,3,-2,4]
sol = Solution()
sol.maxProduct(nums)50-2.三个数的最大乘积
思路:从小到大排序,如果都是正数则结果是最后三个相乘,如有正有负,结果有可能就是前两个相乘在乘以最后一个正数
class Solution:
def maximumProduct(self, nums):
nums = sorted(nums)
return max(nums[-1]*nums[-2]*nums[-3], nums[0]*nums[1]*nums[-1])
# nums = [1, 2, 3, 4]
nums = [-1, -2, 1, 2, 3]
sol = Solution()
sol.maximumProduct(nums)51. 最小栈
class MinStack:
def __init__(self):
"""
initialize your data structure here.
"""
self.stack = []
def push(self, x: int) -> None:
self.stack.append(x)
def pop(self) -> None:
self.stack.pop()
def top(self) -> int:
return self.stack[-1]
def min(self) -> int:
return min(self.stack)
# Your MinStack object will be instantiated and called as such:
# obj = MinStack()
# obj.push(x)
# obj.pop()
# param_3 = obj.top()
# param_4 = obj.min()c++实现:
class MinStack {
public:
stack<int> stack_A;
stack<int> min_stack;
/** initialize your data structure here. */
MinStack() {
}
void push(int x) {
stack_A.push(x);
if(min_stack.empty() || min_stack.top()>=x){
min_stack.push(x);
}
}
void pop() {
if(stack_A.top() == min_stack.top()){
min_stack.pop();
}
stack_A.pop();
}
int top() {
return stack_A.top();
}
int min() {
return min_stack.top();
}
};
/**
* Your MinStack object will be instantiated and called as such:
* MinStack* obj = new MinStack();
* obj->push(x);
* obj->pop();
* int param_3 = obj->top();
* int param_4 = obj->min();
*/52.多数元素
排序:
class Solution:
def majorityElement(self, nums: List[int]) -> int:
return sorted(nums)[len(nums)//2]投票法(最优解):
class Solution:
def majorityElement(self, nums: List[int]) -> int:
votes = 0
for num in nums:
if votes == 0:
x = num
if num == x:
votes += 1
else:
votes -= 1
# print('==x:', x)
# print('==votes:', votes)
return x53-1.打家劫舍
class Solution(object):
def rob(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
if len(nums)==0:
return 0
if len(nums)<2:
return max(nums)
opt = [0]*len(nums)
opt[0] = nums[0]
opt[1] = max(nums[0],nums[1])
for i in range(2, len(nums)):
opt[i] = max(opt[i-2]+nums[i],opt[i-1])
print('=opt:', opt)
return max(opt)
nums = [2,7,9,3,1]
sol = Solution()
sol.rob(nums)53-2. 打家劫舍 II
class Solution(object):
def rob(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
if len(nums)==0:
return 0
if len(nums)<=2:
return max(nums)
opt1 = [0] * len(nums)
opt2 = [0] * len(nums)
#不抢第一家
opt1[0] = 0
opt1[1] = nums[1]
#不抢最后一家
opt2[0] = nums[0]
opt2[1] = max(nums[:2])
for i in range(2,len(nums)):
opt1[i]=max(opt1[i-2]+nums[i], opt1[i-1])
print(opt1)
for i in range(2, len(nums)-1):
opt2[i] = max(opt2[i - 2] + nums[i], opt2[i - 1])
print(opt2)
return max(opt1[-1],opt2[-2])
nums=[1,2,3,1]
sol = Solution()
res = sol.rob(nums)
print('res:')
print(res)# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def helper(self,node):
if node is None:
return 0, 0
choose_l_value,no_choose_l_value = self.helper(node.left)
choose_r_value,no_choose_r_value = self.helper(node.right)
return node.val+no_choose_l_value+no_choose_r_value, max(choose_l_value,no_choose_l_value)+max(choose_r_value,no_choose_r_value)
def rob(self, root: TreeNode) -> int:
return max(self.helper(root))思路:递归 也就是求1的连通域个数,从1开始进行遍历,将遍历过得1依次置位0,遍历的次数就是连通域个数
# 求1的连通域个数,从1开始进行遍历,将遍历过得1依次置位0,遍历的次数就是连通域个数
class Solution:
def helper(self, i, j, h, w):
if i < 0 or i >= h or j < 0 or j >= w or self.grid[i][j] == "0":
return
self.grid[i][j] = "0"
self.helper(i - 1, j, h, w)
self.helper(i + 1, j, h, w)
self.helper(i, j-1, h, w)
self.helper(i, j+1, h, w)
def numIslands(self, grid):
if len(grid) == 0:
return []
self.grid = grid
h, w = len(grid), len(grid[0])
nums = 0
for i in range(h):
for j in range(w):
if self.grid[i][j] == "1":
nums += 1
self.helper(i, j, h, w)
print('==self.grid:', self.grid)
print('==nums:', nums)
return nums
grid = [
["1", "1", "1", "1", "0"],
["1", "1", "0", "1", "0"],
["1", "1", "0", "0", "0"],
["0", "0", "0", "0", "0"]
]
sol = Solution()
sol.numIslands(grid)
c++实现:
class Solution {
public:
vector<vector<char>> grid;
int h;
int w;
void help(int i, int j){
if(i < 0 || i > this->h - 1 || j < 0 || j > this->w - 1 || this->grid[i][j] == '0'){
return ;
}
this->grid[i][j] = '0';
help(i - 1, j);
help(i + 1, j);
help(i, j - 1);
help(i, j + 1);
}
int numIslands(vector<vector<char>>& grid) {
this->grid = grid;
this->h = grid.size();
this->w = grid[0].size();
int res = 0;
for(int i = 0; i < this->h; i++){
for(int j = 0; j < this->w; j++){
if(this->grid[i][j] == '1'){
res += 1;
}
help(i, j);
}
}
return res;
}
};55.反转链表
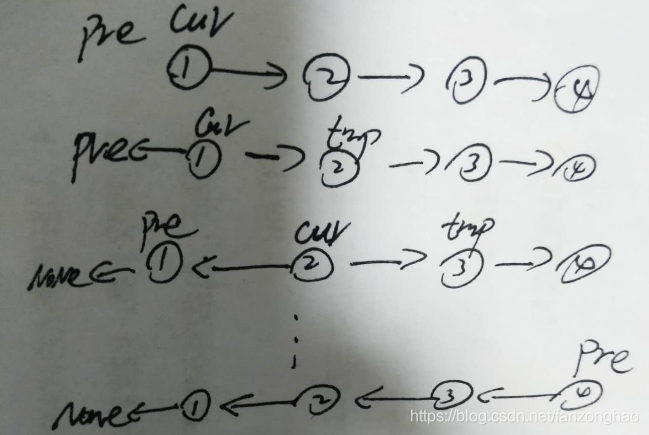
思路1:双指针
class Solution(object):
def reverseList(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
# 申请两个节点,pre和 cur,pre指向None
pre = None
cur = head
# 遍历链表,while循环里面的内容其实可以写成一行
while cur:
# 记录当前节点的下一个节点
tmp = cur.next
# 然后将当前节点指向pre
cur.next = pre
# pre和cur节点都前进一位
pre = cur
cur = tmp
return pre c++实现:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* pre = nullptr;
ListNode* temp = head;
while(head){
temp = head->next;
head->next = pre;
pre = head;
head = temp;
}
return pre;
}
};思路2.递归法
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def reverseList(self, head: ListNode) -> ListNode:
# pre = None
# cur = head
# while cur:
# node = cur.next
# cur.next = pre
# pre = cur
# cur = node
# return pre
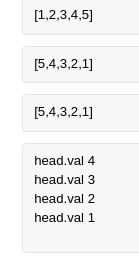
if head is None or head.next is None:
return head
new_node = self.reverseList(head.next)
print('head.val',head.val)
head.next.next = head
head.next = None
return new_node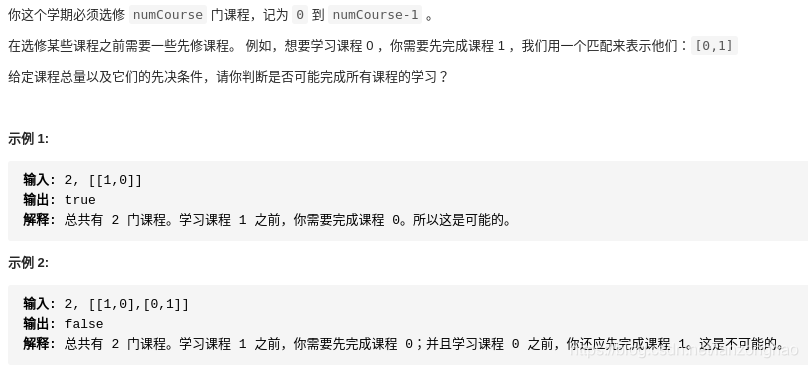
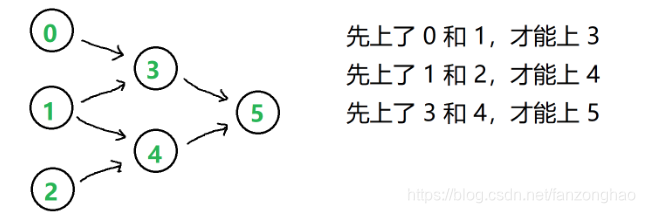
思路:对于这种从图找拓扑排序 ,只有有向无环图能够找到,将入度为0的节点先进入队列,在利用bfs进行出队处理,此时将出队的节点的下一个节点的度进行减一计数,同时遍历的节点数进行加一,最终节点都进行了遍历,则说明找到了拓扑排序.
思路1:用邻接列表
class Solution:
def canFinish(self, numCourses, prerequisites):
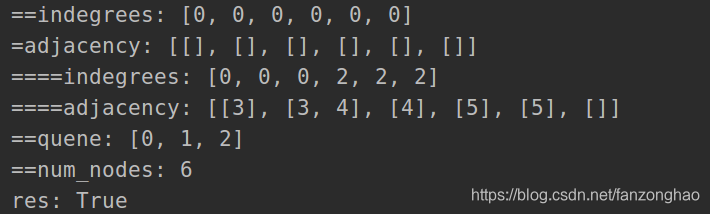
indegrees = [0] * numCourses # 入度列表
print('==indegrees:', indegrees)
adjacency = [[] for i in range(numCourses)] # 邻接列表 存储节点的下一个节点
print('=adjacency:', adjacency)
#得到入度和每个课程的邻接列表
for cur, pre in prerequisites:
indegrees[cur] += 1
adjacency[pre].append(cur)
print('====indegrees:', indegrees)
print('====adjacency:', adjacency)
quene = []
# 如果度为0 就进入队列
for i in range(len(indegrees)):
if indegrees[i] == 0:
quene.append(i)
print('==quene:', quene)
num_nodes = 0
while quene:
node = quene.pop(0)
num_nodes += 1
for next_node in adjacency[node]:
indegrees[next_node] -= 1 # 找出下一个点相应的度-1
if indegrees[next_node] == 0: # 入度为0
quene.append(next_node)
print('==num_nodes:', num_nodes)
return num_nodes == numCourses
# numCourses, prerequisites = 2, [[1, 0]]
# numCourses, prerequisites = 2, [[1, 0], [0, 1]]
numCourses, prerequisites = 6, [[3, 0], [3, 1], [4, 1], [4, 2], [5, 3], [5, 4]]
sol = Solution()
res = sol.canFinish(numCourses, prerequisites)
print('res:', res)思路2:用邻接矩阵的bfs
class Solution:
def canFinish(self, numCourses, prerequisites):
indegrees = [0] * numCourses # 度列表
adjacency = [[0 for i in range(numCourses)] for i in range(numCourses)] # 邻接矩阵 表示节点之间关系
print('==init adjacency:', adjacency)
for cur, pre in prerequisites:
indegrees[cur] += 1
adjacency[pre][cur] = 1
print('==init adjacency complete:', adjacency)
print('==init indegrees complete:', indegrees)
quene = []
for i in range(len(indegrees)):
if indegrees[i] == 0:
quene.append(i)
print('==quene:', quene)
num_nodes = 0
while quene:
node = quene.pop()
num_nodes += 1
for j in range(numCourses):
if adjacency[node][j] == 1:
next_node = j
adjacency[node][j] -= 1
indegrees[next_node] -= 1
if indegrees[next_node] == 0:
quene.append(next_node)
print('==num_nodes:', num_nodes)
return num_nodes == numCourses
# numCourses = 2
# prerequisites = [[0, 1]]
numCourses = 4
prerequisites = [[1, 0], [2, 0], [3,1],[3,2]]
sol = Solution()
sol.canFinish(numCourses, prerequisites)思路:有向无环图,BFS遍历
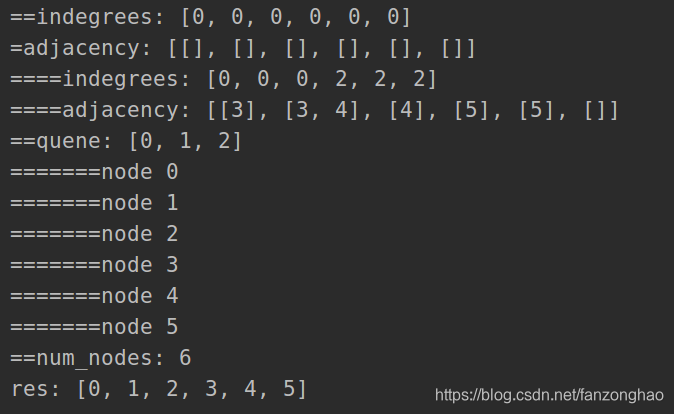
class Solution:
def canFinish(self, numCourses, prerequisites):
indegrees = [0] * numCourses # 入度列表
print('==indegrees:', indegrees)
adjacency = [[] for i in range(numCourses)] # 邻接列表
print('=adjacency:', adjacency)
#得到入度和每个课程的邻接列表
for cur, pre in prerequisites:
indegrees[cur] += 1
adjacency[pre].append(cur)
print('====indegrees:', indegrees)
print('====adjacency:', adjacency)
quene = []
# 如果度为0 就进入队列
for i in range(len(indegrees)):
if indegrees[i] == 0:
quene.append(i)
print('==quene:', quene)
num_nodes = 0
learn_node = []
while quene:
node = quene.pop(0)
print('=======node', node)
learn_node.append(node)
num_nodes += 1
for next_node in adjacency[node]:
indegrees[next_node] -= 1 # 找出下一个点相应的度-1
if indegrees[next_node] == 0: # 入度为0
quene.append(next_node)
print('==num_nodes:', num_nodes)
return learn_node if num_nodes == numCourses else []
# numCourses, prerequisites = 2, [[1, 0]]
# numCourses, prerequisites = 2, [[1, 0], [0, 1]]
numCourses, prerequisites = 6, [[3, 0], [3, 1], [4, 1], [4, 2], [5, 3], [5, 4]]
sol = Solution()
res = sol.canFinish(numCourses, prerequisites)
print('res:', res)思路2:用邻接矩阵的bfs
class Solution:
def canFinish(self, numCourses, prerequisites):
indegrees = [0] * numCourses # 度列表
adjacency = [[0 for i in range(numCourses)] for i in range(numCourses)] # 邻接矩阵 表示节点之间关系
print('==init adjacency:', adjacency)
for cur, pre in prerequisites:
indegrees[cur] += 1
adjacency[pre][cur] = 1
print('==init adjacency complete:', adjacency)
print('==init indegrees complete:', indegrees)
quene = []
for i in range(len(indegrees)):
if indegrees[i] == 0:
quene.append(i)
print('==quene:', quene)
num_nodes = 0
learn_nodes = []
while quene:
node = quene.pop()
learn_nodes.append(node)
num_nodes += 1
for j in range(numCourses):
if adjacency[node][j] == 1:
next_node = j
adjacency[node][j] -= 1
indegrees[next_node] -= 1
if indegrees[next_node] == 0:
quene.append(next_node)
print('==num_nodes:', num_nodes)
print('=learn_nodes:', learn_nodes)
return learn_nodes if num_nodes == numCourses else []
# numCourses = 2
# prerequisites = [[0, 1]]
numCourses = 4
prerequisites = [[1, 0], [2, 0], [3,1],[3,2]]
sol = Solution()
sol.canFinish(numCourses, prerequisites)
思路:利用字典存储每个单词,同时用特殊字符结尾。
class Trie:
def __init__(self):
"""
Initialize your data structure here.
"""
self.root = {}
self.word_end = -1
def insert(self, word):
"""
Inserts a word into the trie.
"""
curNode = self.root
for c in word:
if c not in curNode:
curNode[c] = {}
curNode = curNode[c]
curNode[self.word_end] = True
# print('==curNode:', curNode)
def search(self, word):
"""
Retu
rns if the word is in the trie.
"""
curNode = self.root
for c in word:
if c not in curNode:
return False
curNode = curNode[c]
if self.word_end not in curNode:
return False
return True
def startsWith(self, prefix):
"""
Returns if there is any word in the trie that starts with the given prefix.
"""
curNode = self.root
for c in prefix:
if c not in curNode:
return False
curNode = curNode[c]
return True
word = 'apple'
prefix = 'ad'
obj = Trie()
obj.insert(word='apple')
obj.insert(word='add')
# obj.insert(word='app')
print('tree:', obj.root)
param_2 = obj.search(word)
print('search res:', param_2)
param_3 = obj.startsWith(prefix)
print('==param_3:', param_3)思路:排序 取第k个值就可
class Solution:
def quicksort(self, arr):
if len(arr) <= 1:
return arr
privot = arr[len(arr) // 2]
left = [i for i in arr if i < privot]
middle = [i for i in arr if i == privot]
right = [i for i in arr if i > privot]
# left = [arr[i] for i in range(len(arr)) if arr[i] < privot]
# middle = [arr[i] for i in range(len(arr)) if arr[i] == privot]
# right = [arr[i] for i in range(len(arr)) if arr[i] > privot]
return self.quicksort(left) + middle + self.quicksort(right)
def findKthLargest(self, nums, k):
return self.quicksort(nums)[::-1][k-1]
# nums = [3, 2, 1, 5, 6, 4]
# k = 2
nums = [3,2,3,1,2,4,5,5,6]
k = 4
sol = Solution()
res = sol.findKthLargest(nums, k)
print('res:', res)思路2:topk问题用最小堆
class Solution:
def findKthLargest(self, nums, k):
arr = []
heapq.heapify(arr)
for i in range(k):
heapq.heappush(arr, nums[i])
for i in range(k, len(nums)):
heapq.heappush(arr, nums[i])
heapq.heappop(arr)
print('==arr:', arr)
return arr[0]
arr = [3,2,1,5,6,4]
k = 2
sol = Solution()
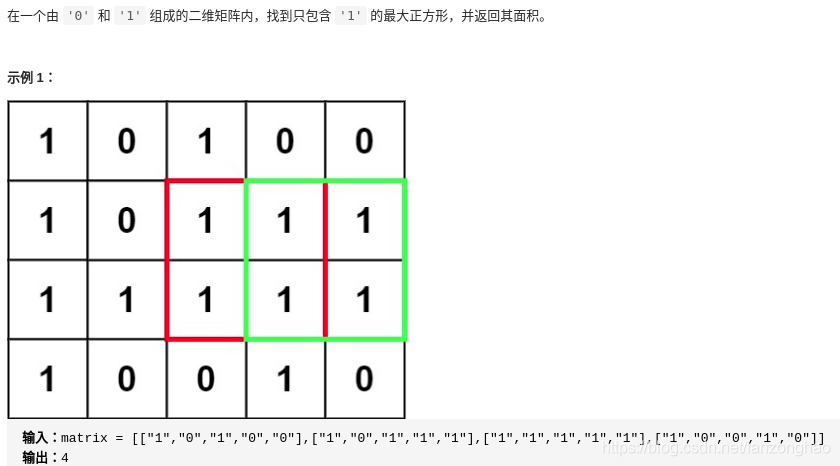
sol.findKthLargest(arr, k)思路:题目既然求最大正方形面积,那就先由2*2正方形拓展更大即可,也就是可以用动态规划来存储左上角,左边,上边的最小值,也是正方形边长
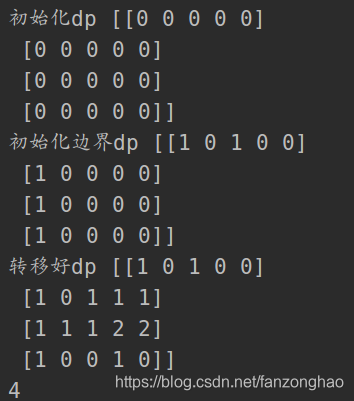
1.转移方程为 dp[i][j] = min(dp[i-1][j],dp[i][j-1].dp[i-1][j-1])+1
2.初始化边界条件为: dp[:][0] = matrix[:][0] dp[0][:] = matrix[0][:]
class Solution:
def maximalSquare(self, matrix):
max_side = 0
h,w = len(matrix),len(matrix[0])
dp = [[0 for i in range(w)] for i in range(h)]
print('初始化dp',np.array(dp))
for i in range(h):
dp[i][0] = int(matrix[i][0])
max_side = max(max_side, dp[i][0])
for i in range(w):
dp[0][i] = int(matrix[0][i])
max_side = max(max_side, dp[0][i])
print('初始化边界dp',np.array(dp))
for i in range(1,h):
for j in range(1,w):
if matrix[i][j]=='1':
dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1])+1
max_side = max(max_side, dp[i][j])
print('转移好dp',np.array(dp))
return max_side**2
matrix = [["1","0","1","0","0"],
["1","0","1","1","1"],
["1","1","1","1","1"],
["1","0","0","1","0"]]
# matrix = [["0","1"],["1","0"]]
sol = Solution()
res= sol.maximalSquare(matrix)
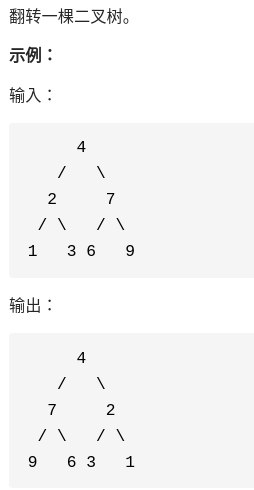
print(res)60.翻转二叉树
思路:递归遍历左右子树进行交换即可
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def invertTree(self, root: TreeNode) -> TreeNode:
if root is None:
return None
left = self.invertTree(root.left)
right = self.invertTree(root.right)
root.left = right
root.right = left
return rootc++实现:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if(root == nullptr){
return nullptr;
}
TreeNode* left = invertTree(root->left);
TreeNode* right = invertTree(root->right);
root->left = right;
root->right = left;
return root;
}
};利用列表将列表值进行拷贝,在判断是否是回文字符串
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def isPalindrome(self, head: ListNode) -> bool:
stack= []
while head:
stack.append(head.val)
head = head.next
return stack==stack[::-1]c++实现:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
bool isPalindrome(ListNode* head) {
vector<int> res;
while(head){
res.push_back(head->val);
head = head->next;
}
int left=0;
int right=res.size()-1;
while(left<right){
if(res[left]==res[right]){
left+=1;
right-=1;
}
else{
return false;
}
}
return true;
}
};# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
if root is None or root==p or root==q:#递归终止条件 节点为空 或者节点等于p,q其中之一
return root
left = self.lowestCommonAncestor(root.left, p, q)#遍历左子树
right = self.lowestCommonAncestor(root.right, p, q)#遍历右子树
if left is None:#左子树为空 就去右子树
return right
if right is None:#右子树为空 就去左子树
return left
return root#左右子树都不为空 说明找到了节点 c++实现:
代码段 小部件
63.除自身以外数组的乘积
思路1:超时
#超时时间复杂度O(N)
class Solution:
def productExceptSelf(self, nums):
output = len(nums)*[0]
for i in range(len(nums)):
temp = 1
for j in nums[:i]:
temp*=j
for j in nums[i+1:]:
temp*=j
output[i] = temp
# print('==output:', output)
return output
nums = [1, 2, 3, 4]
sol = Solution()
sol.productExceptSelf(nums)思路2:利用空间换时间
1.借用左右数组来存储值,L[i]代表i左边的乘积值,R[i]代表i右边的乘积值
2.最终i处的值为L[i]*R[i]
class Solution:
def productExceptSelf(self, nums):
length = len(nums)
L,R,output = [0]*length,[0]*length,[0]*length
L[0] = 1
for i in range(1, length):
L[i] = L[i-1]*nums[i-1]
print('==L:', L)
R[length-1] = 1
for i in range(length-2, -1, -1):
print('==i:', i)
R[i] = R[i + 1] * nums[i + 1]
print('==R:', R)
for i in range(length):
output[i] = L[i]*R[i]
return output
nums = [1, 2, 3, 4]
sol = Solution()
sol.productExceptSelf(nums)思路1.超时O(n*k)
class Solution:
def maxSlidingWindow(self, nums, k):
#时间复杂度O(Nk)超时了
res = []
for i in range(len(nums)-k+1):
res.append(max(nums[i:i+k]))
return res思路2:
动态规划:时间复杂度O(N)
1.将数组分成k+1个,剩下的一个可能不足;
2.left数组存储每个拆分的从左到右的值,对于left来说每个块最右边元素最大;
3.right数组存储每个拆分的从右到左的值,对于right来说每个块最左边元素最大;
4.最后在利用left和right求最大值,max(left[i],right(j)) i每个块最右边元素索引,j每个块最左边元素索引
class Solution:
def maxSlidingWindow(self, nums, k):
n = len(nums)
if n * k == 0:
return []
if k == 1:
return nums
left = [0] * n
left[0] = nums[0]
right = [0] * n
right[n - 1] = nums[n - 1]
for i in range(1, n):
#从左往右
if i%k==0:#分块的第一个元素
left[i] = nums[i]
else:
left[i] = max(left[i-1],nums[i])
# 从右往左
j = n-i-1
# 分块的最右边元素
if (j+1) % k == 0:
right[j] = nums[j]
else:
right[j] = max(right[j + 1], nums[j])
print('===left:', left)
print('===right:', right)
#最后在利用left和right求最大值
output = []
for i in range(n - k + 1):
output.append(max(left[i + k - 1], right[i]))
return output
nums = [1,3,-1,-3,5,3,6,7]
k = 3
sol = Solution()
res = sol.maxSlidingWindow(nums, k)
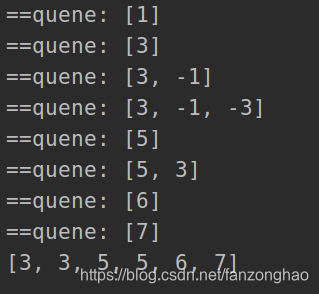
print('res:', res)思路3:双端队列:用一个队列一直存储更新最大值
# 双端队列:用一个队列一直存储更新最大值
class Solution:
def maxSlidingWindow(self, nums, k):
length = len(nums)
if length == 0:
return []
res = []
quene = []
for j in range(length):
i = j-k+1
if i > 0 and quene[0] == nums[i-1]:#当要左移掉的元素等于quene头部元素,那么quene就移除头部元素
quene.pop(0)
while quene and quene[-1] < nums[j]:#保持quene里面都是单调递减的,且头部元素最大
quene.pop()
quene.append(nums[j])
print('==quene:', quene)
if i >= 0:
res.append(quene[0])
return res
nums = [1, 3, -1, -3, 5, 3, 6, 7]
k = 3
sol = Solution()
res = sol.maxSlidingWindow(nums, k)
print(res)c++代码:
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
vector<int> res;
deque<int> queue_A;
for(int i=0;i<nums.size();i++){
int j=i-k+1;
if(j>0 && nums[j-1]==queue_A.front()){
queue_A.pop_front();
}
while (queue_A.size() && queue_A.back()<nums[i])
{
queue_A.pop_back();
}
queue_A.push_back(nums[i]);
if(j>=0){
res.push_back(queue_A.front());
}
}
return res;
}
};class Solution:
def find(self,number,matrix):
rows=len(matrix)#行数
cols=len(matrix[0])#列数
if rows<0 and cols<0:
return False
col=0
row=rows-1
while row>=0 and col<cols:
if matrix[row][col]<number:
col+=1
elif matrix[row][col]>number:
row-=1
else:
return True#找到
return False#没找到
if __name__ == '__main__':
matrix = [[1, 3, 5, 6],
[2, 5, 8, 12],
[4, 9, 10, 17],
[6, 11, 11, 18]]
sol=Solution()
print(sol.find(17,matrix))
思路:可看成M(n) = M(n-1k)+1,这里就可以用回溯当成求子集问题,但是容易超出时间限制.
1.回溯
#公式为 M(n) = M(n - k) + 1
import math
class Solution(object):
def numSquares(self, n):
square_nums = [i**2 for i in range(1, int(math.sqrt(n))+1)]
print('==square_nums:', square_nums)
res = []
track = []
def minNumSquares(k,track):
""" recursive solution """
# bottom cases: find a square number
if k in square_nums:
track.append(k)
res.append(track)#满足选择条件
return 1
min_num = float('inf')
# Find the minimal value among all possible solutions
for square in square_nums:
if k < square:
break
# 满足选择列表
store = track.copy()
track.append(square)#做选择
new_num = minNumSquares(k-square, track) + 1#回溯
track = store#撤消选择
min_num = min(min_num, new_num)
return min_num
return minNumSquares(n, track), res
n = 3
sol = Solution()
numbers, res = sol.numSquares(n)
print('个数:', numbers, res)
2.对于递归这种,其实都是可以用dp来减少计算量
#公式为 M(n) = M(n - k) + 1
class Solution(object):
def numSquares(self, n):
"""
:type n: int
:rtype: int
"""
square_nums = [i ** 2 for i in range(0, int(math.sqrt(n)) + 1)]
print('square_nums==:', square_nums)
dp = [float('inf')] * (n + 1)
# bottom case
dp[0] = 0
for i in range(1, n + 1):
for square in square_nums:
if i < square:#小于平方的数 就break
break
print('==square:', square)
dp[i] = min(dp[i], dp[i - square] + 1)
print('==dp:', dp)
return dp[-1]
n = 4
sol = Solution()
numbers = sol.numSquares(n)
print('个数:', numbers)c++实现:
class Solution {
public:
int numSquares(int n) {
vector<int> dp(n+1, INT_MAX);
vector<int> nums;
for(int i=1; i < int(sqrt(n)) + 1; i++){
nums.push_back(pow(i, 2));
}
dp[0] = 0;
for(int i = 1; i < n+1; i++){
for(int j=0; j < nums.size(); j++){
if(i < nums[j]){
break;
}
dp[i] = min(dp[i], dp[i - nums[j]] + 1);
}
}
return dp[n];
}
};67.移动零
思路1:移0法
class Solution:
def moveZeroes(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
n = len(nums)
i=0
while 0 in nums:
nums.remove(0)
i+=1
nums.extend([0]*i)
return nums
思路2:指针记录非0索引
class Solution:
def moveZeroes(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
idx = 0
n = len(nums)
for i in range(len(nums)):
if nums[i]!=0:
nums[idx] = nums[i]
idx+=1
nums[idx:] = (n - idx )*[0]
return nums思路3:指针 交换数字
class Solution:
def moveZeroes(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
idx = 0
n = len(nums)
for i in range(len(nums)):
if nums[i]!=0:
nums[idx], nums[i] = nums[i], nums[idx]
idx+=1
# print(idx)
# print(nums)
# nums[idx:] = (n - idx )*[0]
return nums
思路4:优化特殊非0元素
class Solution:
def moveZeroes(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
idx = 0
n = len(nums)
for i in range(len(nums)):
if nums[i]!=0:
if i!=idx:
nums[idx], nums[i] = nums[i], nums[idx]
idx+=1
else:
idx +=1
# print(idx)
# print(nums)
# nums[idx:] = (n - idx )*[0]
return nums
68.寻找重复数
思路:对于上述题目示例1,将数组值作为索引,会发现陷入无穷循环,而无穷循环的起始点就是重复出现的数,故构成一个环,所以就想到用快慢指针进行解决,如下图所示,A是起点,B是环开始点,C是相遇点,快指针是慢指针速度的两倍。
在C点相遇以后,在从起始点和C点用相同速度奔跑,就在B点相遇了,即可以得到重复的数字。
class Solution:
def findDuplicate(self, nums: List[int]) -> int:
fast = 0
slow = 0
while True:
# print('==fast:', fast)
# print('==slow:', slow)
fast = nums[nums[fast]]
slow = nums[slow]
if fast == slow:
break
start = 0
while True:
start = nums[start]
fast = nums[fast]
if start ==fast:
break
# print(start)
return start思路:利用dp,一个数组存储向上递增的长度,一个数组存储相同长度序列的个数
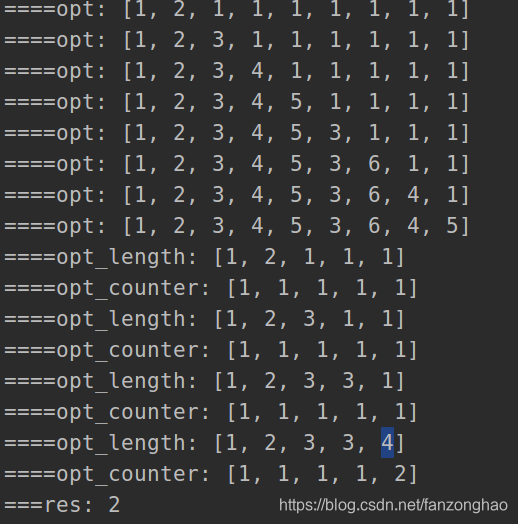
class Solution:
def findNumberOfLIS(self, nums):
if nums ==[]:
return(0)
n = len(nums)
opt_length = [1]*n
opt_counter = [1]*n
for i in range(1, n):
for j in range(i):
if nums[j] < nums[i]:
if opt_length[j]+1 > opt_length[i]:# 代表第一次遇到最长子序列
opt_length[i] = 1+opt_length[j]
opt_counter[i] = opt_counter[j]
elif opt_length[j]+1 == opt_length[i]:# 代表已经遇到过最长子序列
opt_counter[i] = opt_counter[i]+opt_counter[j]
# print('====opt_length:', opt_length)
# print('====opt_counter:', opt_counter)
tmp = max(opt_length)
res = sum([opt_counter[i] for i in range(n) if opt_length[i] == tmp])
return (res)
sol = Solution()
nums = [1, 3, 5, 4, 7]
res = sol.findNumberOfLIS(nums)
print('===res:', res)思路:回溯
class Solution:
def removeInvalidParentheses(self, s: str) -> List[str]:
if not s:
return [""]
if s[0] not in "()":
return [s[0]+i for i in self.removeInvalidParentheses(s[1:])]
if len(s) < 2:
return [""]
if s[0] == ")":
return self.removeInvalidParentheses(s[1:])
res = set(self.removeInvalidParentheses(s[1:]))
for i in range(1, len(s)):
if s[i] == ")":
a, b = set(self.removeInvalidParentheses(s[1:i])), set(self.removeInvalidParentheses(s[i+1:]))
res |= {f"({i}){j}" for i in a for j in b}
p = len(max(res, key=len))
return [i for i in res if len(i) == p]思路:找准状态状转移方程,f代表选择银币的函数,则f(11)=f(11-1)+1或f(11)=f(11-2)+1或f(11)=f(11-5)+1,则一般方程为:
f(money) = min(f(money), f(money-coin)+1)
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
#状态转移方程f(money) = min(f(money),f(money-coin)+1)
f = [float('inf')] * (amount + 1)
f[0] = 0
# print('==f:', f)
for i in range(1, amount + 1):
for coin in coins:
if i - coin >= 0:
f[i] = min(f[i], f[i - coin] + 1)
# print('==f:', f)
return f[-1] if f[-1]!=float('inf') else -1
思路1:回溯 会超时
# 组合问题 回溯 超时
class Solution:
def backtrace(self, amount, start, coins, track):
if amount == 0: # 终止条件
# self.res.append(track)
self.res+=1
return
for i in range(start, len(coins)): # 选择条件
if coins[i] > amount:
continue
# store = track.copy()
# track.append(coins[i])
self.backtrace(amount - coins[i], i, coins, track)
# track = store
def change(self, amount, coins):
self.res = 0#[]
coins = sorted(coins)
self.backtrace(amount, 0, coins, [])
return self.res
# amount = 5
# coins = [2]
amount = 5
coins = [1, 2, 5]
# amount = 500
# coins = [3,5,7,8,9,10,11]
sol = Solution()
res = sol.change(amount, coins)
print('==res:', res)
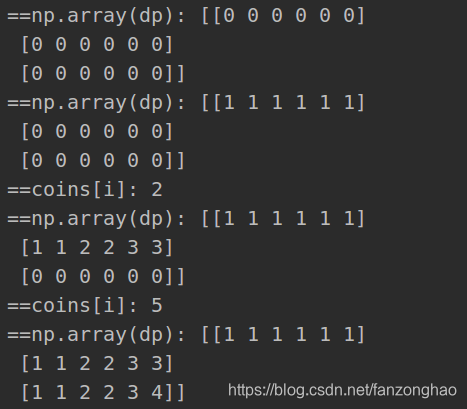
思路2:当成完全背包问题,用dp
#dp[i][j] 硬币为i 金额为j的组合数
import numpy as np
class Solution:
def change(self, amount, coins):
if len(coins) == 0:
if amount == 0:
return 1
else:
return 0
dp = [[0 for i in range(amount+1)] for j in range(len(coins))]
print('==np.array(dp):', np.array(dp))
dp[0][0] = 1
for j in range(coins[0], amount+1, coins[0]):
dp[0][j] = 1
print('==np.array(dp):', np.array(dp))
for i in range(1, len(coins)):
print('==coins[i]:', coins[i])
for j in range(amount+1):
dp[i][j] = dp[i - 1][j]#不选
if j >= coins[i]:#选 注意与0 1背包有一点不同
dp[i][j] += dp[i][j - coins[i]]
print('==np.array(dp):', np.array(dp))
return dp[-1][-1]
amount = 5
coins = [1, 2, 5]
sol = Solution()
sol.change(amount, coins)
思路:
#思路:计算n的时候n-1计算过了
#n&n-1 就是抹掉二进制n最右边的1
class Solution:
def countBits(self, num):
#动态规划
res = [0]*(num+1)
for i in range(1, num+1):
res[i] = res[i & i-1] + 1
return res
num = 5
sol = Solution()
res = sol.countBits(num)
print('==res:', res)思路:hash字典
class Solution:
def topKFrequent(self, nums, k):
dict_ = {}
for num in nums:
dict_[num] = dict_.get(num, 0)+1
print('==dict_:', dict_)
sort_dict = sorted(dict_.items(), key=lambda x:(x[-1], x[0]), reverse=True)
return [sort_dict[j][0] for j in range(k)]
# nums = [1,1,1,2,2,3]
# k = 2
nums = [-1, -1]
k = 1
# nums = [1, 2]
# k = 2
sol = Solution()
res = sol.topKFrequent(nums, k)
print('==res:', res)74.字符串解码
思路:栈
class Solution:
def decodeString(self, s):
stack = [] # (str, int) 记录之前的字符串和括号外的上一个数字
num = 0
res = "" # 实时记录当前可以提取出来的字符串
for c in s:
if c.isdigit():
num = num * 10 + int(c)
elif c == "[":
stack.append((res, num))
res, num = "", 0
elif c == "]":
top = stack.pop()
print('===top:', top)
res = top[0] + res * top[1]
print('==res:', res)
else:
res += c
return res
# s = "3[a]2[bc]"
s = "3[a2[c]]"
sol = Solution()
res = sol.decodeString(s)
print('res:', res)思路:并查集
# 并查集
class Solution:
def __init__(self):
self.f = {} # 每个节点的依次关系
self.d = {} # 每个节点的值 将根节点值置为1
def find(self, x): # 查找与你连通的最上面一位
self.f.setdefault(x, x)
self.d.setdefault(x, 1)
if self.f[x] == x:
return x
else:
t = self.f[x]
self.f[x] = self.find(t)
self.d[x] *= self.d[t]
return self.f[x]
def union(self, A, B, value): # 合并集
a, b = self.find(A), self.find(B)
if a != b:
self.f[a] = b
self.d[a] = self.d[B] / self.d[A] * value
# print('===f===:', f)
# print('===d===:', d)
def check(self, x, y):
if x not in self.f or y not in self.f:
return -1.0
a, b = self.find(x), self.find(y)
# print('==a, b:', a, b)
if a != b: # 如果不在同一条线上就返回-1
return -1.0
return self.d[x] / self.d[y]
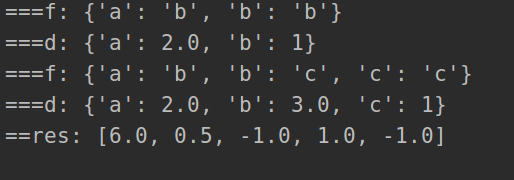
def calcEquation(self, equations, values, queries):
for i, nums in enumerate(equations):
self.union(nums[0], nums[1], values[i])
print('===f:', self.f)
print('===d:', self.d)
res = []
for x, y in queries:
res.append(self.check(x, y))
return res
equations = [["a", "b"], ["b", "c"]]
values = [2.0, 3.0]
queries = [["a", "c"], ["b", "a"], ["a", "e"], ["a", "a"], ["x", "x"]]
# equations = [["a","b"]]
# values = [2.0]
# queries = [["a","c"],["b","a"],["a","e"],["a","a"],["x","x"]]
sol = Solution()
res = sol.calcEquation(equations, values, queries)
print('==res:', res)思路:按身高由高到低进行排序,身高相等时按索引从小排序
#新建一个队列按照索引进行插入
#思路:按身高由高到低进行排序,身高相等时按索引从小排序
#新建一个队列按照索引进行插入
class Solution:
def reconstructQueue(self, people):
people = sorted(people, key=lambda x: (-x[0], x[1]))
print('===people:', people)
output = []
for p in people:
print('===p:', p)
output.insert(p[1], p)
print('==output:', output)
return output
people = [[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]]
sol = Solution()
sol.reconstructQueue(people)77-1.目标和
思路2:动态规划 dp[i][j]表示到i为止,数字和为j的方案数,下面以两个例子为例
# dp[i][j] = dp[i-1][j-nums[i]]+dp[i-1][j+nums[i]]
class Solution:
def findTargetSumWays(self, nums, S):
sum_ = sum(nums)
if abs(S) > sum_:
return 0
opt = [[0 for i in range(2 * sum_ + 1)] for i in range(len(nums))]
print(np.array(opt))
##nums = [0,0,0,0,0,0,0,0,1]
# S = 1
if nums[0] == 0: # 边界条件
opt[0][sum_] = 2
else:
opt[0][sum_ - nums[0]] = 1
opt[0][sum_ + nums[0]] = 1
print(np.array(opt))
for i in range(1, len(nums)):
for j in range(2 * sum_ + 1):
l = j - nums[i] if j - nums[i] > 0 else 0
r = j + nums[i] if j + nums[i] < 2 * sum_ + 1 else 0
opt[i][j] = opt[i - 1][l] + opt[i - 1][r]
# print('===print(np.array(opt)):', np.array(opt))
return opt[-1][sum_ + S]
# nums = [1, 1, 1, 1, 1]
# S = 3
# nums = [1000]
# S = 1000
nums = [0, 0, 0, 0, 0, 0, 0, 0, 1]
S = 1
sol = Solution()
res = sol.findTargetSumWays(nums, S)
print('==res:', res)思路1:
(1)转换成0 1背包问题,找到数组和的一半的子集
(2)dp[i][j]表示到i为止和为j是否存在
(3)dp[i][j] = dp[i-1][j] 不选择nums[i]
(4)dp[i][j] = dp[i-1][j-nums] 选择nums[i]
(5)如果 j<nums[i] dp[i][j] = dp[i-1][j]
以[1,2,3,6]为例
#转换成0 1背包问题 找到数组和的一半的子集
#到i为止和为j是否存在
#dp[i][j] = dp[i-1][j]#不选择nums[i]
#dp[i][j] = dp[i-1][j-nums]#选择nums[i]
#如果 j<nums[i] dp[i][j] = dp[i-1][j]
class Solution:
def canPartition(self, nums):
# nums = sorted(nums)
# print('==nums:', nums)
n = len(nums)
if n<2:#数组长度无法划分
return False
sum_ = sum(nums)
max_value = max(nums)
if sum_ % 2==1:#奇数的话没法拆分
return False
target = sum_//2
if max_value>target:#最大值大于一半了 不满足条件
return False
dp = [[False for i in range(target+1)] for i in range(n)]
print('===np.array(dp):', np.array(dp))
for i in range(n):#不选取任何正整数,则被选取的正整数等于 00
dp[i][0] = True
dp[0][nums[0]] = True#i==0 只有一个正整数 nums[0] 可以被选取
for i in range(1,n):
for j in range(1, target+1):
if j<nums[i]:#j<nums[i]
dp[i][j] = dp[i-1][j]
else:#不选择nums[i]与选择nums[i]
dp[i][j] = dp[i - 1][j] or dp[i - 1][j-nums[i]]
print('===np.array(dp):', np.array(dp))
return dp[-1][target]
# nums = [1, 5, 11, 5]
nums = [1, 2, 3, 6]
sol = Solution()
res = sol.canPartition(nums)
print('==res:', res)思路2:优化版 用一维数组替代,只不过采用逆序
其中dp[j] = dp[j] || dp[j - nums[i]] 可以理解为 dp[j] (新)= dp[j] (旧) || dp[j - nums[i]] (旧),如果采用正序的话 dp[j - nums[i]]会被之前的操作更新为新值
import numpy as np
#转换成0 1背包问题 找到数组和的一半的子集
#优化版
#dp[j] = [j]#不选择nums[i]
#dp[j] = dp[j-nums]#选择nums[i]
# #如果 j<nums[i] dp[i][j] = dp[i-1][j]
class Solution:
def canPartition(self, nums):
# nums = sorted(nums)
# print('==nums:', nums)
n = len(nums)
if n<2:#数组长度无法划分
return False
sum_ = sum(nums)
max_value = max(nums)
if sum_ % 2==1:#奇数的话没法拆分
return False
target = sum_//2
if max_value>target:#最大值大于一半了 不满足条件
return False
dp = [False for i in range(target+1)]
print('===np.array(dp):', np.array(dp))
#不选取任何正整数
dp[0] = True
dp[nums[0]] = True#i==0 只有一个正整数 nums[0] 可以被选取
for i in range(1, n):
for j in range(target, 0, -1):
if j<nums[i]:#j<nums[i]
dp[j] = dp[j]
else:#不选择nums[i]与选择nums[i]
dp[j] = dp[j] or dp[j-nums[i]]
print('===np.array(dp):', np.array(dp))
return dp[-1]
# nums = [1, 5, 11, 5]
nums = [1, 2, 3, 6]
sol = Solution()
res = sol.canPartition(nums)
print('==res:', res)78-1.路径总和
1.递归法
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution(object):
def hasPathSum(self, root, sum):
"""
:type root: TreeNode
:type sum: int
:rtype: bool
"""
if not root:
return False
if not root.left and not root.right and root.val==sum:
return True
sum -=root.val
return self.hasPathSum(root.left,sum) or self.hasPathSum(root.right,sum)
c++实现:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool hasPathSum(TreeNode* root, int targetSum) {
if(root == nullptr){
return false;
}
if (root->left == nullptr && root->right == nullptr && targetSum==root->val){
return true;
}
targetSum -=root->val;
return hasPathSum(root->left,targetSum) || hasPathSum(root->right,targetSum);
}
};2.利用栈--DFS
class Solution(object):
def hasPathSum(self, root, sum):
"""
:type root: TreeNode
:type sum: int
:rtype: bool
"""
# # #递归终止条件
# if root is None:
# return False
# if root.left is None and root.right is None and root.val == sum:
# return True
# sum = sum - root.val
# # print('===sum:', sum)
# return self.hasPathSum(root.left, sum) or self.hasPathSum(root.right, sum)
if not root:
return False
quene = [(root, root.val)]
while quene:
node,value = quene.pop()
if node.left is None and node.right is None and value==sum:
return True
if node.left is not None:
quene.append((node.left,value+node.left.val))
if node.right is not None:
quene.append((node.right,value+node.right.val))
# print('==quene:',quene)
return False3.利用队列--BFS
class Solution(object):
def hasPathSum(self, root, sum):
"""
:type root: TreeNode
:type sum: int
:rtype: bool
"""
# # #递归终止条件
# if root is None:
# return False
# if root.left is None and root.right is None and root.val == sum:
# return True
# sum = sum - root.val
# # print('===sum:', sum)
# return self.hasPathSum(root.left, sum) or self.hasPathSum(root.right, sum)
if not root:
return False
quene = [(root, root.val)]
while quene:
node,value = quene.pop(0)
if node.left is None and node.right is None and value==sum:
return True
if node.left is not None:
quene.append((node.left,value+node.left.val))
if node.right is not None:
quene.append((node.right,value+node.right.val))
# print('==quene:',quene)
return False78-2:路径总和 II
思路:回溯 这种里面要调用两层回溯的 track就不要放在递归函数里面了
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def dfs(self, node, sum_):
if node is None:
return 0
store = self.track.copy()
self.track.append(node.val)
# print('==self.track:', self.track)
if node.left is None and node.right is None and sum_==node.val:
self.res.append(self.track)
sum_ -= node.val
self.dfs(node.left, sum_)
self.dfs(node.right, sum_)
# self.track.pop()
self.track = store
def pathSum(self, root: TreeNode, sum: int) -> List[List[int]]:
self.res = []
self.track = []
self.dfs(root, sum)
return self.resc++实现:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> res;
vector<int> track;
void dfs(TreeNode* root, int targetSum){
if(root==nullptr){
return ;
}
vector<int> store;
store = track;
track.push_back(root->val);
if(root->left==nullptr && root->right==nullptr && targetSum==root->val){
res.push_back(track);
}
targetSum -= root->val;
dfs(root->left, targetSum);
dfs(root->right, targetSum);
track = store;
}
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
dfs(root, targetSum);
return res;
}
};78-3:路径总和 III
思路:用一个列表存储从节点开始的数字和
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
#用列表记录从每一个节点开始的和
class Solution:
def dfs(self, node, sum_list, sum):
if node is None:
return 0
sum_list = [num+node.val for num in sum_list]
sum_list.append(node.val)
for num in sum_list:
if num==sum:
self.res+=1
self.dfs(node.left, sum_list, sum)
self.dfs(node.right, sum_list, sum)
def pathSum(self, root: TreeNode, sum: int) -> int:
self.res = 0
self.dfs(root, [], sum)
return self.resc++实现:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int res;
void dfs(TreeNode* node, vector<int> num_list, int sum){
if(node == nullptr){
return ;
}
for (int i=0; i<num_list.size(); i++){
num_list[i] += node->val;
}
num_list.push_back(node->val);
for(int i=0; i<num_list.size(); i++){
if(num_list[i]==sum){
res++;
}
}
dfs(node->left, num_list, sum);
dfs(node->right, num_list, sum);
}
int pathSum(TreeNode* root, int sum) {
vector<int> num_list;
dfs(root, num_list, sum);
return res;
}
};思路1:hash
#利用hash存储出现过得数字
class Solution:
def findDisappearedNumbers(self, nums):
dict_ = {}
for num in nums:
dict_[num] = dict_.get(num, 0)+1
print('==dict_:', dict_)
res =[]
for i in range(1, len(nums)+1):
if i not in dict_:
res.append(i)
return res
nums = [4,3,2,7,8,2,3,1]
sol = Solution()
res = sol.findDisappearedNumbers(nums)
print('==res:', res)
思路2:原地修改
#利用list原地进行修改
class Solution:
def findDisappearedNumbers(self, nums):
for i in range(len(nums)):
index = abs(nums[i]) - 1
if nums[index] > 0:
nums[index] *= -1
print('==nums:', nums)
res =[]
for i in range(len(nums)):
if nums[i]>0:
res.append(i+1)
return res
nums = [4,3,2,7,8,2,3,1]
# nums = [1, 3, 3, 4, 5]
sol = Solution()
res = sol.findDisappearedNumbers(nums)
print('==res:', res)思路:通过异或取得不同数的 在向右移动 依次与1进行& 获得1的个数
#思路:通过异或取得不同数的 在向右移动 依次与1进行& 获得1的个数
class Solution:
def hammingDistance(self, x, y):
res = x ^ y#异或取得不同的数 异或 相同为0 不同为1
# print('==res:', res)
dis = 0
while res:#向右移位
# print('==res&1:', res&1)
if res&1:
dis+=1
res = res>>1
# print('==res:', res)
return dis
x = 1
y = 4
sol = Solution()
sol.hammingDistance(x, y)
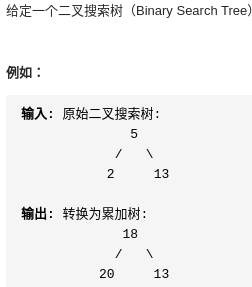
思路:其实就是逆中序遍历,利用二叉搜索树的特点,跟节点值更新为右孩子和根节点值之和,左孩子值更新为根节点与左孩子值之和。
1.迭代法:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def convertBST(self, root: TreeNode) -> TreeNode:
stack = []
node = root
value = 0
while stack or node:
while node:#把跟节点与右子树节点依次压进栈 实现逆中序遍历
stack.append(node)
node = node.right
print('==stack:', stack)
node = stack.pop()
print('==node:',node)
value += node.val
node.val = value
print('==node.left:', node.left)
node = node.left
return root
2.递归法:
其中res存储逆中序遍历(右根左)的值,便于查看
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def helper(self, node):
if node:
self.helper(node.right)
# self.res.append(node.val)
self.value+=node.val
node.val = self.value
self.helper(node.left)
def convertBST(self, root: TreeNode) -> TreeNode:
# self.res =[]
self.value = 0
self.helper(root)
return rootc++实现:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int res = 0;
void help(TreeNode* node){
if(node == nullptr){
return ;
}
help(node->right);
res += node->val;
node->val = res;
help(node->left);
}
TreeNode* convertBST(TreeNode* root) {
help(root);
return root;
}
};82.二叉树的直径
思路:递归函数用来获取每一层深度,然后在分别对左右子树深度求和,这里要注意的是最长直径不一定过根节点,所有要用一个变量存储遍历每个节点时的最大直径.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def get_depth(self, node):
if node is None:
return 0
l = self.get_depth(node.left)
r = self.get_depth(node.right)
self.max_value = max(self.max_value, l+r)
return max(l,r)+1
def diameterOfBinaryTree(self, root: TreeNode) -> int:
self.max_value = 0
if root is None:
return 0
self.get_depth(root)
return self.max_valuec++实现:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int max_value=0;
int help(TreeNode* node){
if(!node){
return 0;
}
int l = help(node->left);
int r = help(node->right);
max_value = max(max_value, l+r);
return max(l,r)+1;
}
int diameterOfBinaryTree(TreeNode* root) {
help(root);
return max_value;
}
};83.和为K的子数组
思路1:枚举(超时) O(n2)
class Solution:
def subarraySum(self, nums, k):
res=0
for i in range(len(nums)):
tmp = 0
for j in range(i,len(nums)):
tmp+=nums[j]
if tmp==k:
res+=1
print('=res:',res)
return res
# nums = [1,1,1]
# k = 2
nums = [1,-1,0]
k = 0
sol = Solution()
sol.subarraySum(nums, k)
思路2:hash,利用字典的key值存储累加和,value值存储出现次数
#利用字典 key存储累加的数字 value为出现的次数
class Solution:
def subarraySum(self, nums, k):
count_dict = {}
count, sum_ = 0, 0
for num in nums:
sum_+=num
if sum_==k:
count+=1
if sum_-k in count_dict:
count+=count_dict[sum_-k]
if sum_ in count_dict:
count_dict[sum_]+=1
else:
count_dict[sum_]=1
print('==count_dict:', count_dict)
print('count:', count)
return count
nums = [1, 1, 1]
k = 2
# nums = [1, -1, 1]
# k = 0
sol = Solution()
sol.subarraySum(nums, k)思路1:单调递增栈
class Solution:
def findUnsortedSubarray(self, nums):
#找到递增的拐点
stack = []
left = len(nums)-1
for i in range(len(nums)):
while stack and nums[i] < nums[stack[-1]]:
index = stack.pop()
left = min(left, index)
stack.append(i)
print('==stack:', stack)
print('left:', left)
#找到逆序递增的拐点
stack = []
right = 0
for i in range(len(nums)-1, -1, -1):
while stack and nums[i] > nums[stack[-1]]:
index = stack.pop()
right = max(right, index)
stack.append(i)
print('==right:', right)
return right-left+1 if right-left>0 else 0
nums = [2, 6, 4, 8, 10, 9, 15]
# nums = [2, 1, 6]
# nums = [1, 2]
# nums = [2, 1]
# nums = [5, 4, 3, 2, 1]
sol = Solution()
res = sol.findUnsortedSubarray(nums)
print('======res:', res)思路2:排序
class Solution:
def findUnsortedSubarray(self, nums: List[int]) -> int:
# print('==nums:', nums)
sort_nums = sorted(nums)
# print('==sort_nums:', sort_nums)
left = len(nums) - 1
right = 0
for i in range(len(nums)):
if nums[i] != sort_nums[i]:
left = min(left, i)
right = max(right, i)
# print('==left:', left)
# print('==right:', right)
return right - left + 1 if right - left > 0 else 085.合并二叉树
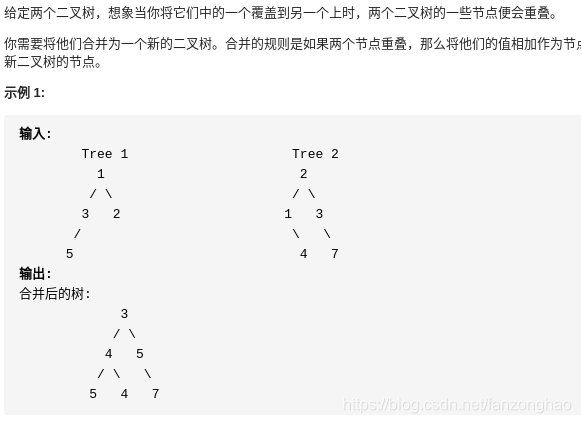
思路:采用前序遍历访问二叉树,如果节点其一为none,就返回另一个
1.递归法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def mergeTrees(self, t1: TreeNode, t2: TreeNode) -> TreeNode:
if t1 is None:
return t2
if t2 is None:
return t1
t1.val+=t2.val
t1.left = self.mergeTrees(t1.left,t2.left)
t1.right = self.mergeTrees(t1.right,t2.right)
return t1
2.迭代法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def mergeTrees(self, t1: TreeNode, t2: TreeNode) -> TreeNode:
if t1 is None:
return t2
stack= [(t1,t2)]
while stack:
t = stack.pop()
if t[0] is None or t[1] is None:
continue
t[0].val +=t[1].val
if t[0].left is None:
t[0].left = t[1].left
else:
stack.append((t[0].left, t[1].left))
if t[0].right is None:
t[0].right = t[1].right
else:
stack.append((t[0].right, t[1].right))
return t1
c++实现:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
if(root1 == nullptr){
return root2;
}
if(root2 == nullptr){
return root1;
}
root1->val += root2->val;
root1->left = mergeTrees(root1->left, root2->left);
root1->right = mergeTrees(root1->right, root2->right);
return root1;
}
};86.任务调度器
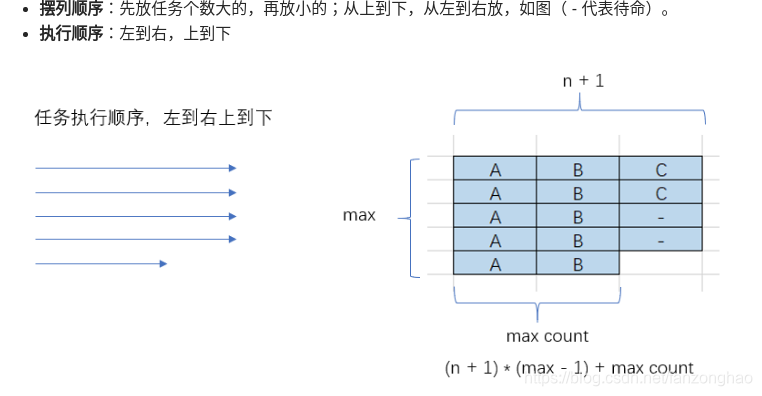
思路: 贪心 填桶法
class Solution(object):
def leastInterval(self, tasks, n):
"""
:type tasks: List[str]
:type n: int
:rtype: int
"""
length = len(tasks)
if length <= 1:
return length
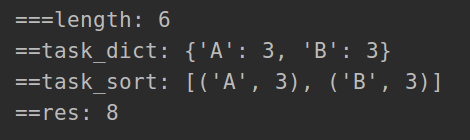
print('===length:', length)
# 用于记录每个任务出现的次数
task_dict = {}
for task in tasks:#不存在task时 返回0
task_dict[task] = task_dict.get(task,0)+1
print('==task_dict:', task_dict)
# 按任务出现的次数从大到小排序
task_sort = sorted(task_dict.items(), key=lambda x: x[1], reverse=True)
print('==task_sort:', task_sort)
# # 出现最多次任务的次数
max_task_count = task_sort[0][1]
# 至少需要的最短时间
res = (max_task_count - 1) * (n + 1)
for sort in task_sort:
if sort[1] == max_task_count:
res += 1
print('==res:', res)
# # 如果结果比任务数量少,则返回总任务数
return res if res >= length else length
tasks = ["A","A","A","B","B","B"]
n = 2
# n = 0
sol = Solution()
sol.leastInterval(tasks, n)87-1.回文子串
思路1:两层for循环遍历进行判断是否是回文字符串即可,超出时间限制
#双层for循环超出时间限制
class Solution:
def judge_palindrome(self, s):
l = 0
r = len(s) -1
while l<=r:
if s[l]==s[r]:
l+=1
r-=1
else:
return False
return True
def countSubstrings(self, s):
res=0
for i in range(len(s)):
# print('==i:', i)
for j in range(i, len(s)):
# print('==j', j)
# print('==s[i:j+1]:', s[i:j+1])
if self.judge_palindrome(s[i:j+1]):
res += 1
return res
# s = "abc"
s = "aaa"
sol = Solution()
res = sol.countSubstrings(s)
print('==res:', res)
思路2,中心枚举,专门用self.res存储 left与righe索引方便查看,,最后求和就是会文字符串的个数。
import numpy as np
class Solution:
def helper(self,left,right,s):
while left>=0 and right<len(s) and s[left]==s[right]:
self.res[left][right]=1
self.fin_res+=1
left-=1
right+=1
def countSubstrings(self, s):
self.res = [[0 for i in range(len(s)) ] for i in range(len(s))]
self.fin_res = 0
for i in range(len(s)):
self.helper(i,i,s)
self.helper(i,i+1,s)
print(np.array(self.res))
return self.fin_res
s = "aaa"
sol = Solution()
sol.countSubstrings(s)87-2:回文串分割 IV
思路:中心枚举 用一个矩阵存储回文字符串左右索引的值,最后看看是不是分为三段即可
import numpy as np
class Solution:
def helper(self,left,right,s):
while left>=0 and right<len(s) and s[left]==s[right]:
self.res[left][right] = 1
left-=1
right+=1
def checkPartitioning(self, s):
length = len(s)
self.res = [[0 for _ in range(length)]for _ in range(length)]
for i in range(length):
self.helper(i, i, s)
self.helper(i, i+1, s)
print(np.array(self.res))
for i in range(length):
for j in range(i+1, length):
if self.res[0][i] and self.res[i+1][j] and self.res[j+1][length-1]:
return True
return False
# s = "abcbdd"
s = "bcbddxy"
# s = "juchzcedhfesefhdeczhcujzzvbmoeombv"
sol = Solution()
res = sol.checkPartitioning(s)
print('==res:', res)87-3.最长回文子串
class Solution:
def helper(self,left,right,s):
while left>=0 and right<len(s) and s[left]==s[right]:
left-=1
right+=1
if len(s[left+1:right])>len(self.res):
self.res = s[left+1:right]
def longestPalindrome(self, s: str) -> str:
self.res = ''
for i in range(len(s)):
self.helper(i,i,s)
self.helper(i,i+1,s)
return self.res
class Solution(object):
def monotoneIncreasingDigits(self, N):
"""
:type N: int
:rtype: int
"""
digits = []
A = list(map(int, str(N)))
# print('==A:', A)
for i in range(len(A)):
for d in range(1, 10):
# print('==digits + [d] * (len(A) - i):', digits + [d] * (len(A) - i))
if digits + [d] * (len(A) - i) > A:
digits.append(d - 1)
break
else:
digits.append(9)
# print('==digits:', digits)
return int("".join(map(str, digits)))88-2:每日温度
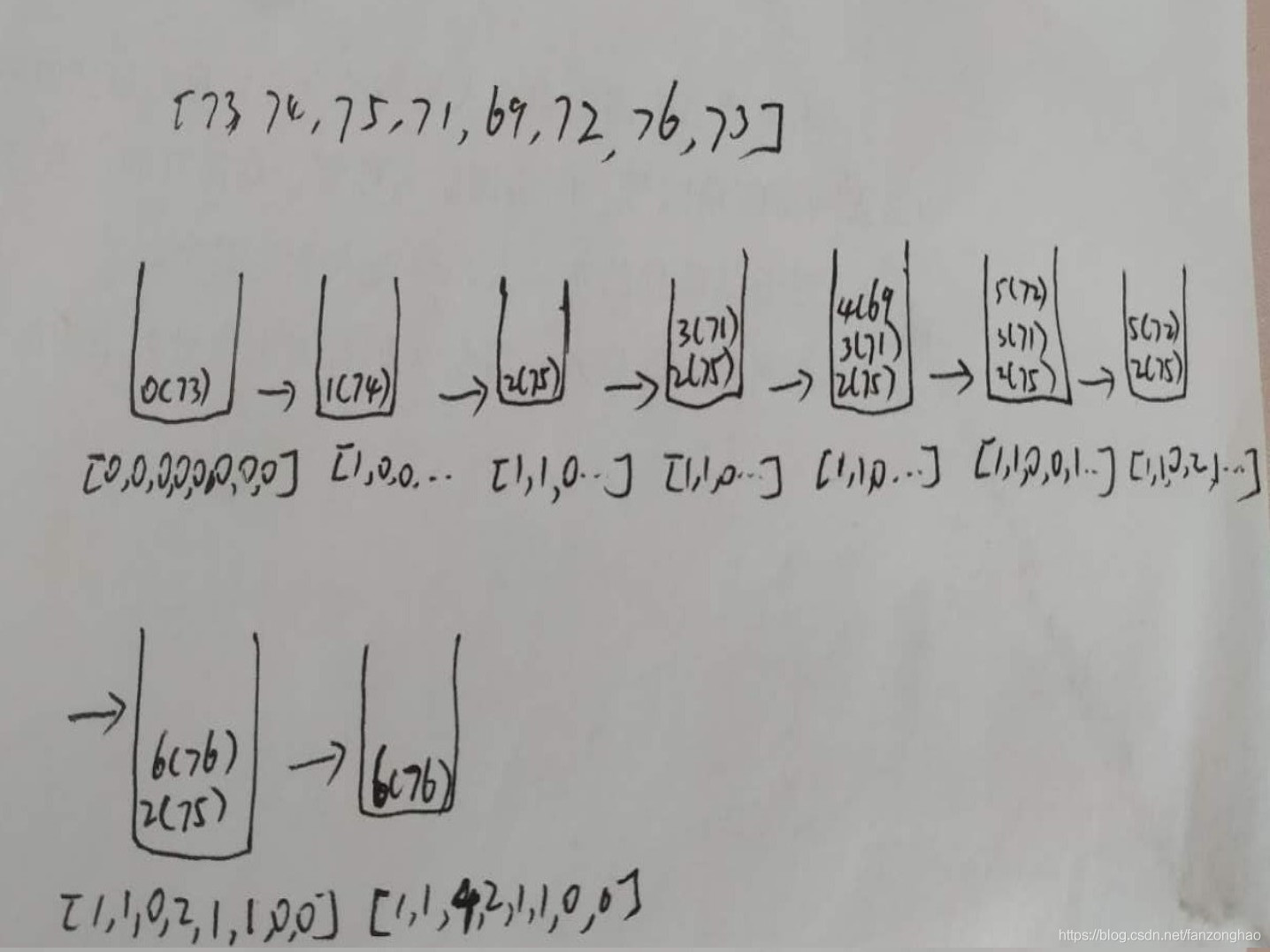
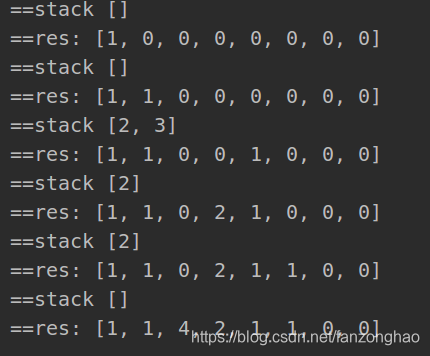
思路:单调递增栈
class Solution:
def dailyTemperatures(self, T):
#单调递增栈
res = [0]*len(T)
stack = []
for i in range(len(T)):
while stack and T[i] > T[stack[-1]]:
res[stack[-1]] = i - stack[-1]
stack.pop()
print('==stack', stack)
print('==res:', res)
stack.append(i)
return res
T = [73, 74, 75, 71, 69, 72, 76, 73]
sol = Solution()
sol.dailyTemperatures(T)