目录
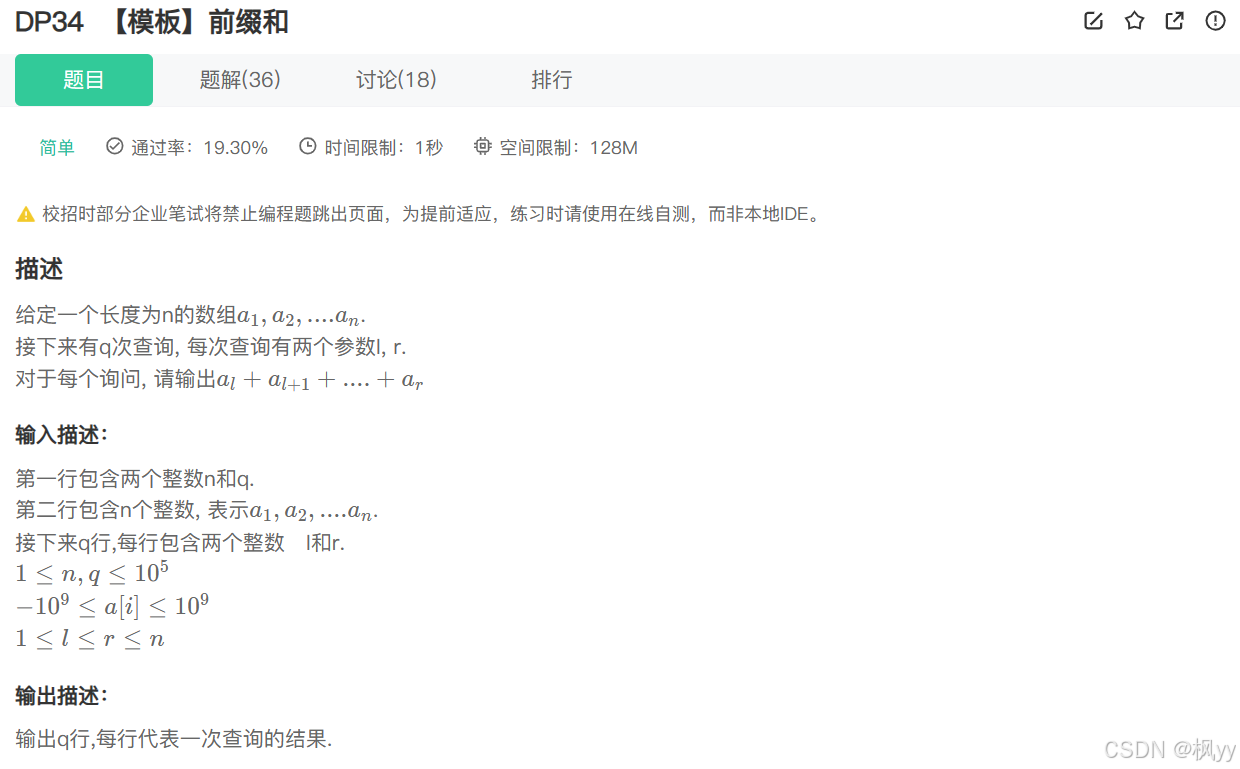
【模板】一维前缀和
如果我们用暴力解法,每次都要遍历一遍数组,一共遍历q次,这样时间复杂度太高,这时候我们构造一个前缀和数组,将1 - n区间内各区间的和存入进去,需要前n项和直接访问dp前缀和数组的下标位置即可。代码如下:
#include<iostream>
#include<vector>
using namespace std;
int main()
{
// 读入数据
int n, q; cin >> n >> q;
// n + 1 添加了虚拟节点0
vector<int> arr(n + 1); // 默认全部为0
for (int i = 1; i <= n; i++)
cin >> arr[i];
// 预处理出一个前缀和数组
vector<long long> dp(n + 1); // 防止溢出
for (int i = 1; i <= n; i++)
dp[i] = dp[i - 1] + arr[i];
// 使用前缀和数组
int l = 0, r = 0;
while (q--)
{
cin >> l >> r;
cout << dp[r] - dp[l - 1] << endl;
}
return 0;
}【模板】二维前缀和
预处理一个前缀和矩阵,将(1,1)到(i,j)位置的所有元素和存在这个dp数组中,通过面积计算方法,求出最终答案,代码如下:
int main()
{
// 读入数据
int n, m, q; cin >> n >> m >> q;
vector<vector<int>> arr(n + 1, vector<int>(m + 1));
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
cin >> arr[i][j];
// 预处理一个前缀和数组
vector<vector<long long>> dp(n + 1, vector<long long>(m + 1)); // 防止溢出
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + arr[i][j] - dp[i - 1][j - 1];
// 使用前缀和数组
while (q--)
{
int x1, y1, x2, y2; cin >> x1 >> y1 >> x2 >> y2;
cout << dp[x2][y2] - dp[x2][y1 - 1] - dp[x1 - 1][y2] + dp[x1 - 1][y1 - 1] << endl;
}
return 0;
}寻找数组的中心下标
注意边界情况,此处不需要开n+1个空间的前缀和数组,因为原数组中有一个元素要作为本题的中心下标,代码如下:
class Solution {
public:
int pivotIndex(vector<int>& nums) {
int n = nums.size();
vector<int> f(n), g(n);
// 预处理前缀和数组 从左向右
for (int i = 1; i < n; i++)
f[i] = f[i - 1] + nums[i - 1];
// 预处理后缀和数组 从右向左
for (int i = n - 2; i >= 0; i--)
g[i] = g[i + 1] + nums[i + 1];
for (int i = 0; i < n; i++)
{
if (g[i] == f[i])
return i;
}
return -1;
}
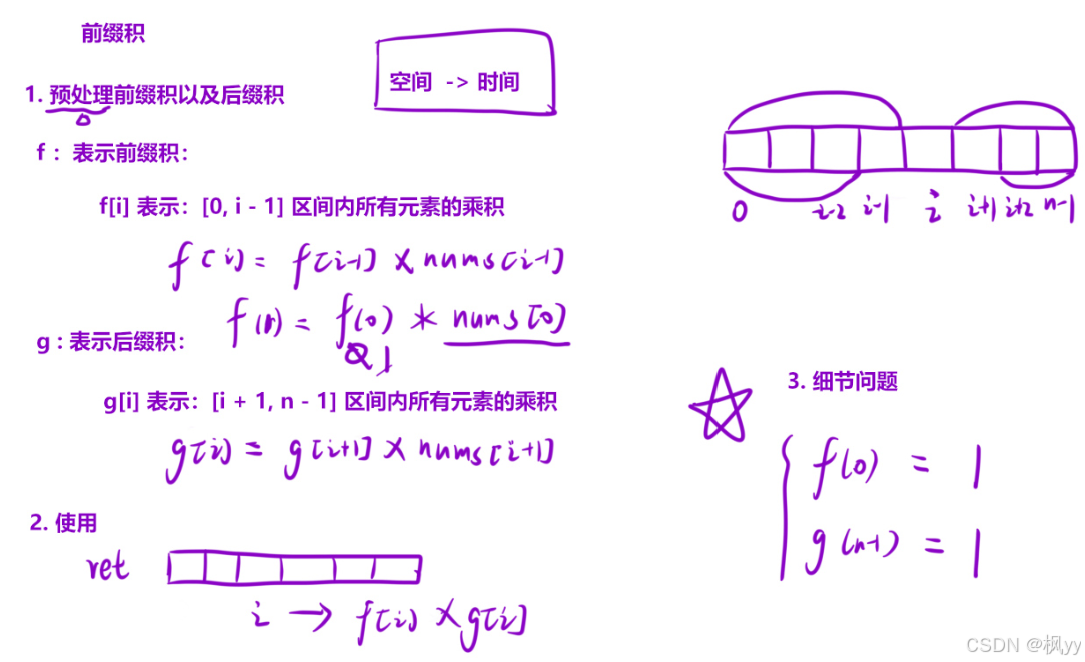
};除⾃⾝以外数组的乘积
和上题意思类似,不过要注意的是,边界情况f(0)和g(n-1)要初始化为1而不是0,代码如下:
class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
int n = nums.size();
vector<int> f(n), g(n), ret(n);
// 处理边界情况
f[0] = 1; g[n - 1] = 1;
// 预处理前缀积数组 从左向右
for (int i = 1; i < n; i++)
f[i] = f[i - 1] * nums[i - 1];
// 预处理后缀积数组 从右向左
for (int i = n - 2; i >= 0; i--)
g[i] = g[i + 1] * nums[i + 1];
for (int i = 0; i < n; i++)
ret[i] = f[i] * g[i];
return ret;
}
};
矩阵区域和
注意:二维前缀和数组要多开一行一列,否则会产生越界访问,此外dp数组和ans数组之间需要调整下标才能匹配位置,ans[ 0 ][ 0 ]对应的是dp [ 1 ][ 1 ]这个位置。代码如下:
class Solution {
public:
vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {
int m = mat.size(), n = mat[0].size(); // m 为行 n 为列
// 预处理一个二维前缀和数组 dp
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
for (int i = 1; i <= m; i++)
for (int j = 1; j <= n; j++)
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + mat[i - 1][j - 1] - dp[i - 1][j - 1];
// 存放答案的二维数组 ans
vector<vector<int>> ans(m, vector<int>(n));
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
int x1 = max(0, i - k) + 1, y1 = max(0, j - k) + 1;
int x2 = min(m - 1, i + k) + 1, y2 = min(n - 1, j + k) + 1;
ans[i][j] = dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1];
}
}
return ans;
}
};