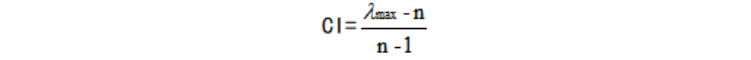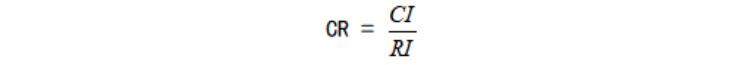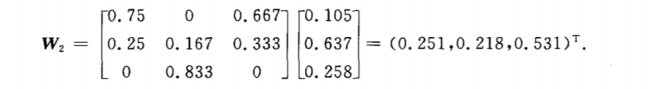| 时间 | 2020年4月15日 | 组别 | 数学建模 | 姓名 | Zkaisen |
|
本
周
完
成
作
总
结 | 本周我主要学习了层次分析法（AHP）的基本原理及其在企业资金分配方案、太阳镜产品质量评价等案例中的应用，并学习使用visio绘制所需图形以及了解maltab基础语法知识，并编程实现了一些功能。 01层次分析法概述 层次分析法是对定性问题进行定量分析的一种简便灵活而又实用的多准则决策方法。层次分析法是建模比赛中最基础的模型之一，其主要用于解决评价类问题。 02二层次分析法的特点 AHP的主要特点是通过建立递阶层次结构，把人类的判断转化到若干因素两两之间重要度的比较上，从而把难于量化的定性判断转化为可操作的重要度的比较上面。在许多情况下，决策者可以直接使用AHP进行决策，极大地提高了决策的有效性、可靠性和可行性。
03层次分析法的步骤和方法
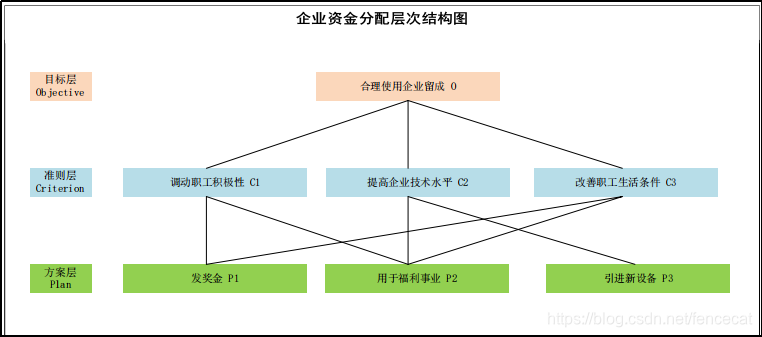
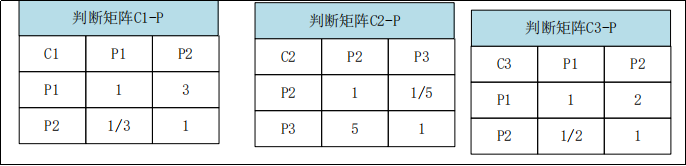
04结合企业应用案例，深入学习层次分析法 某企业年末又留成，希望将这笔资金用于以下几个领域：发奖金、福利事业和引进设备，但是再利用企业留成是需考虑以下及各方面：调动员工积极性、提高企业技术水平和改善职工生活条件。 1.分析系统中各因素之间的关系，建立系统的递阶层次结构 使用Visio生成，导出为PDF格式。 2.构造各层次中所有判断矩阵
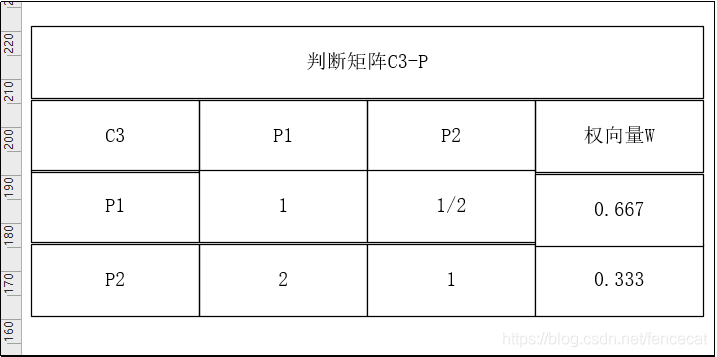
用成对比较法和1~9尺度，构造各层对上一层每一因素的成对比较矩阵。
3.由判断矩阵计算被比较元素对于该准则的相对权重并进行一致性检验
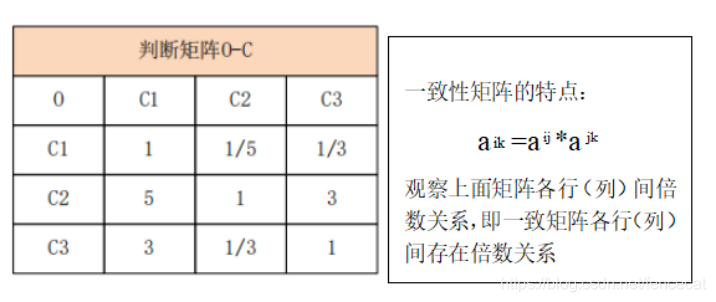
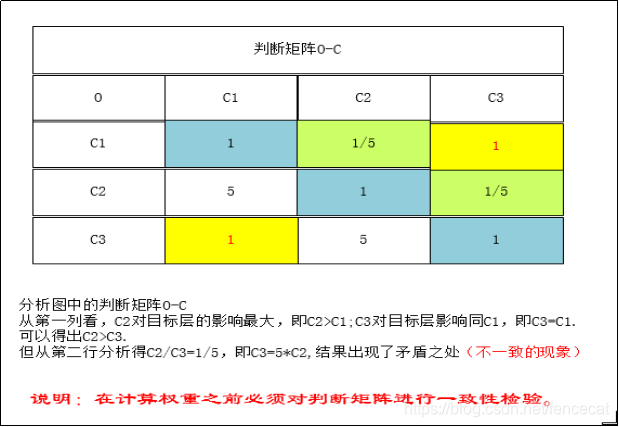
我们构造的判断矩阵都是正互反矩阵，若正互反矩阵满足
第一步 计算一致性指标 第二步 计算随机一致性指标RI
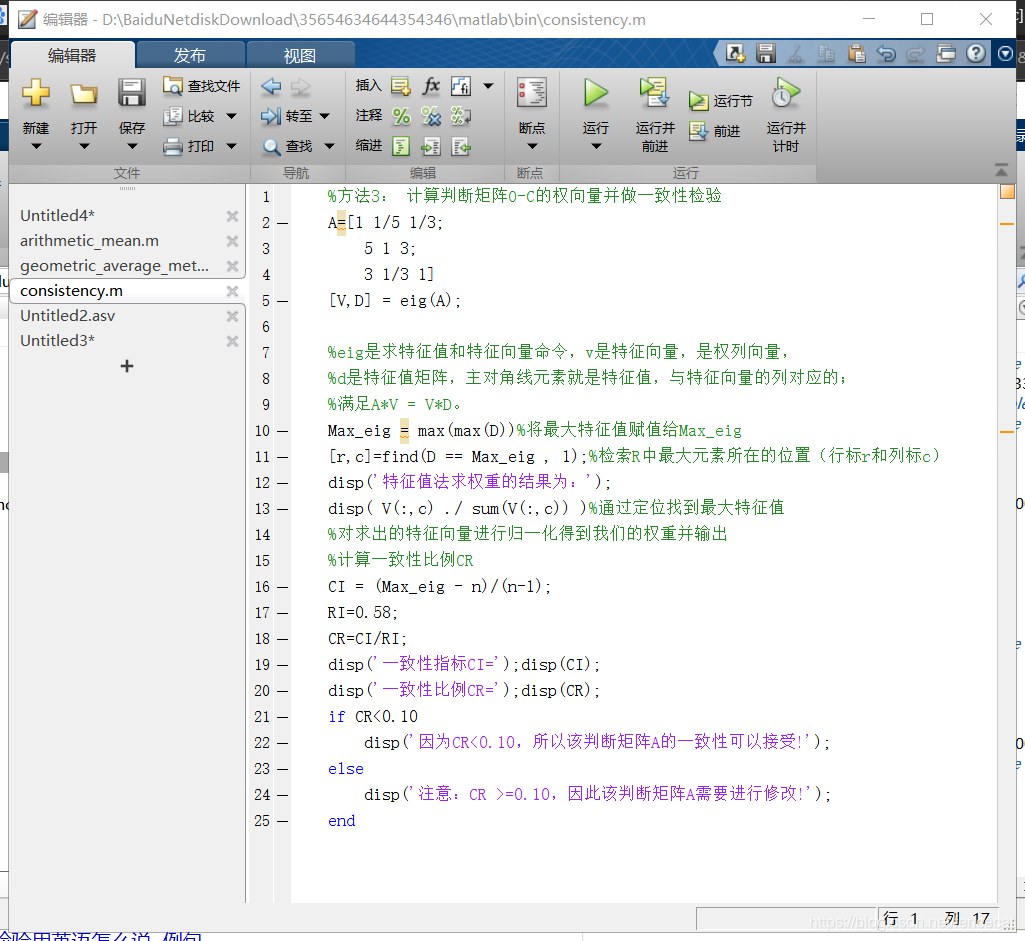
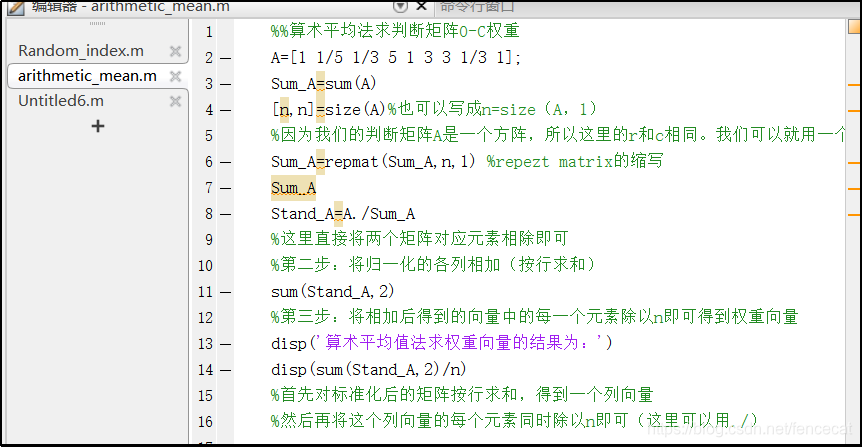
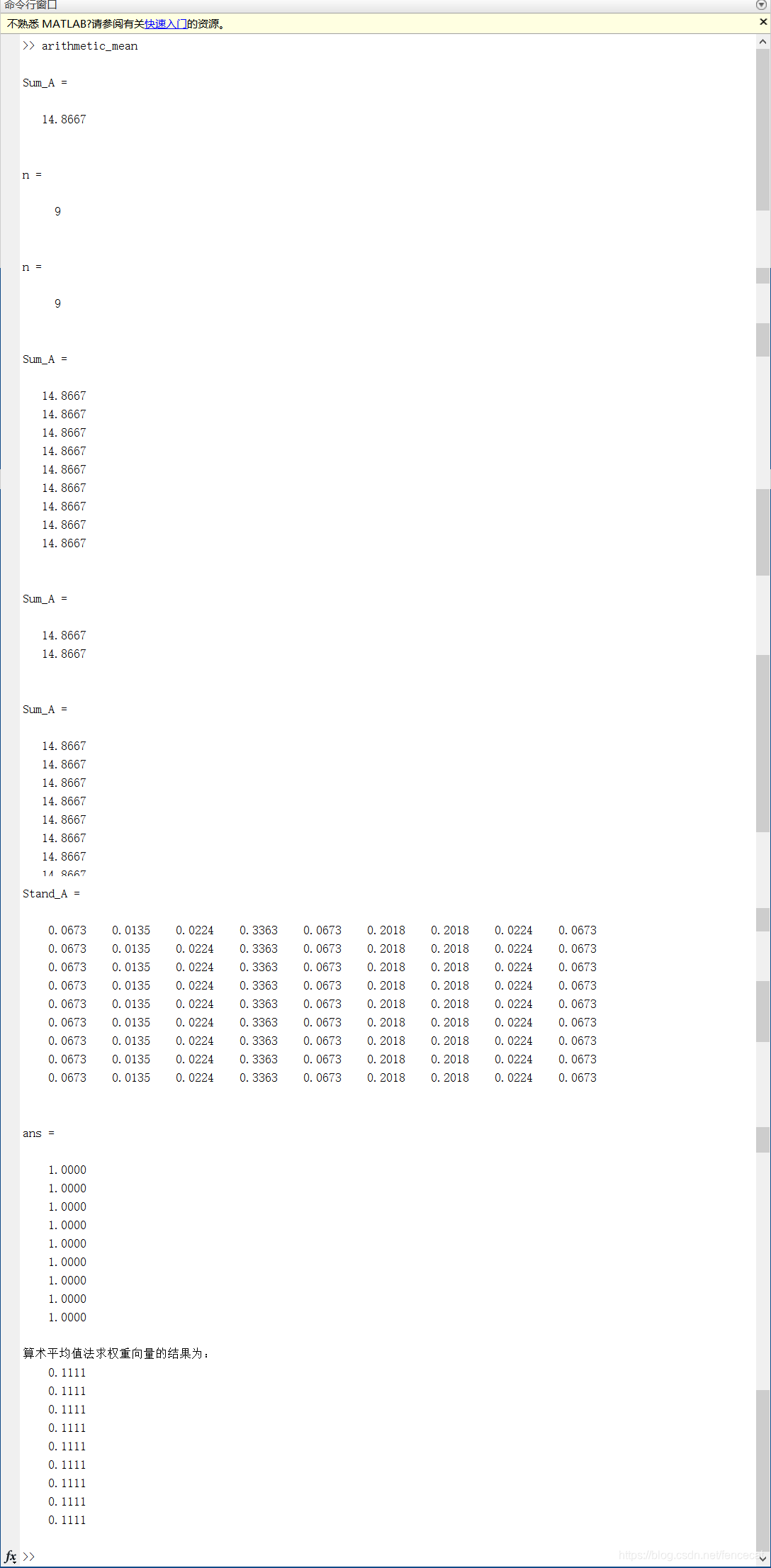
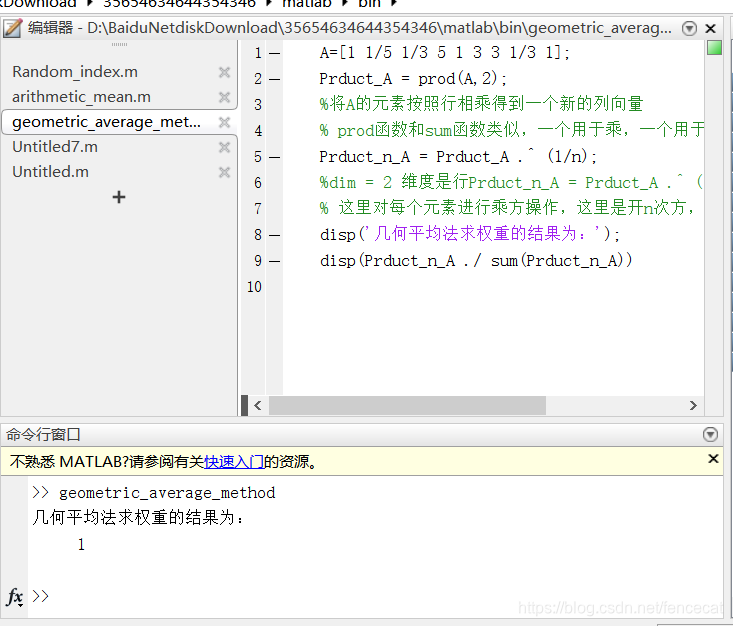
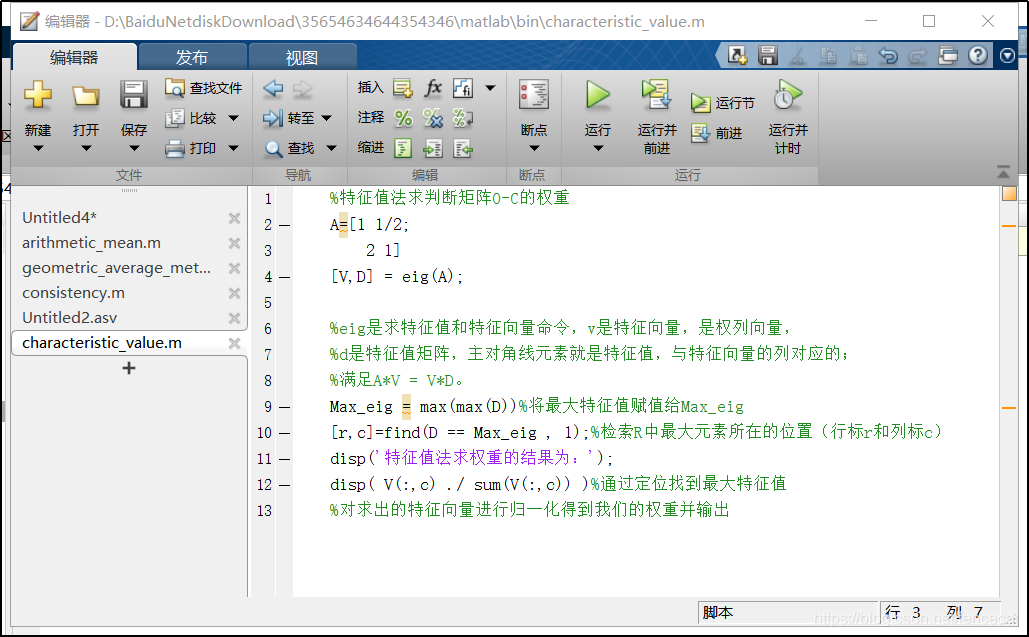
第三步 计算一致性比例CR 如果CR<0.1,则可以认为判断矩阵的一致性是可以接受的：否则需要对判断矩阵进行修正。修正的话，就是往一直矩阵上调整即调整判断矩阵各行成倍数关系。 4.MATLAB一致性检验代码及结果 5.计算被比较元素对于准则层的相对权重 方法一：：算术平均法 第一步：将判断矩阵按照列归一化（每一个元素除以其所在列的和） 第二步：将归一化的各列相加（按行求和） 第三步：将相加后的得到的向量中每一个元素除以n即可得到权重向量 MATLAB代码及运行结果： 方法二 几何平均法求权重 第一步：将判断矩阵按照行相乘得到一个新的列向量 第二步：将新的向量的每一个向量开n次方 第三步：对该向量进行归一化即可得到权重向量。 MATLAB代码及运行结果： 方法三：特征值法 假如我们的判断矩阵的一致性可以接受，那么我们可以仿照求一致矩阵权重的求法。 第一步：求出矩阵A的最大特征值以及它对应的特征向量。 第二步：对求出的特征向量进行归一化即可得到我们的权重。 MATLAB代码及运行结果： 6.计算各层元素对系统目标的合成权重，并进行排序。 最终的权重为准则层对目标层的权重向量与方案层对准则层的权重向量的乘积。
| ||||
|
所 遇 到 问 题 | 1.对代码中出现的函数不解时，打开帮助查看函数的详细讲解及示例 2.Prod函数：B = prod(A,dim)返回沿维度 dim 的乘积。例如，如果 A 为矩阵，则 prod(A,2) 为一个包含每一行乘积的列矢量。 3.repmat函数：B = repmat(A,m,n) %将矩阵A复制m×n块，即B由m×n块A平铺而成版。 4.需要加强对一致性检验中涉及线性代数的特征向量知识的理解 | ||||
|
备
注 | 我主要针对企业资金分配用层次分析法进行了实际操作，太阳镜产品质量评价中的层次分析是比较特殊的，它的方案层是准则层的子项，准则层的每个影响因素都各自对应有相应的方案层影响因素。 报告中的矩阵图用visio软件画 代码通过网络学习别人的代码，将代码跑起来并理解各部分的语义及其所实现功能。在理解的基础上把别人的代码做进一步修改，加入自己的理解，变成自己的知识。 | ||||
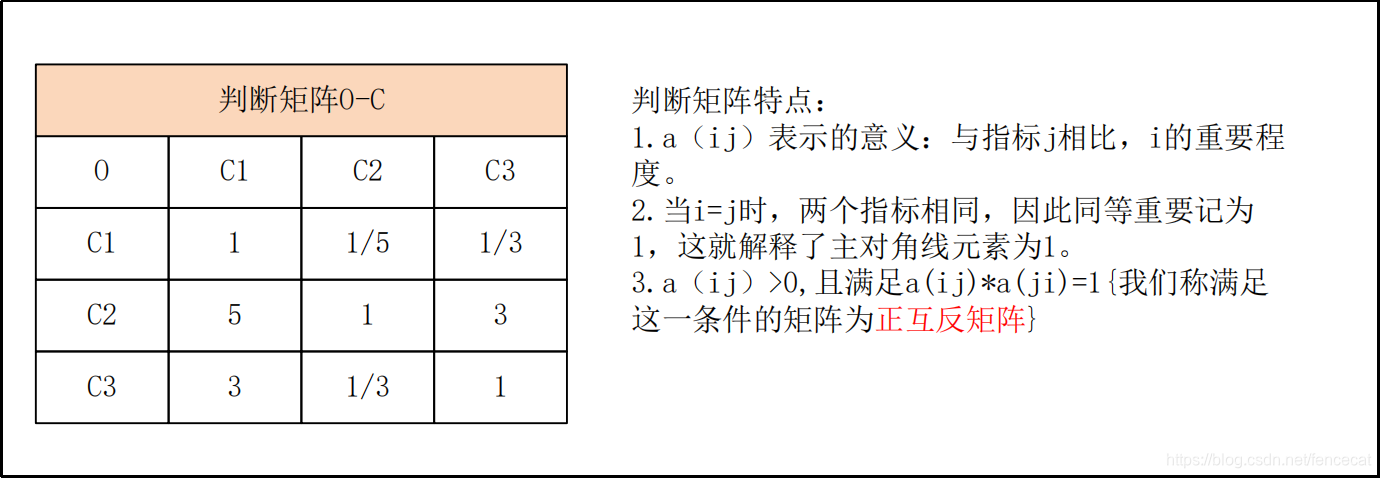
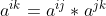为一致矩阵。
