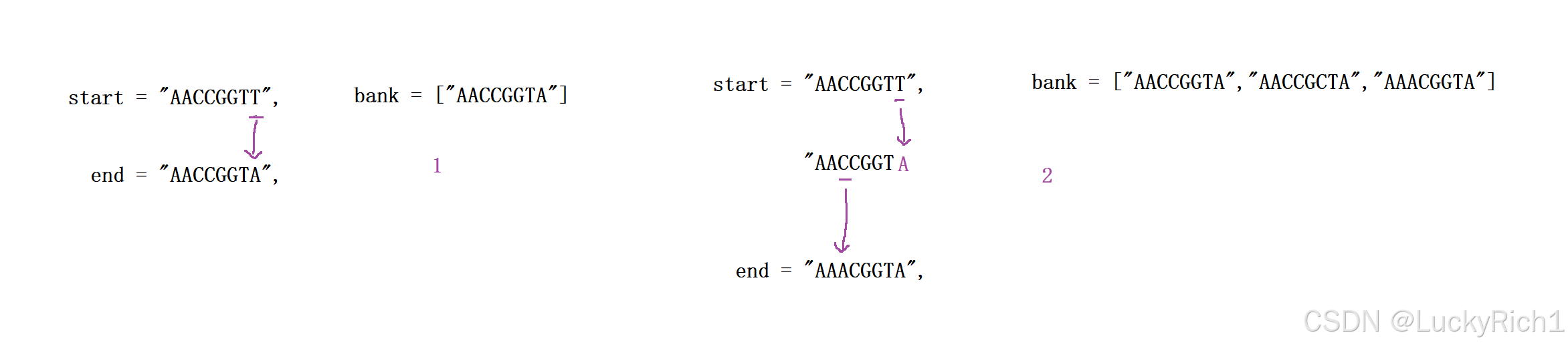点赞👍👍收藏🌟🌟关注💖💖
你的支持是对我最大的鼓励，我们一起努力吧!😃😃

1.最短路径问题简介

最短路径问题是图论里面最重要的问题，它里面最短路径问题包括单源最短路、多元最短路、边权为1的最短路、带负环的最短路等等。

这里我们只说 边权为 1 的最短路径问题

那什么是最短路径问题？
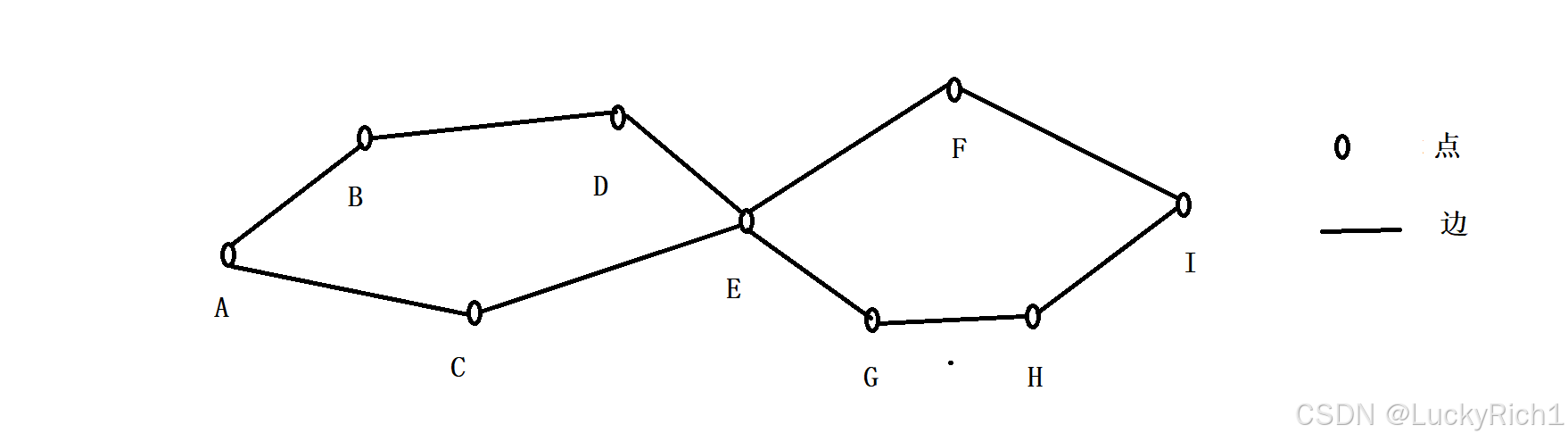
比如有一些地区，地区之间有道路相连，它会给一个起点，问到达另一个点最短的路径是多少？

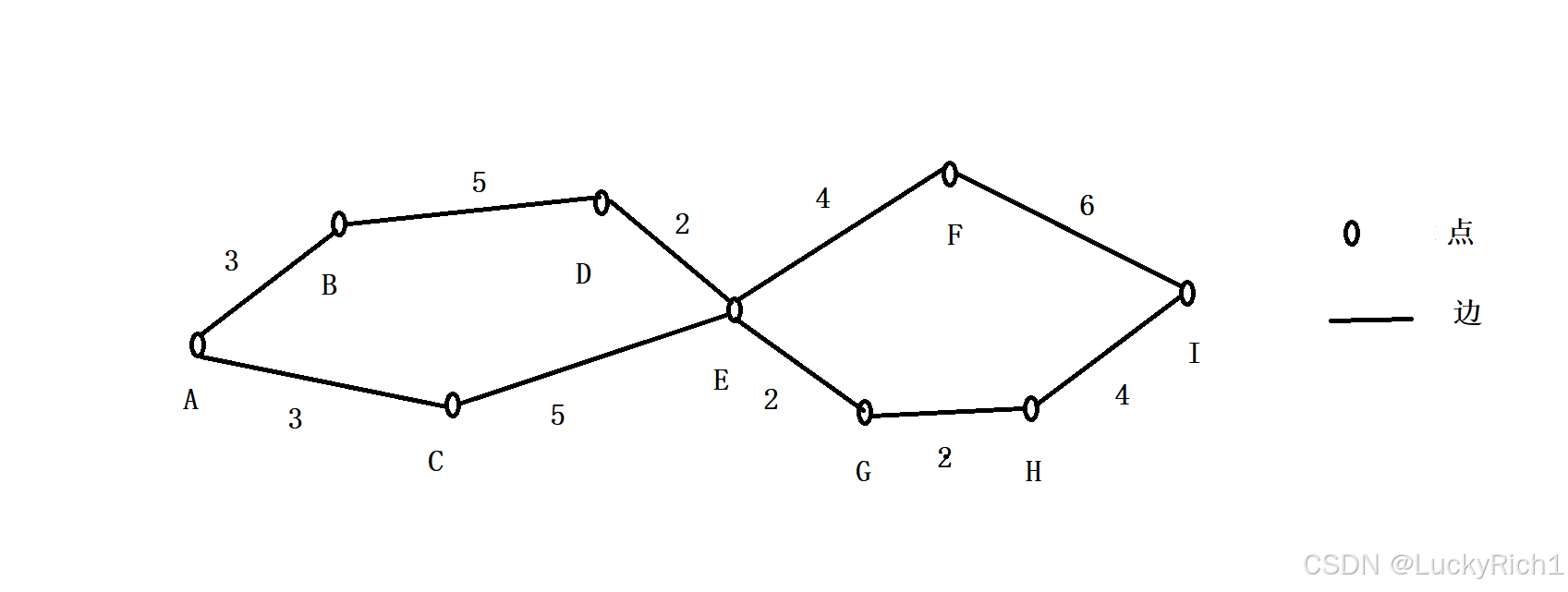
边上面可能赋予权值，权值可以理解为两个点之间的长度。然后有长度的时候问题你从 A->I 最短路径是多少？

但是这里我们不研究这种麻烦的最短路问题，我们只研究最简单最短路问题，边权都是为1的，意思是每一个边的权值都是相同的。 边权可以都为2、3、4等等，反正就是边权值都相同。

这类最短路问题怎么解决呢？
特别简单，从起点开始，来一次 BFS 即可。

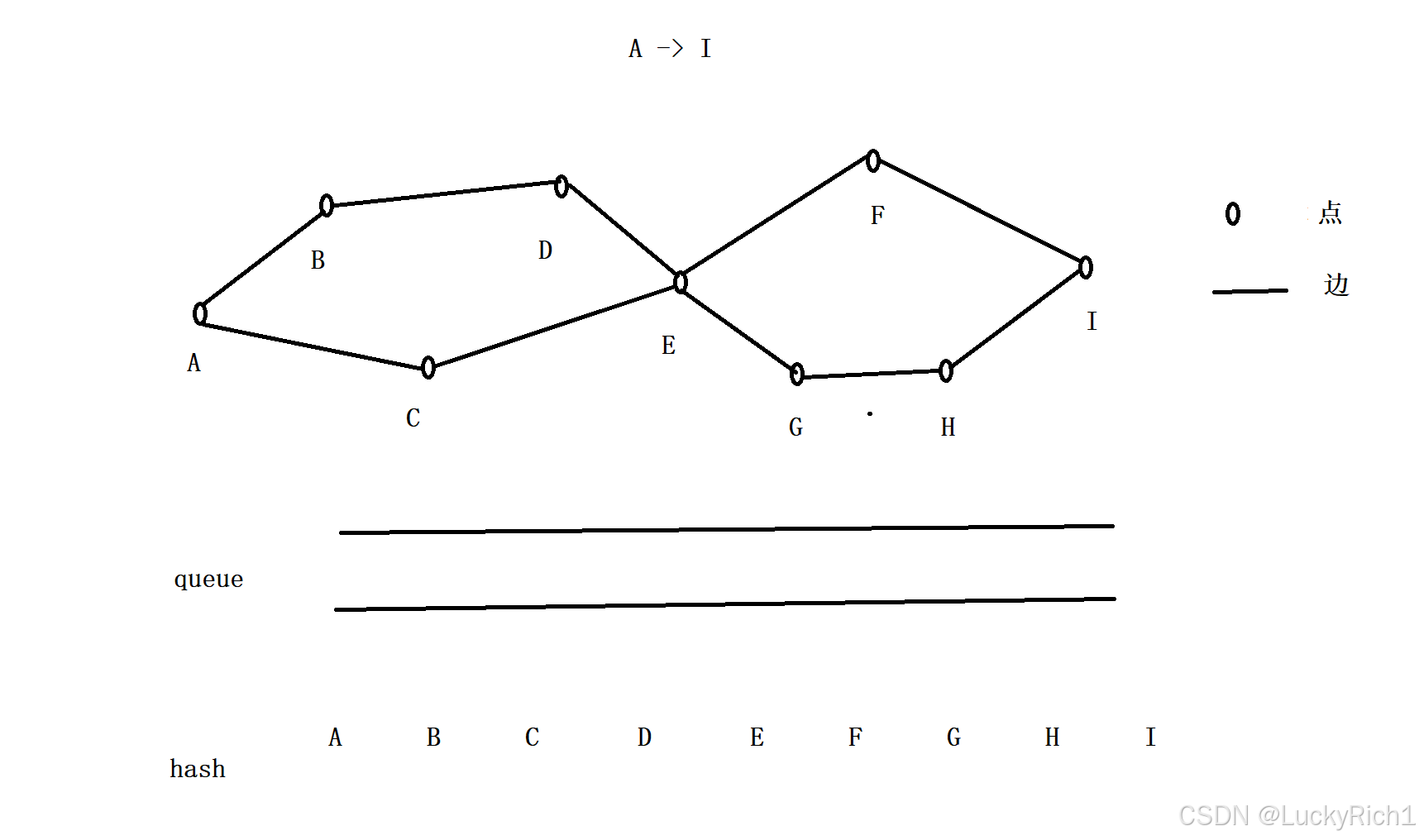
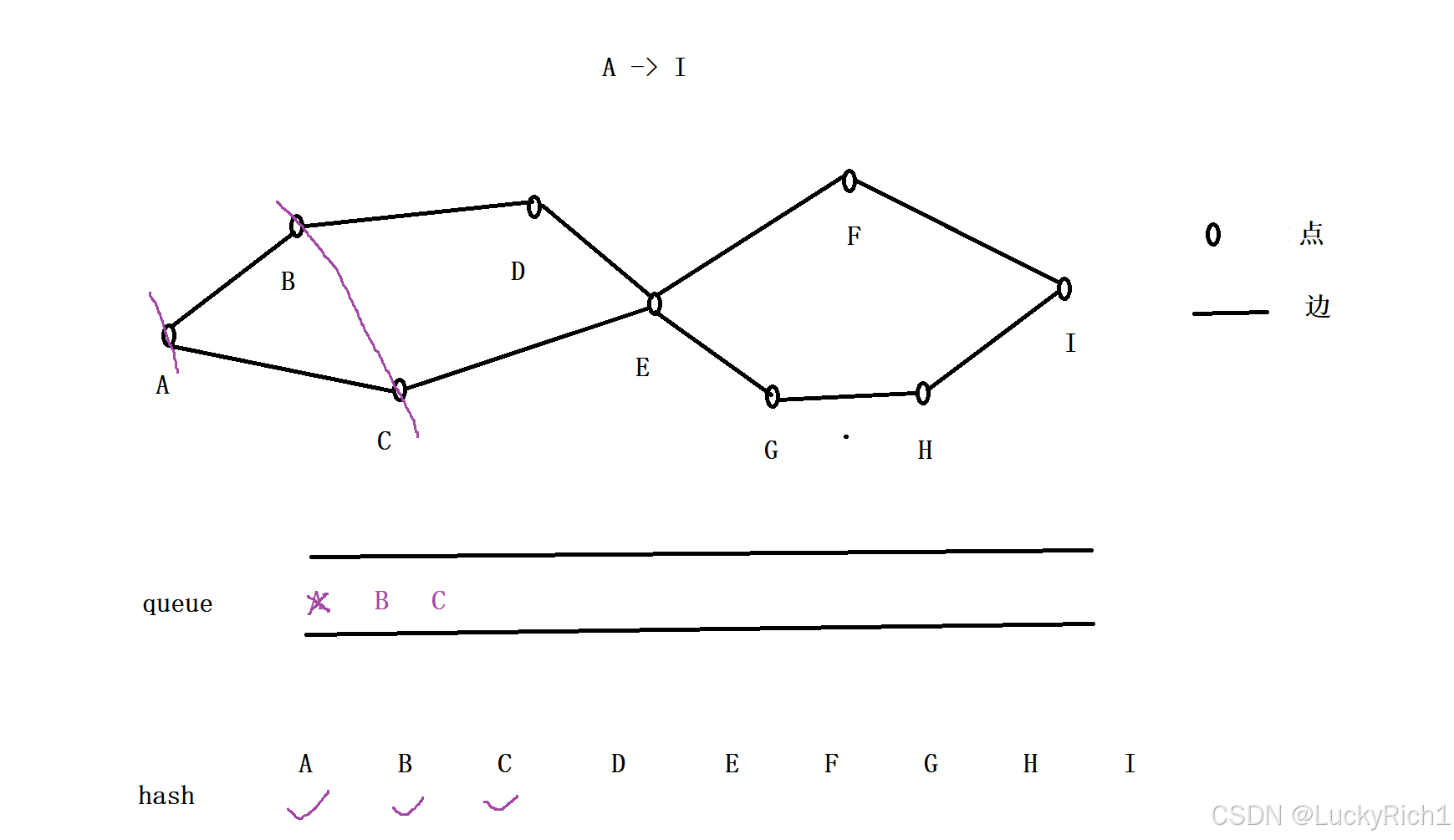
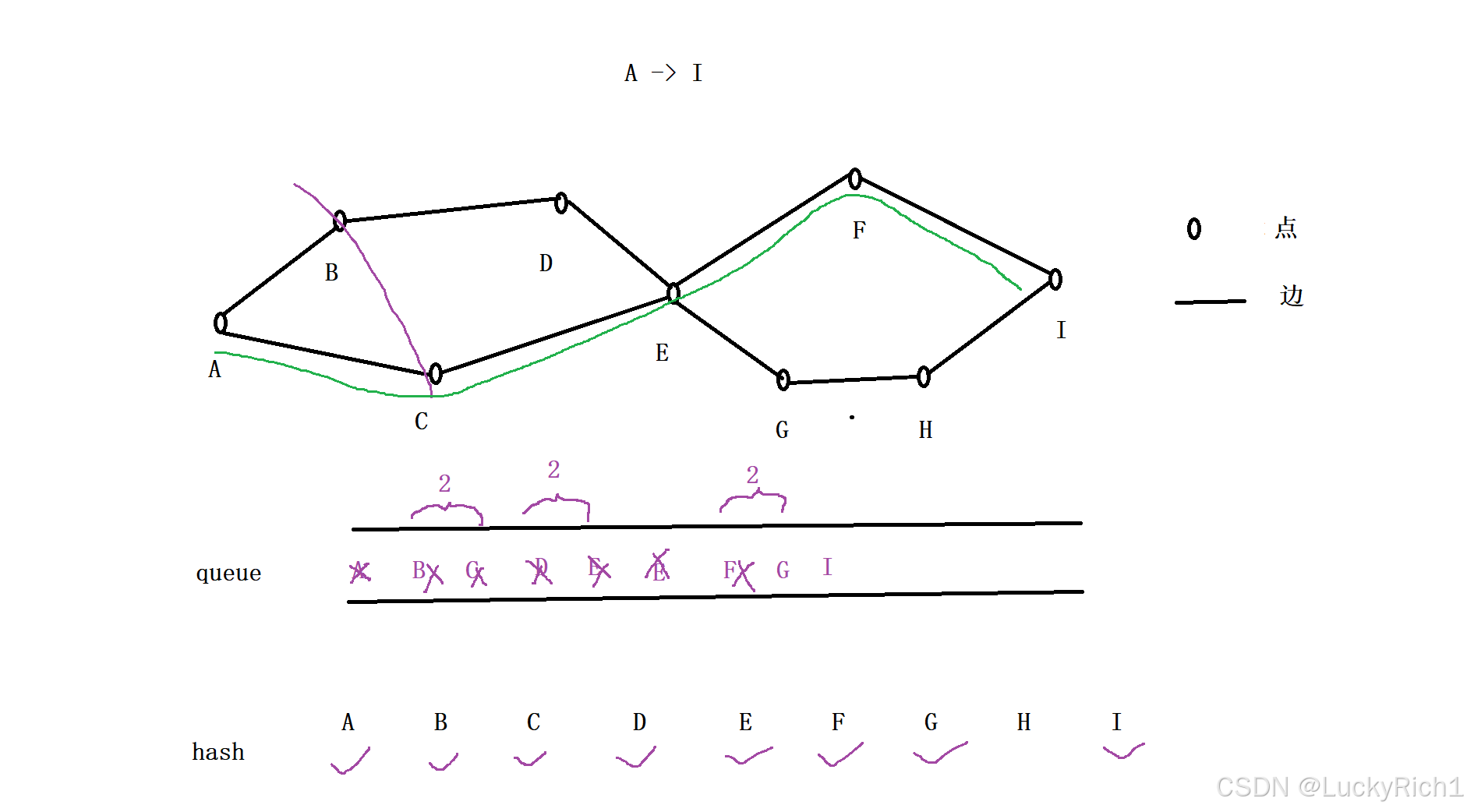
下面模拟一下，做 BFS 我们需要一个队列，还需要一个可以是hash表，也可以是数组来标记当前这个位置是否已经访问过！

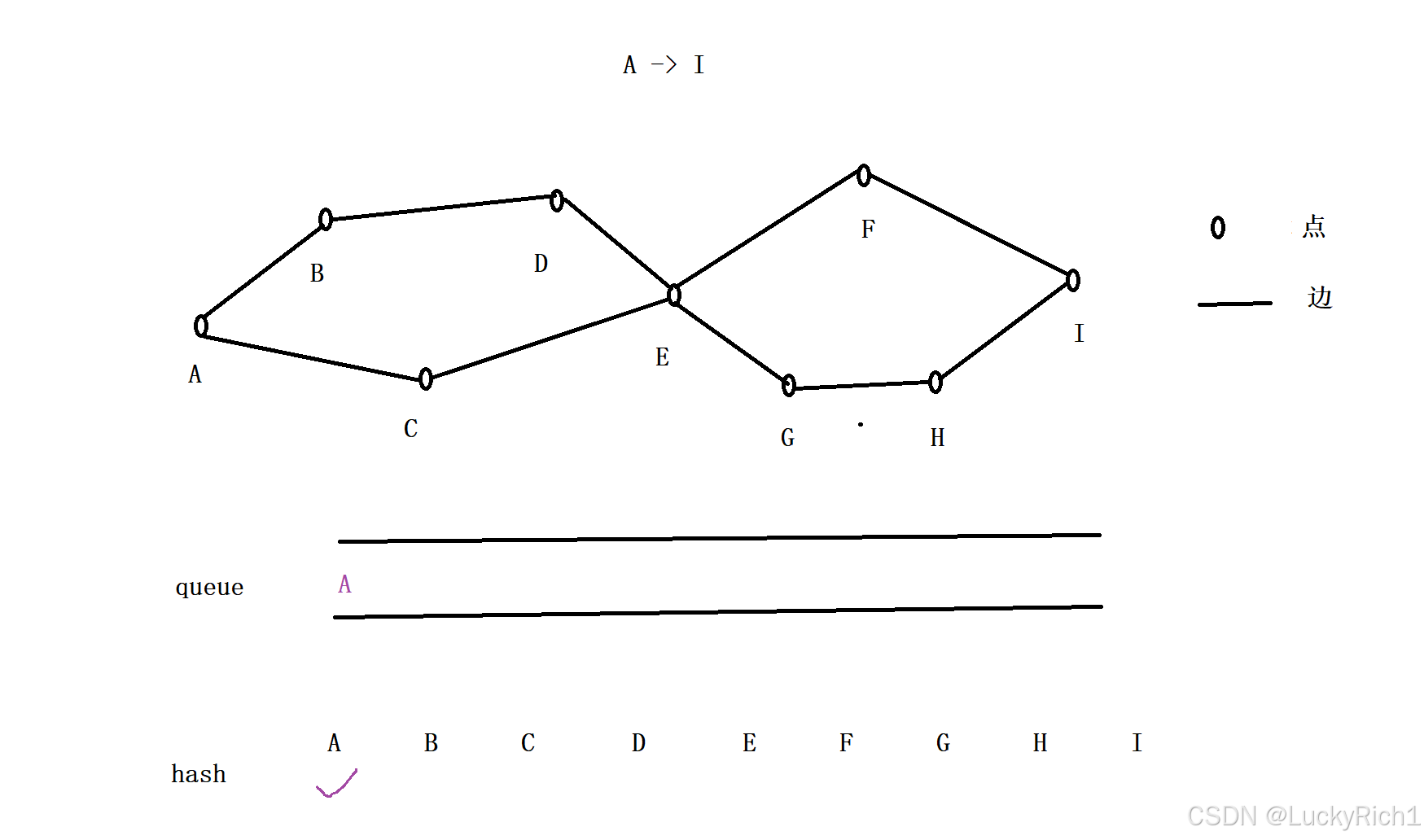
刚开始把起点丢入队列里面，并且在hash标记A已经被访问过。

接下里弹出队头元素，把队头元素能去的地方加入到队列。相当于在A这一层的基础上又往外扩了一层

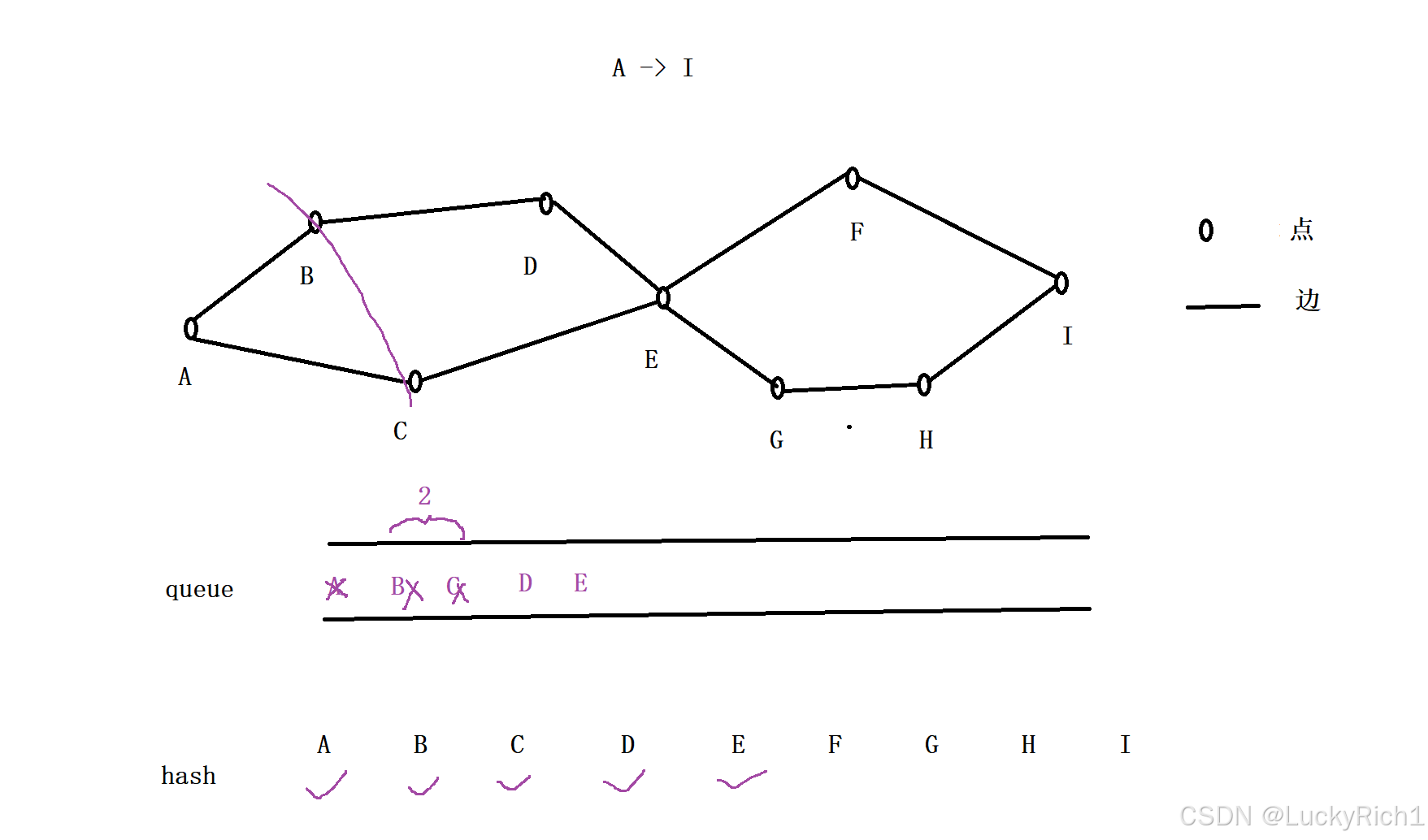
接下来重要的来了，我们会先统计队列中有多少元素，然后同时把队列中元素都弹出去。但是还是有一个先后，所以先弹B，在弹C。我们是在一个循环中进行的，依次把这两个元素都弹出，意思就是把刚刚扩展出来的这一层在同一时间在向外扩展一层。

总结一下：弹出元素之前，先统计队列中有多少元素，然后循环把当前队列中的元素弹出，然后把与其相连的地方加入队列。

这两者虽然有先后，但是在我们看来是同时往外扩展的。

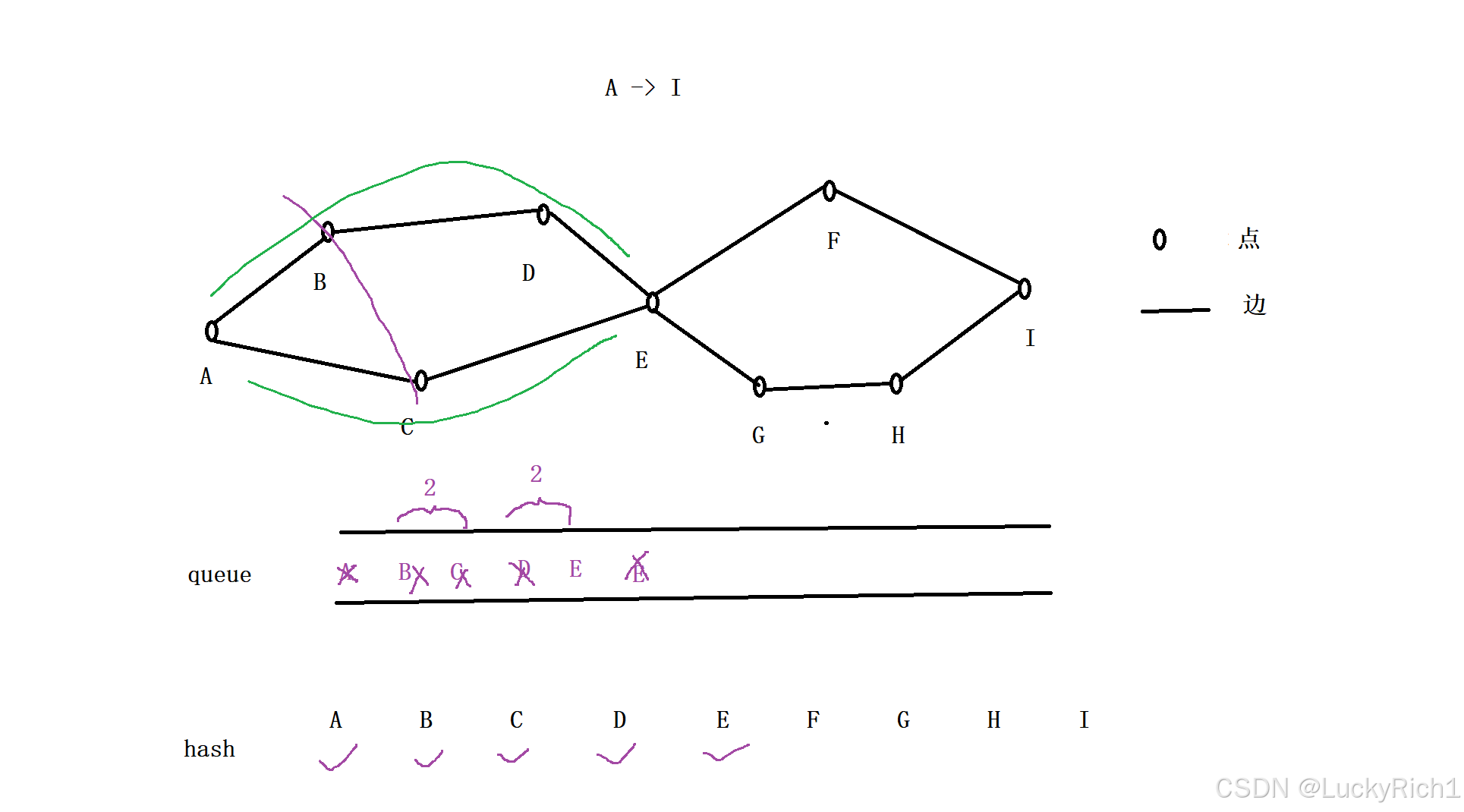
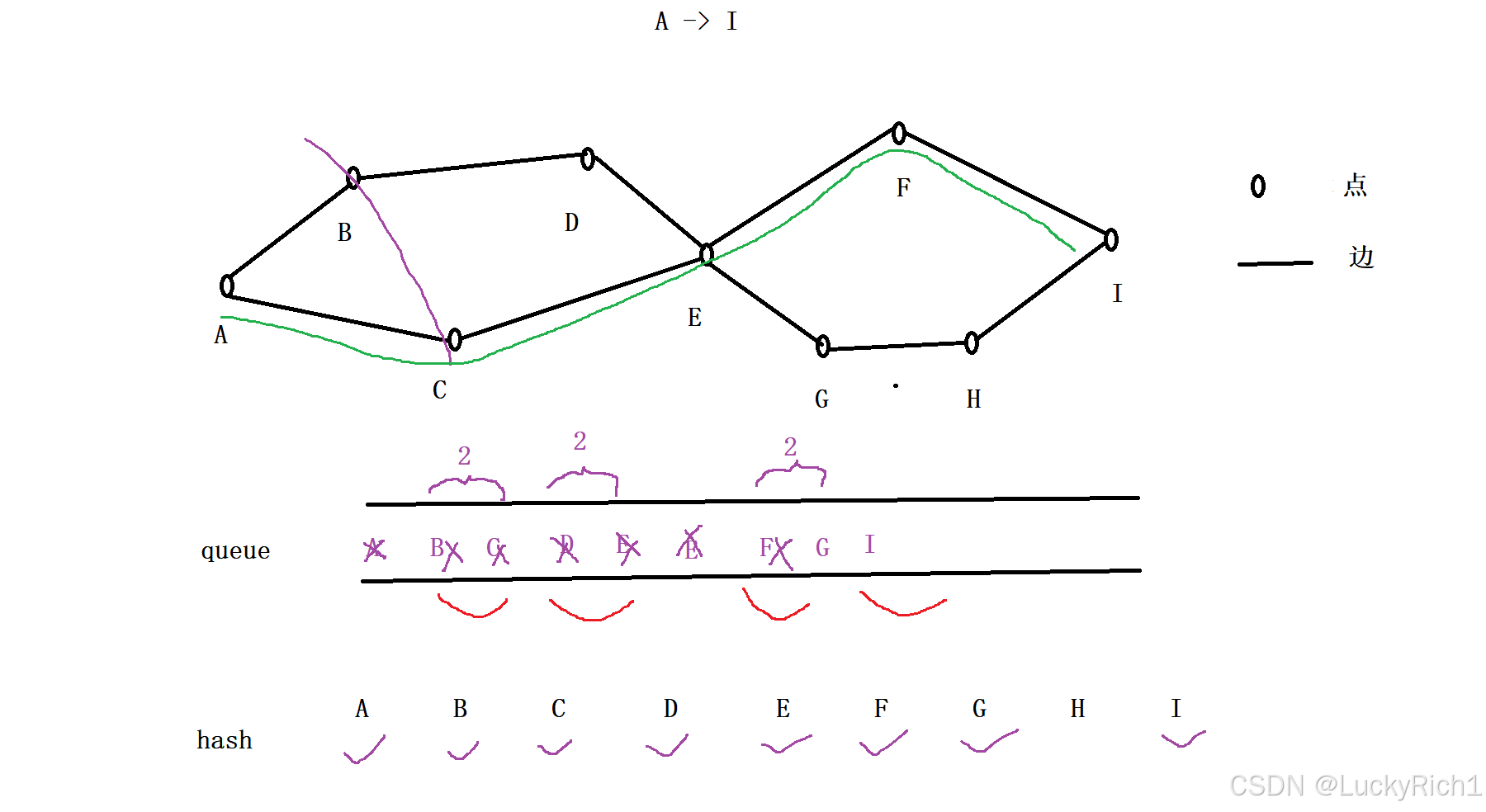
接下来也是这样的操作，我们先把D弹出，把D能相连的地方加进来，但是扩展D的时候，发现E已经加入到队列中，此时就不需要把E加入到队列中了。

因为这块在把后来的E加进来后面路径和之前加入的队列的E走的是一样的，而且这个后来的E加了之后也不是最优解，因为之前发现一条路到E了，而此时你的E是后过来的，那你的路径就是比我长，肯定不是最优解。

所以需要一个数组或者hash来标记当前位置是否被访问过。

到E的时候把和E相连的地方加入队列。

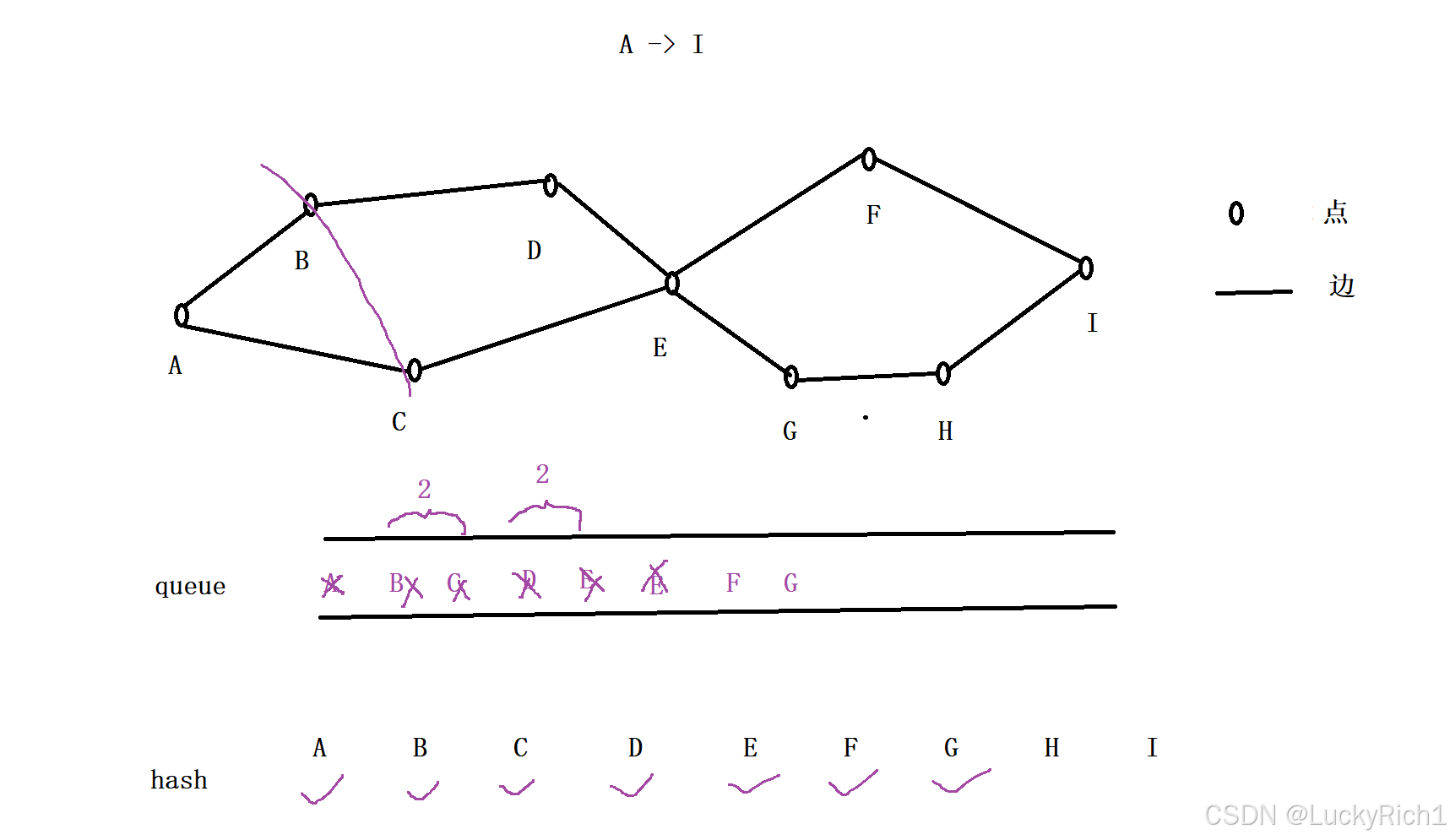
然后重复刚才的过程，统计队列中的元素个数，然后把F弹出去的时候会把I加入队列，把G弹出去的时候把H加入队列，但是这一步不用做了。因为把F弹出把I加入队列此时我们就已经找到终点了，后面的过程就不用进行了。我们此时已经找到最短路径了。那就是从 A -> C -> E -> F -> I。

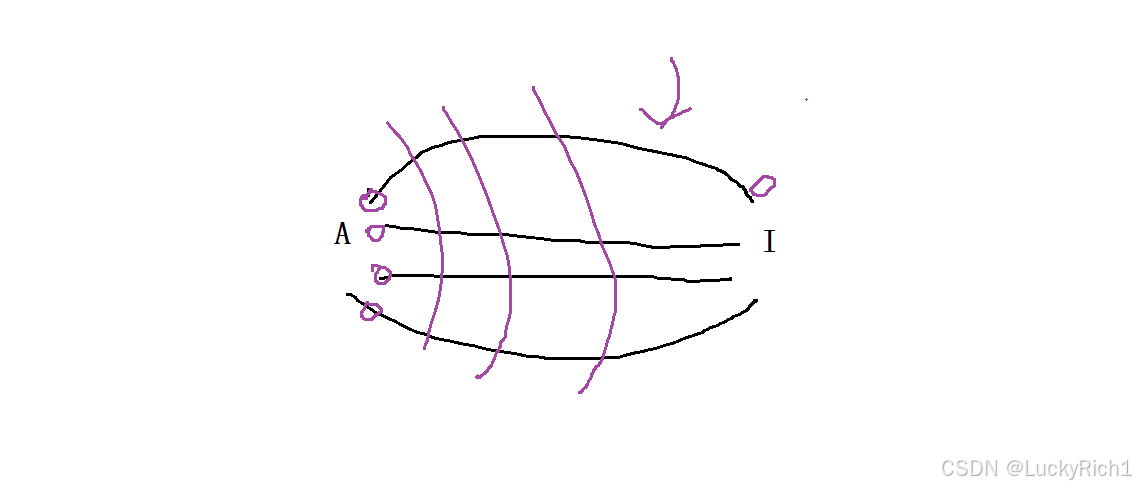
接下来感性的证明一下为什么 BFS 能够找到最短路径，为什么一层一层往外拨开第一次碰到终点就说找到最短路径了呢？

从 A 到 I 其实有特别多的路，我们层序遍历的过程相当于有很多小人在A起点同时出发同时每次向后移动一个单位，原因在于我们边的权值都是一样的。当我们发现一个小人以最快的速度到达 I 这个位置，那绝对是最优的。原因就是每个人每一次移动的时候路程是相等的、速度是相等的、时间是相等的，所以最先到达 I 位置，这条路径就是最优路径。

这种问题一般都是问 最短路径是多少？ 那如何找出最短路径是多少呢？

这里我们发现，你扩展层数是多少你的最短路径就是多少。

比如说从A扩展到B、C 这是一层，从B、C扩展到D、E 又是一层，从D、E扩展到F、G 又一层，从F、G扩展到 I 又是一层，总共扩展四层，因此最短路径是4。

所以可以搞一个变量，每扩展一层就++一下。当第一次扩展到 I 的时候停止，返回这个变量就可以了。

2.迷宫中离入口最近的出口

题目链接：1926. 迷宫中离入口最近的出口

题目分析：

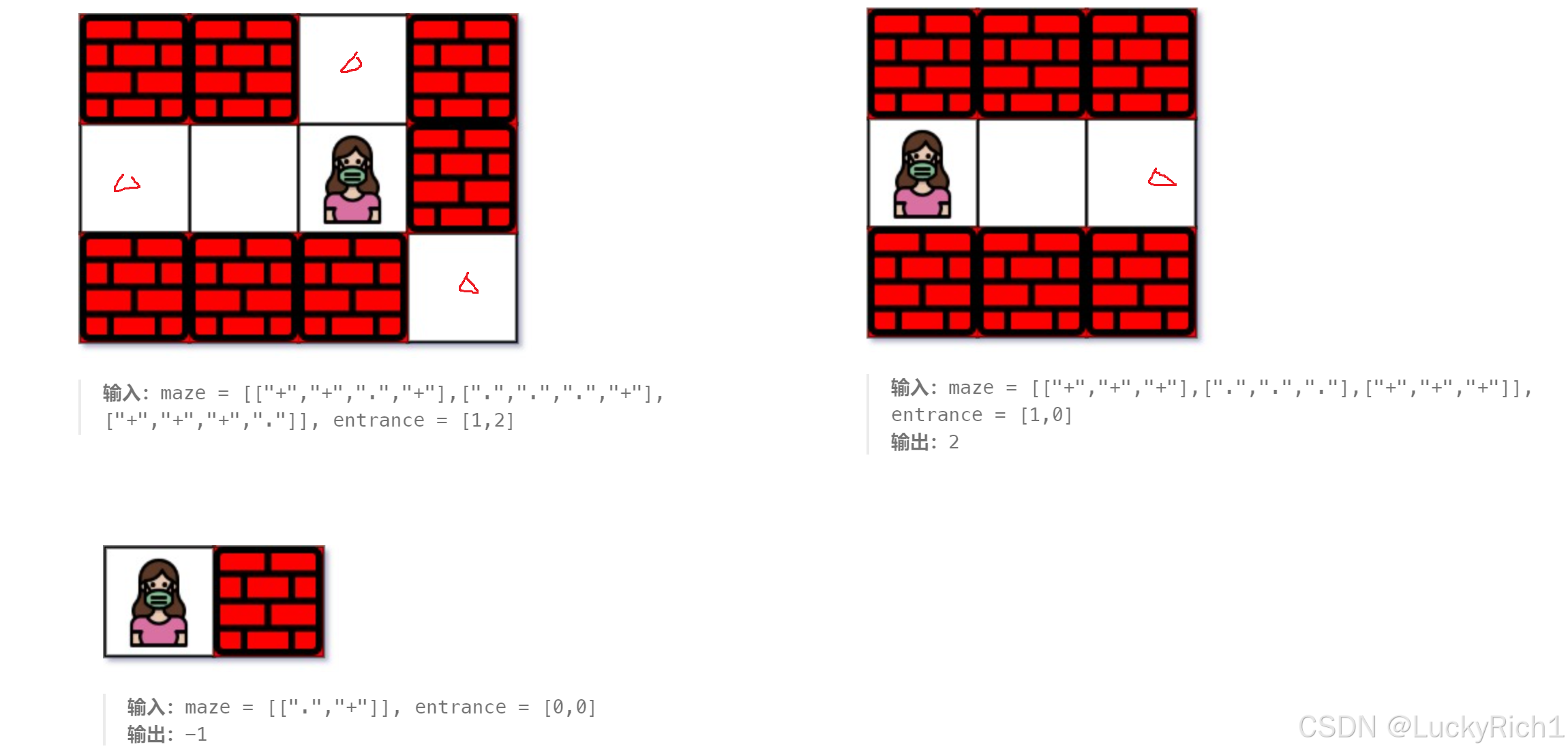
给你一个 m x n 的迷宫矩阵 maze （下标从 0 开始），矩阵中有空格子（用 ‘.’ 表示）和墙（用 ‘+’ 表示）。同时给你迷宫的入口 entrance ，用 entrance = [entrancerow, entrancecol] 表示你一开始所在格子的行和列，你可以上下左右四个方向移动，让你找到离你刚开始所在位置最近的出口并且返回路径。这里的出口就是在maze边界上的空格子。注意刚开始的位置即使就是在maze边界上的空格子上也不能算作出口。如果不存在路径返回-1.

算法原理：

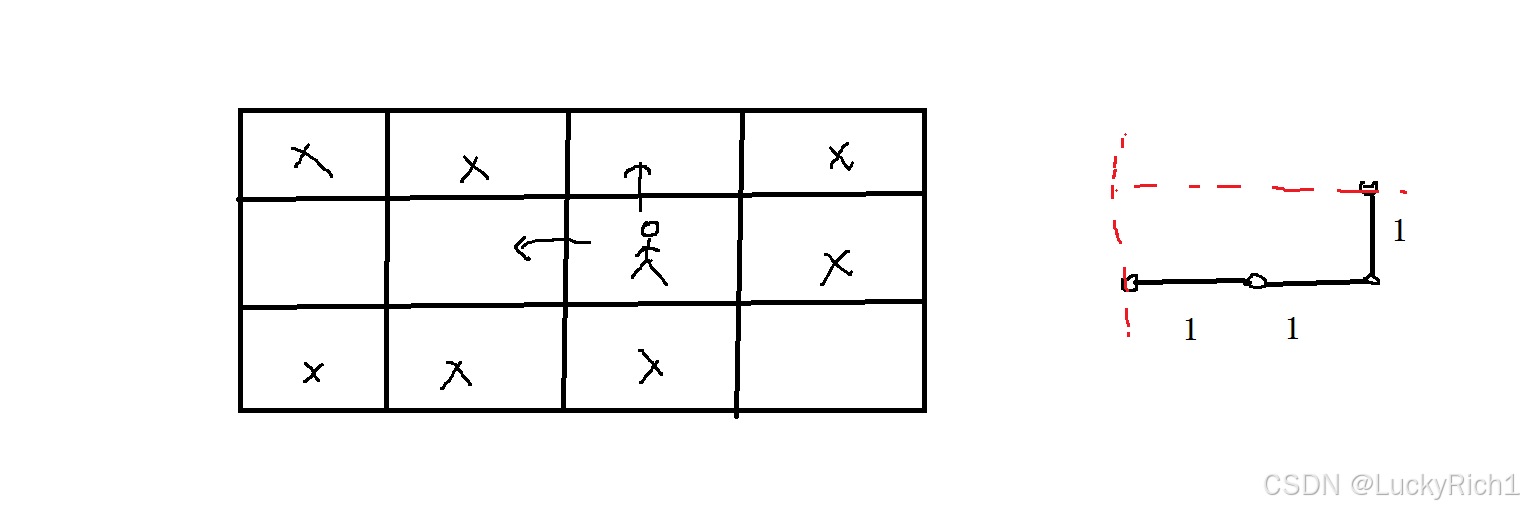
以第一个例子为例，刚开始这个小人可以向上走也可以向左走，如果把小人抽象成点的话，此时把点连成线，会发现每次都只走一步。会发现权值都是1，所以这个问题就可以转换成 边权为1的最短路径问题。从开始点出发到边界上的点最短路径是多少。

边权为 1 的最短路径问题

解法：BFS
如何解决前面已经说的非常详细了。把刚开始位置加入队列，然后一层一层往外扩，直到扩展到边界上的点为止。返回扩展的层数即可。注意还要搞一个二维数组用来标记当前为止是否已经被访问过了。

class Solution {
    bool vis[101][101]={0};
    int dx[4] = {0, 0, 1, -1};
    int dy[4] = {1, -1, 0, 0};
public:
    int nearestExit(vector<vector<char>>& maze, vector<int>& e) {

        int m = maze.size(), n = maze[0].size();
        queue<pair<int,int>> q;
        q.push({e[0],e[1]});
        vis[e[0]][e[1]] = true;
        int step = 0;
        while(q.size())
        {
            ++step;
            int sz = q.size();
            for(int i = 0; i < sz; ++i)
            {
                auto [a, b] = q.front();
                q.pop();
                for(int k = 0; k < 4; ++k)
                {
                    int x = a + dx[k], y = b + dy[k];
                    if(x >= 0 && x < m && y >= 0 && y < n && maze[x][y] == '.' && !vis[x][y])
                    {               
                        if(x == 0 || x == m-1 || y == 0 || y == n-1) return step;
                        q.push({x,y});
                        vis[x][y] = true;
                    }
                }  
            }

        }
        return -1;//层序遍历结束之后还没有找到出口,返回-1
    }
};

3.最小基因变化

题目链接： 433. 最小基因变化

题目分析：

基因序列可以表示为一条由 8 个字符组成的字符串，其中每个字符都是’A’、‘C’、‘G’ 和 ‘T’ 之一。求从基因序列 start 变为 end 所发生的有效的基因变化并且是最小的。有效的基因变化指的是start每次基因变化如果都是在基因库 bank 里就是有效的。一次基因变化就意味着这个基因序列中的一个字符发生了变化。例如，“AACCGGTT” --> “AACCGGTA” 就是一次基因变化。

算法原理：

先把这到题转为为之前遇到的关于图论问题中的， 边权为 1 的最短路径问题。

给一个起始的基因序列，给一个终止的基因序列，想把这个起始基因序列转化为终止的基因序列。在转化过程中要求每次转化只能改变基因序列中其中一个字符并且只能从"A",“C”,“G”,"T"中任取一个字符。

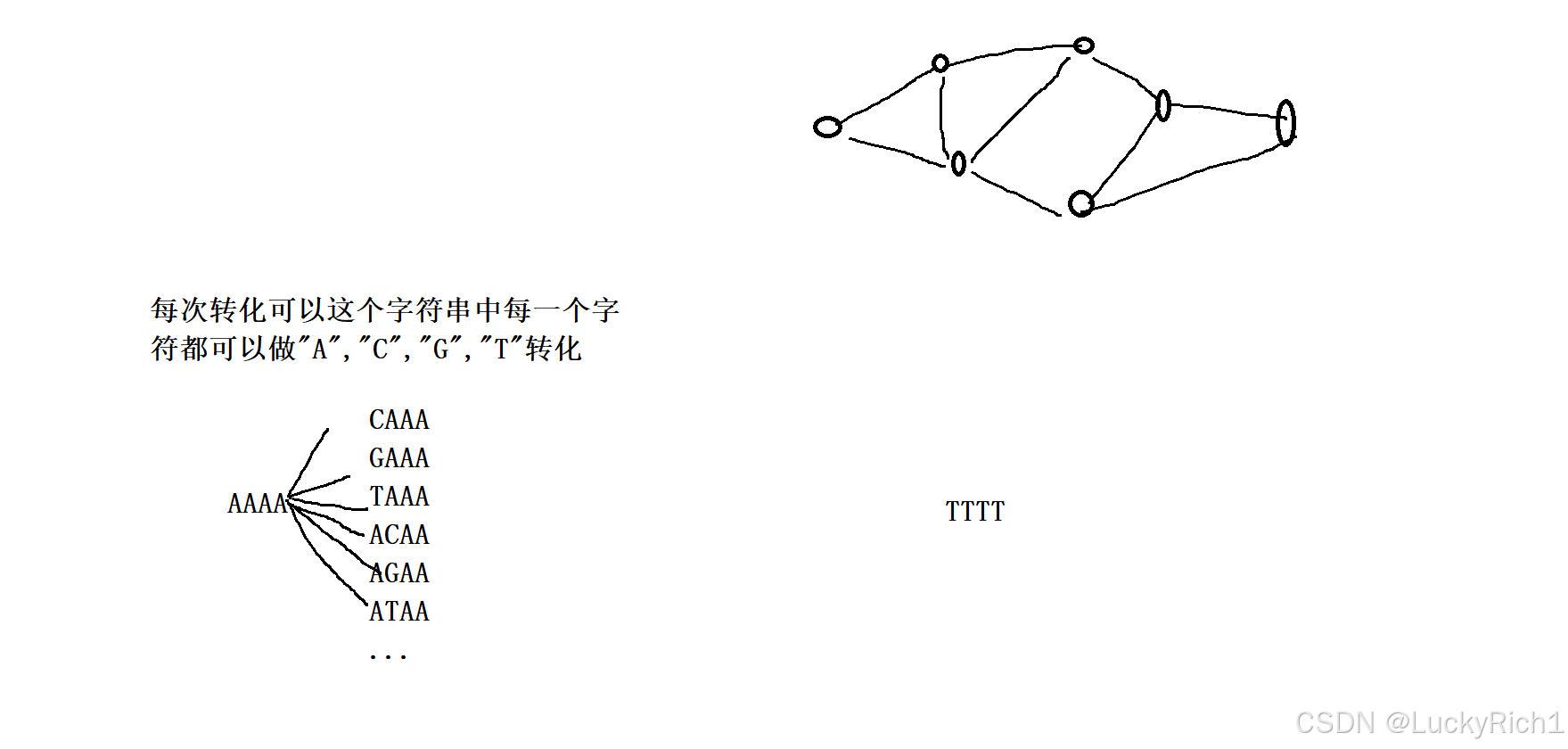
如果把一个一个字符串抽象出图论中一个个点，那这个问题不就变成了，给一个起始位置和一个终止位置，中间有一些变化的的过程，问起始位置到终点位置最短路径是多少，这问题不就完美的抽象成图论问题吗。并且每次都是一步变化，因此就转变成 边权为 1 的最短路径问题。

接下来就是细节问题：

肯定要创建一个队列，队列里存的是一个个字符串。而且还需要一个东西来标记当前字符串已经被搜索过了。原因是CAAA 继续向外扩展会回到AAAA这就有问题了，因此需要标记字符串已经被搜索。这里不能在用数组了，我们用hash表存一个个字符串。

1. 用哈希表来标记搜索过的状态
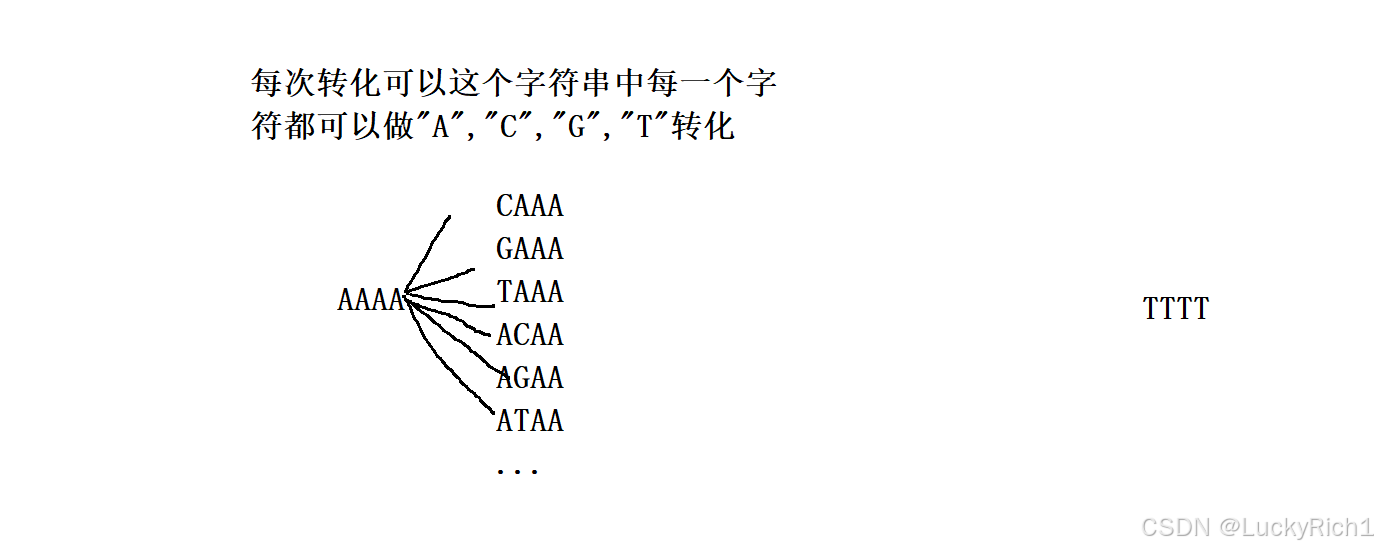
2. 如何枚举出当前这一次所有变化情况呢？

很简单搞一个for循环，对字符串中每一个字符遍历依次，并且每一个字符都按顺序修改成"A",“C”,“G”,“T”。这样就枚举出当前这一次所有变化情况。遍历字符串中每一个位置然后每一个位置都修改四次！而且因为我们前面有哈希表标记搜索过的状态因此不会有重复的情况，不用在判断一次当前字符串和前面字符串是否相等在修改，如 CAAA -> AAAA，因为AAAA已经被标记过搜索了，所以不用特殊判断。

3. 枚举出来的所有情况，都需要加入到队列里面吗？

并不需要，只需要把枚举出来并且在基因库bank里面的才加入到队列。

4. 如何快速判断是否在基因库中存在

把基因库中的字符串加入到hash表。此时枚举出来的字符串就可以在这个hash表找一下就可以。

class Solution {
public:
    int minMutation(string startGene, string endGene, vector<string>& bank) {

        unordered_set<string> hash(bank.begin(),bank.end());// 存储基因库里面的基因序列
        unordered_set<string> vis; // ⽤来标记已经搜索过的状态
        
		if(startGene == endGene) return 0;
 		if(!hash.count(endGene)) return -1;
 		
        queue<string> q;
        q.push(startGene);
        vis.insert(startGene);
        int step = 0;
        string change = "ACGT";
        while(q.size())
        {
            step++;
            int n = q.size();
            while(n--)
            {
                string t = q.front();
                q.pop();
                for(int i = 0; i < 8; ++i)
                {
                    string tmp = t;//细节问题,我们只是修改字符串的一个字符,下一次还想在原始字符串中修改下一个字符
                    for(int j = 0; j < 4; ++j)
                    {
                        tmp[i] = change[j];
                        if(hash.count(tmp) && !vis.count(tmp))
                        {
                            if(tmp == endGene) return step;
                            q.push(tmp);
                            vis.insert(tmp);
                        } 
                    }
                }
            }

        }
        return -1;
    }
};

4.单词接龙

题目链接：127. 单词接龙

题目分析：

给一个起始单词给一个终止单词求起始单词转化为终止单词 最短转换序列 中的 单词数目 。如果不存在这样的转换序列，返回 0 。这道题和上面几乎是一模一样，唯一不一样的就是求得是最短转换序列 中的 单词数目 。转化规则还是每次遍历字符串中每一个位置，每一个位置都可以 从 ‘a’~‘z’ 中按照顺序改变，但是不是盲目改变，改变之后得字符串必须在wordList字典中存在才行。才属于一次有效改变。

算法原理：

和最小基因序列几乎一模一样，不过就换成了每个位置从 ‘a’ ~ ‘z’ 中选，而且最终返回的是 最短转换序列 中的 单词数目 ，因此第一个进入队列的也要算上。

class Solution {
public:
    int ladderLength(string beginWord, string endWord, vector<string>& wordList) {

        unordered_set<string> hash(wordList.begin(),wordList.end());
        unordered_set<string> vis;// ⽤来标记已经搜索过的状态

        if(!hash.count(endWord)) return 0;
        
        queue<string> q;
        q.push(beginWord);
        vis.insert(beginWord);
        int ret = 1;
        while(q.size())
        {
            ret++;
            int n = q.size();
            while(n--)
            {
                string t = q.front();
                q.pop();
                for(int i = 0; i < t.size(); ++i)
                {
                    string tmp = t;
                    for(char ch = 'a'; ch <= 'z'; ++ch)
                    {
                        tmp[i] = ch;
                        if(hash.count(tmp) && !vis.count(tmp))
                        {
                            if(tmp == endWord) return ret;
                            q.push(tmp);
                            vis.insert(tmp);
                        }
                    }
                }
            }
        }
        return 0;
    }
};

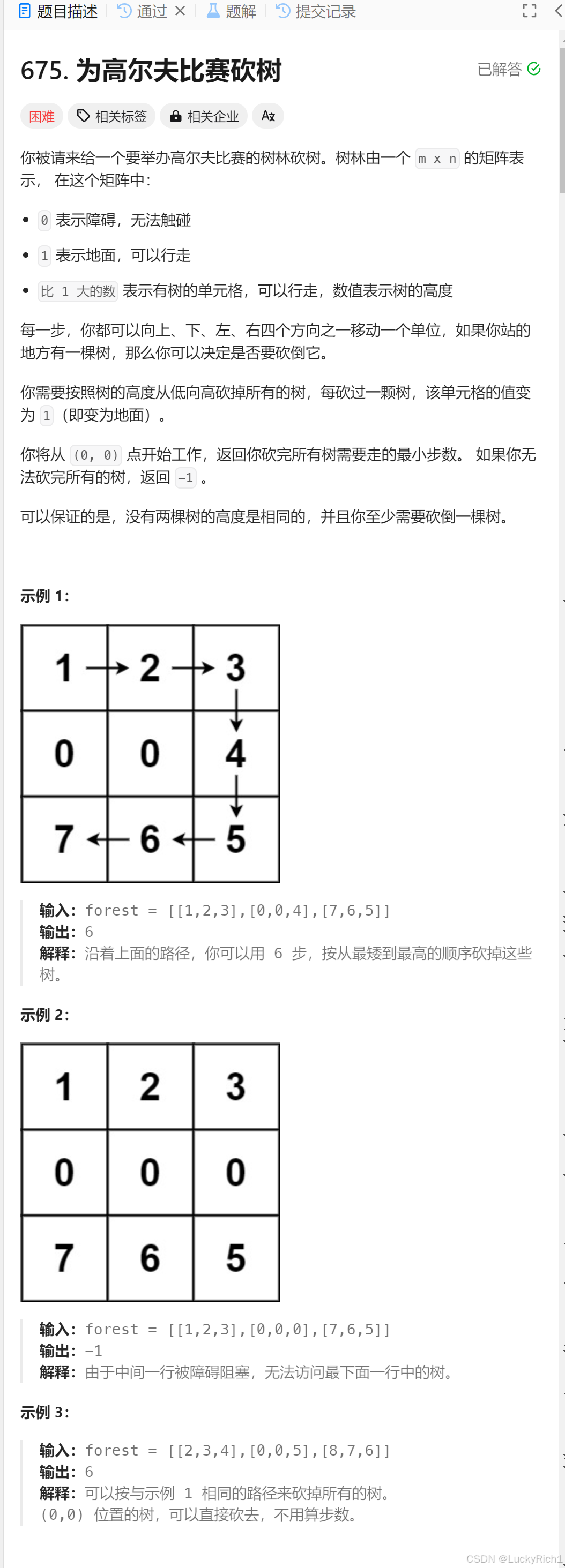
4.为高尔夫比赛砍树

题目链接： 675. 为高尔夫比赛砍树

题目分析：

给一个mxn的矩阵，

0 表示障碍，无法触碰
1 表示地面，可以行走
比 1 大的数 表示有树的单元格，可以行走，数值表示树的高度

每一步，你都可以向上、下、左、右四个方向之一移动一个单位，如果你站的地方有一棵树，那么你可以决定是否要砍倒它。

你需要按照树的高度从低向高砍掉所有的树，每砍过一颗树，该单元格的值变为 1（即变为地面）。

你将从 (0, 0) 点开始工作，返回你砍完所有树需要走的最小步数。 如果你无法砍完所有的树，返回 -1 。

算法原理：

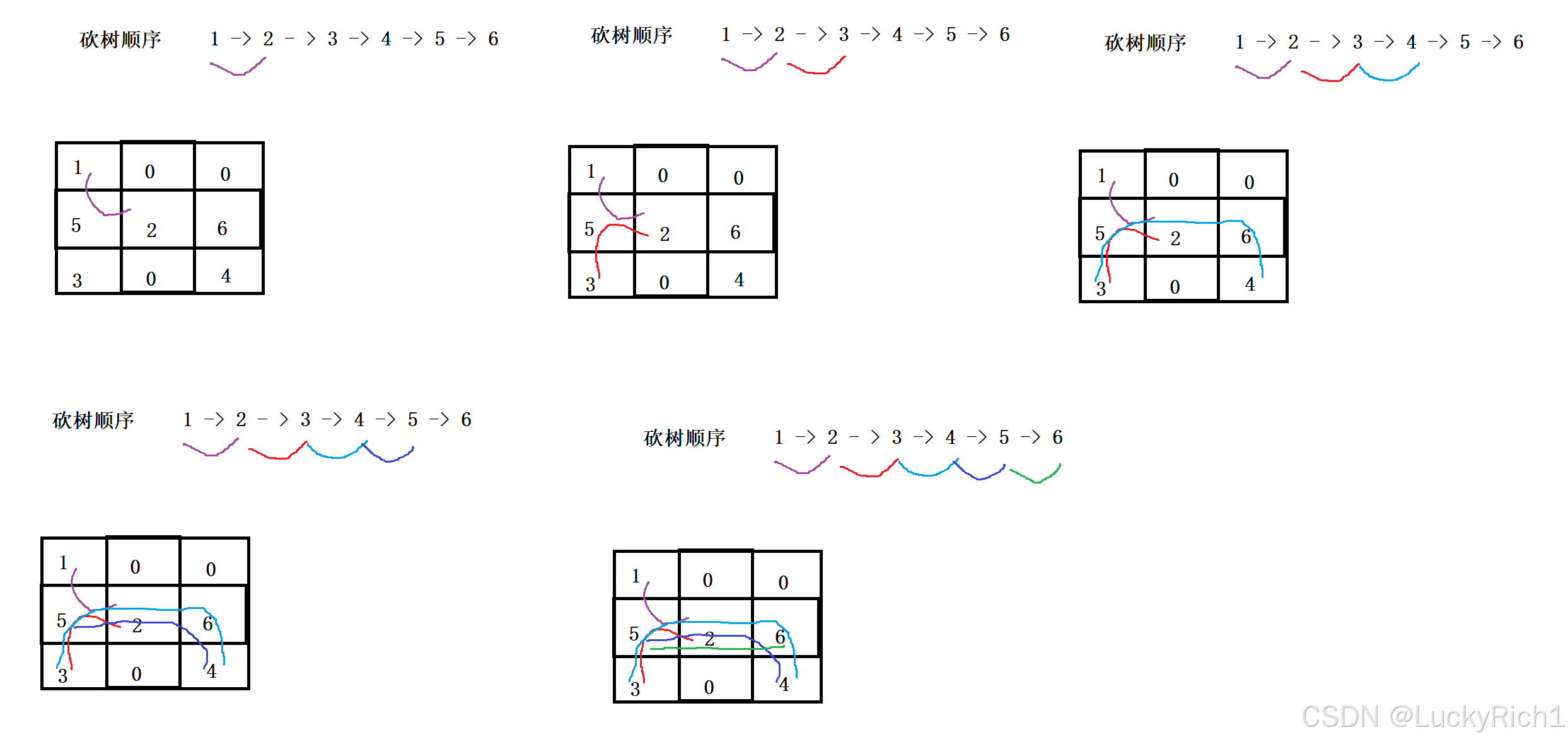
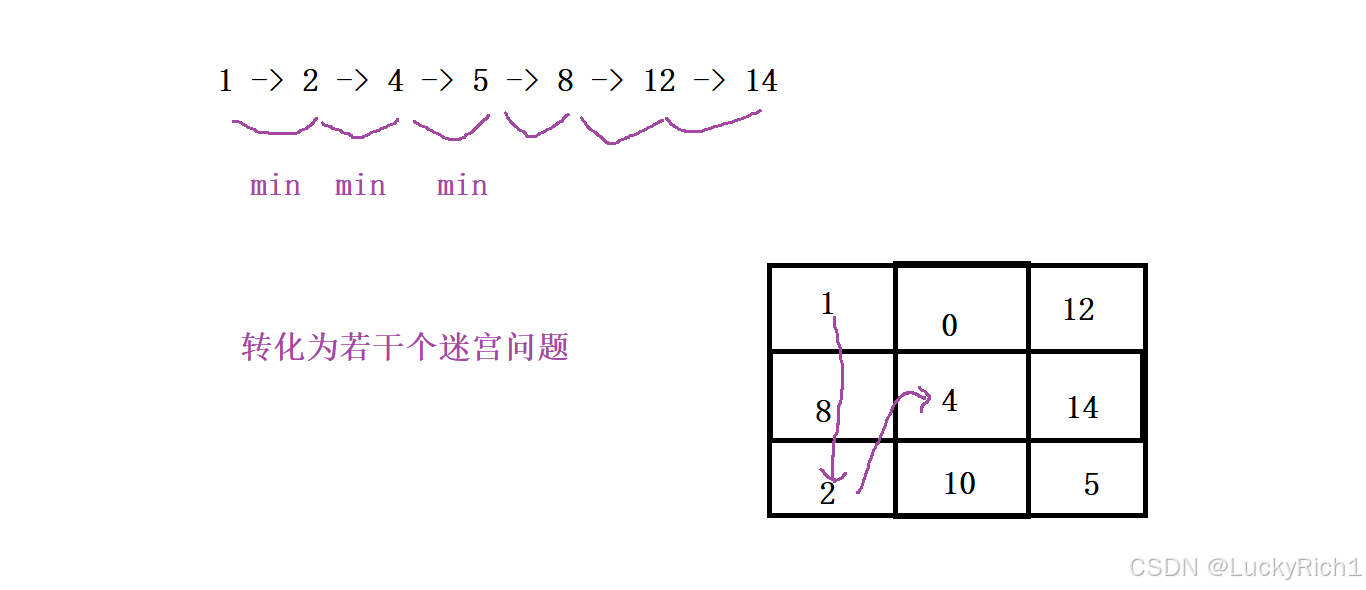
当我们把题意搞清楚，我们知道砍树不能随便砍，必须按照从底到高顺序来砍，因此我们必须先想办法把下标中的树先按照从低到高排下序，然后从(0,0)开始砍。此时这个问题就转化为，1->2 只要知道1->2最短距离不就可以了吗，然后就可以砍2号树。在然后从 2->4，只要知道2->4最短距离然后就可以砍4号树。。。。 这不就变成了若干个迷宫问题了吗。然后把所有最短距离加起来就行了。

那如何先对树进行一下排序把砍树的顺序找到呢？
可以先用数组把所有待砍树的下标保存起来，然后根据下标所对应的值对下标进行排序。

class Solution {
    int m,n;
public:
    int cutOffTree(vector<vector<int>>& f) 
    {
        m = f.size(), n = f[0].size();
        // 1. 准备⼯作：找出砍树的顺序
        vector<pair<int, int>> trees;
        for(int i = 0; i < m; i++)
            for(int j = 0; j < n; j++)
                if(f[i][j] > 1) trees.push_back({i, j});
        
        sort(trees.begin(), trees.end(), [&](const pair<int, int>& p1, const pair<int, int>& p2)
        {
            return f[p1.first][p1.second] < f[p2.first][p2.second];
        });

        // 2. 按照顺序砍树
        int bx = 0, by = 0;
        int ret = 0;
        for(auto& [a, b] : trees)
        {
            int step = bfs(f, bx, by, a, b);
            if(step == -1) return -1;
            ret += step;
            bx = a, by = b;
        }
        return ret;
    }

    bool vis[51][51];
    int dx[4] = {0, 0, 1, -1};
    int dy[4] = {1, -1, 0, 0};
    
    int bfs(vector<vector<int>>& f, int bx, int by, int ex, int ey)
    {
        if(bx == ex && by == ey) return 0;
        queue<pair<int, int>> q;
        memset(vis, 0, sizeof vis); // 清空之前的数据
        q.push({bx, by});
        vis[bx][by] = true;
        int step = 0;
        while(q.size())
        {
            step++;
            int sz = q.size();
            while(sz--)
            {
                auto [a, b] = q.front();
                q.pop();
                for(int i = 0; i < 4; i++)
                {
                    int x = a + dx[i], y = b + dy[i];
                    if(x >= 0 && x < m && y >= 0 && y < n && f[x][y] && !vis[x][y])
                    {
                        if(x == ex && y == ey) return step;
                        q.push({x, y});
                        vis[x][y] = true;
                    }
                }
            }
        }
        return -1;
    }