一、数据简介及分析
本项目使用的数据是有关葡萄牙银行机构的直接营销活动(电话)。分类目标是预测客户是否会订阅定期存款(变量y)。
这是一个多维数据,有20维数据。
数据解释如下:
分类目标是预测客户是否会认购(是/否)定期存款(变量y)。
1 – age:年龄(数字)
2 - job:工作类型(分类:“管理员”、“蓝领”、“企业家”、“女佣”、“管理”、“退休”、“自雇”、“服务”、“学生”、“技术员”、“失业”、“未知”)
3 - marital:婚姻状况(分类:“离婚”,“已婚”,“单身”,“未知”;注:“离婚”是指离婚或丧偶)
4 – education:教育(分类:“基本.4y”、“基本.6y”、“基本.9y”、“高中”、“文盲”、“专业课程”、“大学学位”、“未知”)
5 - default:信用是否违约?(分类:“否”、“是”、“未知”)
6 - default:有住房贷款吗?(分类:“否”、“是”、“未知”)
7 - loan:有个人贷款吗?(分类:“否”、“是”、“未知”)
8 - contact:联系人通信类型(分类:“蜂窝”,“电话”)
9 - month:一年中的最后一个联系月份(分类:“一月”、“二月”、“三月”、“…”、“十一月”、“十二月”)
10 - day_of_week:一周中的最后一个联系日(分类:“周一”、“周二”、“周三”、“周四”、“周五”)
11 - duration:上次联系持续时间,以秒为单位(数字)。重要说明:此属性对输出目标有很大影响(例如,如果持续时间=0,则y=‘no’)。然而,在执行呼叫之前,持续时间是未知的。
12 - campaign:在此活动期间以及为此客户端执行的联系人数(数字,包括上次联系人)
13 - pdays:上次联系客户后经过的天数(数字;999 表示之前未联系过客户)
14 - previous: 此活动之前和为此客户端执行的联系人数(数字)
15 - poutcome:上一次营销活动的结果(分类:“失败”、“不存在”、“成功”)
16 - emp.var.rate:就业变化率 - 季度指标(数字)
17 - cons.price.idx:居民消费价格指数 - 月度指标(数字)
18 - cons.conf.idx:消费者信心指数 - 月度指标(数字)
19 - Euribor3M:欧洲同业拆借利率3个月利率 - 每日指标(数字)
20 - nr.employed:员工数量-季度指标(数字)
21 - y :客户是否认购了定期存款?(二进制:“是”,“否”)
初步观察总体数据为4115条,其中有3667条分类为”no”的数据,448条分类结果为”yes”。其中连续数据:age、duration、campaign、pdays、emp.var.rate、cons.price.idx、cons.conf.idx、Euribor3M、nr.employed,这些连续数据需要进行分段处理。分类结果为“yes”只出现在Duration大于等于63。分类结果为“yes”只出现在campaign小于等于11。
二、集成器设计思路
1. 个体学习器的选择
1.1个体学习器简介
本实验个体学习器采用决策树算法。决策树(decision tree)是一种基本的分类与回归方法。其主要优点是模型具有可读性,分类速度快。学习时利用训练数据,根据损失函数最小化的原则建立决策树。预测时,对新的数据利用决策树模型进行分类。
决策树通常包括三个步骤:特征选择、决策树的生成、决策树的修剪,其中决策树的生成只考虑局部最优,决策树的修剪则考虑全局最优。
1.2个体学习器建立过程
决策树的生成是一个递归过程。在决策树基本算法中,有三种情形会导致递归返回:(1)当前结点包含的样本全属于同一类别,无需划分;(2)当前属性集为空,或是所有样本在所有属性上取值相同,无法划分;(3)当前结点包含的样本集合为空,不能划分。
在第(2)种情形下,我们把当前结点标记为叶结点,并将其类别设定为该结点所含样本最多的类别;在第(3)种情形下,同样把当前结点标记为叶结点,将其类别设定为其父结点所含样本最多的类别。注意这两种情形的处理实质个同:情形(2)是在利用当前结点的后验分布,而情形(3)则是把父结点的样本分布作为当前结点的先验分布。
2.个体学习器训练方法
2.1随机森林简介
随机森林(Random Forest,简称RF) [Breiman, 2001a]是Bagging的一个扩展变体。 RF在以决策树为基学习器构建Bagging集成的基础上,进一步在决策树的训练过程中引入了随机属性选择。具体来说,传统决策树在选择划分属性时是在当前结点的属性集合(假定有d个属性)中选择一个最优属性;而在RF中,对基决策树的每个结点,先从该结点的属性集合中随机选择一个包含k个属性的子集,然后再从这个子集中选择一个最优属性用于划分,这里的参数k控制了随机性的引入程度:若令k=d,则基决策树的构建与传统决策树相同;若令k=1,则是随机选择一个属性用于划分;一般情况下,推荐值k=log2d。
2.2随机森林优点
随机森林简单、容易实现、计算开销小,它在很多现实任务中展现出强大的性能,被誉为“代表集成学习技术水平的方法”。随机森林对Bagging只做了小改动,但是与Bagging中基学习器的“多样性”仅通过样本扰动(通过对初始训练集采样)而来不同,随机森林中基学习器的多样性不仅来自样本扰动,还来自属性扰动,这就使得最终集成的泛化性能可通过个体学习器之间差异度的增加而进一步提升。
2.3随机森林特点
随着学习器数目的增加,随机森林通常会收敛到更低的泛化误差值得一提的是, 随机森林的训练效率常优于Bagging,因为在个体决策树的构建过程中,Bagging使用的是“确定型”决策树,在选择划分属性时要对结点的所有属性进行考察,而随机森林使用的“随机型”决策树则只需考察一个属性子集。
2.4参数选择
每次随机选择属性个数k=log2d≈4
个体学习器数量n=10
3.结合策略
3.1投票法
对分类任务来说,学习器hi将从类别标记集合{1,… }中预测出一个标记,最常见的结合策略是使用投票法(voting)。我们将h在样本x上的预测输出表示为一个N维向量,其中的(x)是hi在类别标记C;上的输出。
- 绝对多数投票法(majority voting)
即若某标记得票过半数,则预测为该标记;否则拒绝预测。 - 相对多数投票法(plurality voting)
即预测为得票最多的标记,若同时有多个标记获最高票,则从中随机选取一个。 - 加权投票法(weighted voting)
本实验采用相对多数投票法进行个体学习器的结合。
三、实验结果及分析
1.集成学习器泛化能力评价
1.1留出法
“留出法”(hold-out)直接将数据集D划分为两个互斥的集合,其中一个集合作为训练集S,另一个作为测试集T,即D=SUT、S∩T=0。在S上训练出模型后,用T来评估其测试误差,作为对泛化误差的估计。
以二分类任务为例,假定D包含1000个样本,将其划分为S包含700个样本,T包含300个样本,用S进行训练后,如果模型在T上有90个样本分类错误,那么其错误率为(90/300)×100%=30%,相应的,精度为1-30%=70%。
集成学习器正确率:
0.9826086956521739
由软件进行决策树形成后,预测出的结果正确率为98%,可以得出集成学习器的泛化能力十分优秀了。
2.集成多样性评价
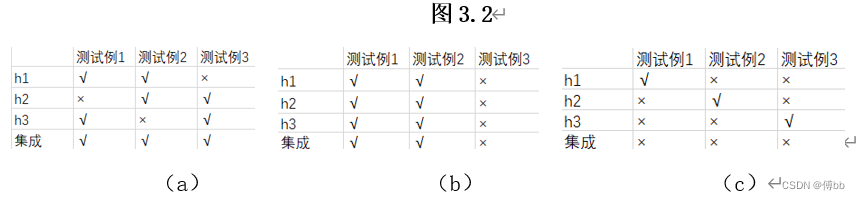
在二分类任务中,假定三个分类器在三个测试样本上的表现如图3.2所示,其中v表示分类正确,x表示分类错误,集成学习的结果通过投票法(voting)产生,即“少数服从多数”。在图3.2(a)中,每个分类器都只有66.6%的精度,但集成学习却达到了100%; 在图3.2(b)中,三个分类器没有差别,集成之后性能没有提高;在图3.2©中,每个分类器的精度都只有33.3%,集成学习的结果变得更糟。这个简单的例子显示出:要获得好的集成,个体学习器应“好而不同”,即个体学习器要有一定的“准确性”,即学习器不能太坏,并且要有“多样性”(diversity),即学习器间具有差异。
10个个体学习器的测试集预测结果见附录2:
预测结果中有一个测试集结果全为0,表明其对应的个体学习器泛化性能十分差。
其它每个个体学习器预测结果准确率都适中。
学习器之间没有相似性,相互独立。
3.集成学习器提升效果的分析
- 10个个体学习器分别的测试集正确率:
0.591304347826087
0.6260869565217392
0.5478260869565217
0.6608695652173913
0.4608695652173913
0.5130434782608696
0.3652173913043478
0.0
0.5304347826086957
0.6086956521739131 - 集成学习器测试集正确率:
0.9826086956521739
个体学习器的准确率最高0.6608695652173913,最低为0,10个个体学习器采用随机森林集成后,准确率提升到0.98,接近1,所以集成学习提升了学习效果,学习器泛化能力变好了。 - 集成学习分类结果真假列表:
[True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, False, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True] - 只有一个分类错误了,集成学习提升效果十分显著。
四、代码
import pandas as pd
import numpy as np
import pandas as pd
f=pd.read_csv('D:\\Users\\fuwei\\Desktop\\bank-additional\\bank-additional.csv',encoding='gbk')
f.drop(labels=['age','duration','campaign','pdays','emp.var.rate','cons.price.idx','cons.conf.idx','euribor3m','nr.employed'],
axis=1,inplace=True)
f.head(5)
labels=f.columns.tolist()[:-1]
f = np.array(f) #先将数据框转换为数组
f = f.tolist() #其次转换为列表
f_train=f[:4000]
f_test=f[4000:]
# 信息熵
import math
def calcShannonEnt(dataSet):
numEntries = len(dataSet)
labelCounts = {}
for featVec in dataSet:
currentLabel = featVec[-1]
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
shannonEnt = 0.0
for key in labelCounts:
prob = float(labelCounts[key])/numEntries
shannonEnt -= prob*np.log2(prob)
return shannonEnt
ent=calcShannonEnt(f_train)
print(ent)
import copy
def splitDataSet(dataSet, axis, value):
retDataSet = [] #构建新矩阵
#对于数据集中的数据
data=copy.deepcopy(dataSet)
for featVec in data:
if featVec[axis] == value: #一旦发现特征与目标值一致
featVec.pop(axis)
reducedFeatVec=featVec
retDataSet.append(reducedFeatVec) #将去除了指定特征列的数据集放在retDataSet里
return retDataSet #返回划分后的数据集
# 信息增益
import random
def chooseFeature(totaldataSet,totallabels,chooselabels):
df=pd.DataFrame(data=totaldataSet,
columns=totallabels+['y'])
df=df[chooselabels]
dataSet = np.array(df) #先将数据框转换为数组
dataSet = dataSet.tolist() #其次转换为列表
return dataSet
def chooseBestFeatureToSplit(totaldataSet,totallabels):
if len(totallabels)>4:
chooselabels=random.sample(totallabels,4)
dataSet=chooseFeature(totaldataSet,totallabels,chooselabels)
else:
dataSet=totaldataSet
chooselabels=totallabels
numFeatures = len(dataSet[0])-1
baseEntropy = calcShannonEnt(dataSet)
bestInfoGain = 0.0;
bestFeature = -1
for i in range(numFeatures):
featList = [example[i] for example in dataSet]
uniqueVals = set(featList)
newEntroy = 0.0
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
prop = len(subDataSet)/float(len(dataSet))
newEntroy += prop * calcShannonEnt(subDataSet)
infoGain = baseEntropy - newEntroy
if(infoGain > bestInfoGain):
bestInfoGain = infoGain
bestFeature = i
feature=chooselabels[bestFeature]
bestFeature=totallabels.index(feature)
return bestFeature
# 构造决策树
import operator
def majorityCnt(classList):
classCount = {}
for vote in classList:
if vote not in classCount.keys():classCount[vote] = 0
classCount[vote] += 1
sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)#利用operator操作键值排序字典
return sortedClassCount[0][0]
#创建树的函数(使用随机森林)
def createTree(dataSet,labels):
classList = [example[-1] for example in dataSet]
if classList.count(classList[0]) == len(classList):
return classList[0]
if len(dataSet[0]) == 1:
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet,labels)
bestFeatLabel = labels[bestFeat]
myTree = {bestFeatLabel:{}}
del(labels[bestFeat])
featValues = [example[bestFeat] for example in dataSet]
uniqueVals = set(featValues)
for value in uniqueVals:
subLabels = labels[:]
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)
return myTree
Tree=[]
for i in range(10):
labels=['job', 'marital', 'education', 'default', 'housing', 'loan', 'contact', 'month', 'day_of_week', 'previous', 'poutcome', 'age_range', 'duration_range', 'campaign_range', 'pdays_range', 'emp.var.rate_range', 'cons.price.idx_range', 'cons.conf.idx_range', 'euribor3m_range', 'nr.employed_range']
Tree.append(createTree(f_train, labels))
print("样本数据决策树:")
print(Tree)
# 测试样本分类
def classify(inputtree,featlabels,testvec):
classlabel=0
firststr = list(inputtree.keys())[0]
seconddict = inputtree[firststr]
featindex = featlabels.index(firststr)
for key in seconddict.keys():
if testvec[featindex]==key:
if type(seconddict[key]).__name__=='dict':
classlabel=classify(seconddict[key],featlabels,testvec)
else:
classlabel=seconddict[key]
return classlabel
f_test=f[4000:]
f_test=np.array(f_test)
f_test_X=f_test[:,0:-1].tolist()
f_test_y=f_test[:,-1].tolist()
print(f_test_y)
labels=['job', 'marital', 'education', 'default', 'housing', 'loan', 'contact', 'month', 'day_of_week', 'previous', 'poutcome', 'age_range', 'duration_range', 'campaign_range', 'pdays_range', 'emp.var.rate_range', 'cons.price.idx_range', 'cons.conf.idx_range', 'euribor3m_range', 'nr.employed_range']
# 投票法决定最终分类结果
total_test=[]
for tree in Tree:
test=[]
for testvec in f_test_X:
test.append(classify(tree,labels,testvec))
correct=[f_test_y[i]==test[i] for i in range(len(test))]
correct_rate=correct.count(True)/len(correct)
print(correct_rate)
total_test.append(test)
total_test=np.array(total_test)
result=[]
for i in range(len(total_test[0])):
count_0=total_test[:,i].tolist().count(0)
count_y=total_test[:,i].tolist().count('yes')
count_n=total_test[:,i].tolist().count('no')
max_count=max([count_n,count_y,count_0])
index_max=[count_n,count_y,count_0].index(max_count)
result.append(['no','yes',0][index_max])
correct=[f_test_y[i]==result[i] for i in range(len(result))]
correct_rate=correct.count(True)/len(correct)
print('------------\n',correct_rate)
-
代码使用注意事项
由于随机森林原理是每次选的结点属性集为随机选择,所以使用本代码运行每次生成的决策树都有可能不同,这篇文章只采用一次代码运行结果作参考。 -
本代码将决策树生成过程、随机森林、投票法都包含在内,决策树和随机森林对于多分类结果普遍适用,投票法只针对二分类适用,如有需要可自行改正。
-
数据下载
本文所使用的数据已经上传在我的资源里,大家需要可以自行下载。